Hostname: page-component-6bb9c88b65-vmslq Total loading time: 0 Render date: 2025-07-25T18:27:40.465Z Has data issue: false hasContentIssue false
  • English
  • Français

A dynamical systems view of granular flow: from monoclinal flood waves to roll waves

Published online by Cambridge University Press:  23 April 2019

Dimitrios Razis ,
Giorgos Kanellopoulos  and
Ko van der Weele Open the ORCID record for Ko van der Weele [Opens in a new window]
Dimitrios Razis
Affiliation:
Department of Mathematics and Center for Research and Applications of Nonlinear Science, University of Patras, 26500 Patras, Greece
Giorgos Kanellopoulos
Affiliation:
Department of Mathematics and Center for Research and Applications of Nonlinear Science, University of Patras, 26500 Patras, Greece
Ko van der Weele*
Affiliation:
Department of Mathematics and Center for Research and Applications of Nonlinear Science, University of Patras, 26500 Patras, Greece
*
†Email address for correspondence: weele@math.upatras.gr
Get access Rights & Permissions [Opens in a new window]

Abstract

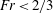On the basis of the Saint-Venant equations for flowing granular matter, we study the various travelling waveforms that are encountered in chute flow for growing Froude number. Generally, for $Fr<2/3$ one finds either a uniform flow of constant thickness or a monoclinal flood wave, i.e. a shock structure monotonically connecting a thick region upstream to a shallower region downstream. For 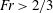$Fr>2/3$ both the uniform flow and the monoclinal wave cease to be stable; the flow now organizes itself in the form of a train of roll waves. From the governing Saint-Venant equations we derive a dynamical system that elucidates the transition from monoclinal waves to roll waves. It is found that this transition involves several intermediate stages, including an undular bore that had hitherto not been reported for granular flows.

JFM classification

Waves/Free-surface Flows: Channel flow Granular media: Granular media Nonlinear Dynamical Systems: Nonlinear Dynamical Systems

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 143 - 181
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media: Between Fluid and Solid. Cambridge University Press.Google Scholar
Aranson, I. S. & Tsimring, L. S. 2009 Granular Patterns. Oxford University Press.Google Scholar
Bagnold, R. A. 1966 The shearing and dilatation of dry sand and the ‘singing’ mechanism. Proc. R. Soc. Lond. A 295, 219–232.Google Scholar
Balmforth, N. J. & Mandre, S. 2004 Dynamics of roll waves. J. Fluid Mech. 514, 1–33.Google Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T 2015 Well-posed and ill-posed behaviour of the 𝜇(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Benjamin, T. B., Bona, J. L. & Mahony, J. J. 1972 Model equations for long waves in nonlinear dispersive systems. Phil. Trans. R. Soc. Lond. A 272, 47–78.Google Scholar
Bonneton, P., Filippini, A. G., Arpaia, L., Bonneton, N. & Ricchiuto, M. 2016 Conditions for tidal bore formation in convergent alluvial estuaries. Estuar. Coast. Shelf Sci. 172, 121–127.Google Scholar
Boudet, J. F., Amarouchene, B., Bonnier, B. & Kellay, H. 2007 The granular jump. J. Fluid Mech. 572, 413–431.Google Scholar
Bountis, T., van der Weele, K., Kanellopoulos, G. & Andriopoulos, K. 2011 Model reduction of a higher-order KdV equation for shallow water waves. In Coping with Complexity: Model Reduction and Data Analysis (ed. Gorban, E. N. & Roose, D.), Lecture Notes in Computational Science and Engineering, vol. 75, pp. 287–298. Springer.Google Scholar
Bresse, J. A. C. 1860 Cours de Mécanique Appliqué, Vol. II: Hydraulique. Mallet-Bachelier.Google Scholar
Chanson, H. 2011 Tidal Bores, Aegir, Eagre, Mascaret, Pororoca: Theory and Observations. World Scientific.Google Scholar
Daerr, A. & Douady, S. 1999 Two types of avalanche behaviour in granular media. Nature 399, 241–243.Google Scholar
Drazin, P. G. & Johnson, R. S. 1989 Solitons: An Introduction. Cambridge University Press.Google Scholar
Dressler, R. F. 1949 Mathematical solutions of the problem of roll waves in inclined open channels. Commun. Pure Appl. Maths 2, 149–194.Google Scholar
Duran, J. 2000 Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials. Springer.Google Scholar
Edwards, A. N. & Gray, J. M. N. T. 2015 Erosion-deposition waves in shallow granular free-surface flows. J. Fluid Mech. 762, 35–67.Google Scholar
Edwards, A. N., Viroulet, S., Kokelaar, B. P. & Gray, J. M. N. T 2017 Formation of levees, troughs and elevated channels by avalanches on erodible slopes. J. Fluid Mech. 823, 278–315.Google Scholar
Ferrick, M. G. 2005 Simple wave and monoclinal wave models: river flow surge applications and implications. Water Resour. Res. 41, W11402.Google Scholar
Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50.Google Scholar
Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.Google Scholar
Fowler, A. 2011 Mathematical Geoscience. Springer.Google Scholar
GDR-MiDi 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.Google Scholar
Gray, J. M. N. T., Tai, Y. C. & Noelle, S. 2003 Shock waves, dead-zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 491, 161–181.Google Scholar
Gray, J. M. N. T. & Ancey, C. 2009 Segregation, recirculation and deposition of coarse particles near two-dimensional avalanche fronts. J. Fluid Mech. 629, 387–423.Google Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged 𝜇(I)-rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503–534.Google Scholar
Jaeger, H., Nagel, S. & Behringer, R. 1996 Granular solids, liquids, and gases. Rev. Mod. Phys. 68, 1259–1275.Google Scholar
Johnson, C. G. & Gray, J. M. N. T 2011 Granular jets and hydraulic jumps on an inclined plane. J. Fluid Mech. 675, 87–116.Google Scholar
Kapitza, P. L. & Kapitza, S. P. 1949 Wave flow of thin layers of a viscous fluid. III. Experimental study of undulatory flow conditions. Zh. Eksp. Teor. Fiz. 19, 105–120 (translation in Collected Papers of P. L. Kapitza) ed. D. ter Haar, vol. II 1938–1964, pp. 690–709. Pergamon Press.Google Scholar
Köhler, A., McElwaine, J. N., Sovilla, B., Ash, M. & Brennan, P. 2016 The dynamics of surges in the 3 February 2015 avalanches in Vallée de la Sionne. J. Geophys. Res. Earth Surf. 121, 2192–2210.Google Scholar
Lagrée, P.-Y., Saingier, G., Deboeuf, S., Staron, L. & Popinet, S. 2017 Granular front for flow down a rough incline: about the value of the shape factor in depths averaged models. In Proceedings Powders & Grains 2017, EPJ Web of Conferences (ed. Radjai, F., Nezamadi, S., Luding, S. & Delenne, J. Y.), vol. 140, 03046. EDP Sciences, Les Ulis Cedex.Google Scholar
Le Méhauté, B. 1976 An Introduction to Hydrodynamics and Water Waves. Springer.Google Scholar
Mejean, S., Faug, T. & Einav, I. 2017 A general relation for standing normal jumps in both hydraulic and dry granular flows. J. Fluid Mech. 816, 331–351.Google Scholar
Moots, E. E. & Mavis, F. T. 1938 A Study in Flood Waves, vol. 14. University of Iowa Studies in Engineering.Google Scholar
Needham, D. J. & Merkin, J. H. 1984 On roll waves down an open inclined channel. Proc. R. Soc. Lond. A 394, 259–278.Google Scholar
Peregrine, D. H. 1966 Calculations of the development of an undular bore. J. Fluid Mech. 25, 321–330.Google Scholar
Pouliquen, O. 1999 Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11, 542–548.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 113–151.Google Scholar
Pudasaini, S. P. & Hutter, K. 2007 Avalanche Dynamics. Springer.Google Scholar
Razis, D., Edwards, A. N., Gray, J. M. N. T. & van der Weele, K. 2014 Arrested coarsening of granular roll waves. Phys. Fluids 26, 123305.Google Scholar
Razis, D., Kanellopoulos, G. & van der Weele, K. 2018 The granular monoclinal wave. J. Fluid Mech. 843, 810–846.Google Scholar
Roberts, A. J. 1994 A One-Dimensional Introduction to Continuum Mechanics. World Scientific Publications.Google Scholar
Rouse, H. & Ince, S. 1963 History of Hydraulics, Dover; Unabridged and corrected republication of the work first published by the Iowa Institute of Hydraulic Research, State University of Iowa, 1957.Google Scholar
Rousseaux, G., Mougenot, J. M., Chatellier, L., David, L. & Calluaud, M. 2016 A novel method to generate tidal-like bores in the laboratory. Eur. J. Mech. (B/Fluids) 55, 31–38.Google Scholar
Saingier, G., Deboeuf, S. & Lagrée, P.-Y. 2016 On the front shape of an inertial granular flow down a rough incline. Phys. Fluids 28, 053302.Google Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.Google Scholar
Shome, M. L. & Steffler, P. M. 2006 Flood plain filling by a monoclinal flood wave. J. Hydraul. Engng ASCE 132, 529–532.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. With Applications to Physics, Biology, Chemistry, and Engineering. Perseus Books.Google Scholar
Takahashi, T. 2014 Debris Flow: Mechanics, Prediction and Countermeasures, 2nd edn. CRC Press, Taylor and Francis.Google Scholar
Viroulet, S., Baker, J. L., Edwards, A. N., Johnson, C. G., Gjaltema, C., Clavel, P. & Gray, J. M. N. T. 2017 Multiple solutions for granular flow over a smooth two-dimensional bump. J. Fluid Mech. 815, 77–116.Google Scholar
Viroulet, S., Baker, J.L., Rocha, F.M., Johnson, C.G., Kokelaar, B.P. & Gray, J.M.N.T. 2018 The kinematics of bidisperse granular roll waves. J. Fluid Mech. 848, 836–875.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar