Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Walter, Ryan K.
Squibb, Michael E.
Woodson, C. Brock
Koseff, Jeffrey R.
and
Monismith, Stephen G.
2014.
Stratified turbulence in the nearshore coastal ocean: Dynamics and evolution in the presence of internal bores.
Journal of Geophysical Research: Oceans,
Vol. 119,
Issue. 12,
p.
8709.
Soontiens, Nancy
Stastna, Marek
and
Waite, Michael L.
2015.
Topographically generated internal waves and boundary layer instabilities.
Physics of Fluids,
Vol. 27,
Issue. 8,
Cortés, A.
Wells, M. G.
Fringer, O. B.
Arthur, R.S.
and
Rueda, F. J.
2015.
Numerical investigation of split flows by gravity currents into two-layered stratified water bodies.
Journal of Geophysical Research: Oceans,
Vol. 120,
Issue. 7,
p.
5254.
Moore, Christine D.
Koseff, Jeffrey R.
and
Hult, Erin L.
2016.
Characteristics of bolus formation and propagation from breaking internal waves on shelf slopes.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
260.
Walter, Ryan K.
and
Phelan, P. Joe
2016.
Internal bore seasonality and tidal pumping of subthermocline waters at the head of the Monterey submarine canyon.
Continental Shelf Research,
Vol. 116,
Issue. ,
p.
42.
Arthur, Robert S.
and
Fringer, Oliver B.
2016.
Transport by breaking internal gravity waves on slopes.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
93.
Masunaga, Eiji
Fringer, Oliver B.
Yamazaki, Hidekatsu
and
Amakasu, Kazuo
2016.
Strong turbulent mixing induced by internal bores interacting with internal tide‐driven vertically sheared flow.
Geophysical Research Letters,
Vol. 43,
Issue. 5,
p.
2094.
Xu, Chengzhu
Subich, Christopher
and
Stastna, Marek
2016.
Numerical simulations of shoaling internal solitary waves of elevation.
Physics of Fluids,
Vol. 28,
Issue. 7,
Rapaka, Narsimha R.
and
Sarkar, Sutanu
2016.
An immersed boundary method for direct and large eddy simulation of stratified flows in complex geometry.
Journal of Computational Physics,
Vol. 322,
Issue. ,
p.
511.
Dorostkar, Abbas
Boegman, Leon
and
Pollard, Andrew
2017.
Three‐dimensional simulation of high‐frequency nonlinear internal wave dynamics in Cayuga Lake.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 3,
p.
2183.
Maderich, Vladimir
Jung, Kyung Tae
Terletska, Kateryna
and
Kim, Kyeong Ok
2017.
Head-on collision of internal waves with trapped cores.
Nonlinear Processes in Geophysics,
Vol. 24,
Issue. 4,
p.
751.
Shao, Yun-Chuan
Hung, Chen-Yen
and
Chou, Yi-Ju
2017.
Numerical study of convective sedimentation through a sharp density interface.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
513.
Arthur, Robert S.
Koseff, Jeffrey R.
and
Fringer, Oliver B.
2017.
Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
169.
Masunaga, Eiji
Arthur, Robert S.
Fringer, Oliver B.
and
Yamazaki, Hidekatsu
2017.
Sediment resuspension and the generation of intermediate nepheloid layers by shoaling internal bores.
Journal of Marine Systems,
Vol. 170,
Issue. ,
p.
31.
Allen, Rachel M.
Simeonov, Julian A.
Calantoni, Joseph
Stacey, Mark T.
and
Variano, Evan A.
2018.
Turbulence in the presence of internal waves in the bottom boundary layer of the California inner shelf.
Ocean Dynamics,
Vol. 68,
Issue. 4-5,
p.
627.
la Forgia, Giovanni
Tokyay, Talia
Adduce, Claudia
and
Constantinescu, George
2018.
Numerical investigation of breaking internal solitary waves.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Hogg, Charlie A. R.
Egan, Galen C.
Ouellette, Nicholas T.
and
Koseff, Jeffrey R.
2018.
Shoaling internal waves may reduce gravity current transport.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 2,
p.
383.
La Forgia, G.
Adduce, C.
and
Falcini, F.
2018.
Laboratory investigation on internal solitary waves interacting with a uniform slope.
Advances in Water Resources,
Vol. 120,
Issue. ,
p.
4.
Zhu, Hai
Lin, Chang
Wang, Lingling
Kao, Mingjer
Tang, Hongwu
and
Williams, J. J. R.
2018.
Numerical investigation of internal solitary waves of elevation type propagating on a uniform slope.
Physics of Fluids,
Vol. 30,
Issue. 11,
Sinnett, Gregory
Feddersen, Falk
Lucas, Andrew J.
Pawlak, Geno
and
Terrill, Eric
2018.
Observations of Nonlinear Internal Wave Run-Up to the Surfzone.
Journal of Physical Oceanography,
Vol. 48,
Issue. 3,
p.
531.
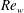 $\mathit{Re}_{w}$ are considered. Volume-integrated values of dissipation and irreversible mixing are related to the density and velocity structure of the wave throughout the breaking process. The majority of dissipation (63 %) occurs along the no-slip bottom boundary. Most of the remaining dissipation (35 %) and nearly all irreversible mixing occurs in the interior after breaking, when density overturns are present at the interface. Breaking introduces three-dimensionality to the flow field that is driven by the lateral breakdown of density overturns and the lobe–cleft instability typical of gravity currents. The resulting longitudinal rolls (streamwise vorticity) increase dissipation by roughly 8 % and decrease irreversible mixing by roughly 20 % when compared with a similar two-dimensional simulation. The bulk mixing efficiency is shown to increase for larger and smaller values of the internal Iribarren number
$\mathit{Re}_{w}$ are considered. Volume-integrated values of dissipation and irreversible mixing are related to the density and velocity structure of the wave throughout the breaking process. The majority of dissipation (63 %) occurs along the no-slip bottom boundary. Most of the remaining dissipation (35 %) and nearly all irreversible mixing occurs in the interior after breaking, when density overturns are present at the interface. Breaking introduces three-dimensionality to the flow field that is driven by the lateral breakdown of density overturns and the lobe–cleft instability typical of gravity currents. The resulting longitudinal rolls (streamwise vorticity) increase dissipation by roughly 8 % and decrease irreversible mixing by roughly 20 % when compared with a similar two-dimensional simulation. The bulk mixing efficiency is shown to increase for larger and smaller values of the internal Iribarren number 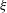 ${\it\xi}$, with a minimum for intermediate values of
${\it\xi}$, with a minimum for intermediate values of 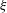 ${\it\xi}$ and a peak near
${\it\xi}$ and a peak near 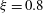 ${\it\xi}=0.8$ for plunging breakers. This trend is explained by the degree of two-dimensionality in the flow, and agrees with previous results in the literature after accounting for Reynolds number effects. Local turbulence quantities are also calculated at ‘virtual moorings’, and a location upslope of the breakpoint but downslope of the intersection of the pycnocline and the bottom is shown to provide a signal that is most representative of the volume-integrated dissipation and mixing results.
${\it\xi}=0.8$ for plunging breakers. This trend is explained by the degree of two-dimensionality in the flow, and agrees with previous results in the literature after accounting for Reynolds number effects. Local turbulence quantities are also calculated at ‘virtual moorings’, and a location upslope of the breakpoint but downslope of the intersection of the pycnocline and the bottom is shown to provide a signal that is most representative of the volume-integrated dissipation and mixing results.


