Article contents
Dynamics of laminar and transitional flows over slip surfaces: effects on the laminar–turbulent separatrix
Published online by Cambridge University Press: 04 May 2020
Abstract
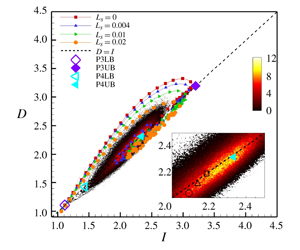
The effect of slip surfaces on the laminar–turbulent separatrix of plane Poiseuille flow is studied by direct numerical simulation. In laminar flows, the inclusion of the slip surfaces results in a drag reduction of over 10 %, which is in good agreement with previous studies and the theory of laminar slip flows. Turbulence lifetimes, the likelihood that turbulence is sustained, is investigated for transitional flows with various slip lengths. We show that slip surfaces decrease the likelihood of sustained turbulence compared to the no-slip case, and the likelihood is further decreased as slip length is increased. A more deterministic analysis of the effects of slip surfaces on a transition to turbulence is performed by using nonlinear travelling-wave solutions to the Navier–Stokes equations, also known as exact coherent solutions. Two solution families, dubbed P3 and P4, are used since their lower-branch solutions are embedded on the boundary of the basin of attraction of laminar and turbulent flows (Park & Graham, J. Fluid Mech., vol. 782, 2015, pp. 430–454). Additionally, they exhibit distinct flow structures – the P3 and P4 are denoted as core mode and critical-layer mode, respectively. Distinct effects of slip surfaces on the solutions are observed by the skin-friction evolution, linear growth rate and phase-space projection of transitional trajectories. The slip surface appears to modify the transition dynamics very little for the core mode, but quite considerably for the critical-layer mode. Most importantly, the slip surface promotes different transition dynamics – an early and bypass-like transition for the core mode and a delayed and H- or K-type-like transition for the critical-layer mode. We explain these distinct transition dynamics based on spatio-temporal and quadrant analyses. It is found that slip surfaces promote the prevalence of strong wall-toward motions (sweep-like events) near vortex cores close to the channel centre, inducing an early transition, while long sustained ejection events are present in the region of the  $\unicode[STIX]{x1D6EC}$-shaped vortex cores close to the critical layer, resulting in a delayed transition. This should motivate flow control strategies to fully exploit these distinct transition dynamics for transition to turbulence.
$\unicode[STIX]{x1D6EC}$-shaped vortex cores close to the critical layer, resulting in a delayed transition. This should motivate flow control strategies to fully exploit these distinct transition dynamics for transition to turbulence.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 12
- Cited by


