Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:41:26.317Z Has data issue: false hasContentIssue false
  • English
  • Français

Eddy diffusivities of inertial particles under gravity

Published online by Cambridge University Press:  07 February 2012

Marco Martins Afonso ,
Andrea Mazzino  and
Paolo Muratore-Ginanneschi
Marco Martins Afonso*
Affiliation:
Université de Toulouse, INP/UPS/CNRS, Institut de Mécanique des Fluides de Toulouse, groupe Particules Spray et Combustion, allée du Professeur Camille Soula, 31400 Toulouse, France Department of Mathematics and Statistics, University of Helsinki, PO Box 4, 00014 Helsinki, Finland Institut de Mathématiques et de Modélisation de Montpellier, Université Montpellier 2, case courrier 051, 34095 Montpellier CEDEX 5, France
Andrea Mazzino
Affiliation:
Department of Physics, University of Genova, and CNISM & INFN, Genova Section, via Dodecaneso 33, 16146 Genova, Italy
Paolo Muratore-Ginanneschi
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, PO Box 4, 00014 Helsinki, Finland
*
†Email address for correspondence: marcomar@fisica.unige.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The large-scale/long-time transport of inertial particles of arbitrary mass density under gravity is investigated by means of a formal multiple-scale perturbative expansion in the scale-separation parameter between the carrier flow and the particle concentration field. The resulting large-scale equation for the particle concentration is determined, and is found to be diffusive with a positive definite eddy diffusivity. The calculation of the latter tensor is reduced to the resolution of an auxiliary differential problem, consisting of a coupled set of two differential equations in a 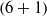-dimensional coordinate system (three space coordinates plus three velocity coordinates plus time). Although expensive, numerical methods can be exploited to obtain the eddy diffusivity, for any desirable non-perturbative limit (e.g. arbitrary Stokes and Froude numbers). The aforementioned large-scale equation is then specialized to deal with two different relevant perturbative limits: (i) vanishing of both Stokes time and sedimenting particle velocity; (ii) vanishing Stokes time and finite sedimenting particle velocity. Both asymptotics lead to a greatly simplified auxiliary differential problem, now involving only space coordinates and thus easily tackled by standard numerical techniques. Explicit, exact expressions for the eddy diffusivities have been calculated, for both asymptotics, for the class of parallel flows, both static and time-dependent. This allows us to investigate analytically the role of gravity and inertia on the diffusion process by varying relevant features of the carrier flow, such as the form of its temporal correlation function. Our results exclude a universal role played by gravity and inertia on the diffusive behaviour: regimes of both enhanced and reduced diffusion may exist, depending on the detailed structure of the carrier flow.

JFM classification

Mixing: Mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 426 - 463
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Allaire, G. 1992 Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518.CrossRefGoogle Scholar
2. Andersen, K. H., Castiglione, P., Mazzino, A. & Vulpiani, A. 2000 Simple stochastic models showing strong anomalous diffusion. Eur. Phys. J. B 18, 447–452.CrossRefGoogle Scholar
3. Avellaneda, M. & Majda, A. 1991 An integral representation and bounds on the effective diffusivity in passive advection and turbulent flows. Commun. Math. Phys. 138, 339–391.CrossRefGoogle Scholar
4. Babiano, A., Cartwright, J. H. E., Piro, O. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in Hamiltonian systems. Phys. Rev. Lett. 84, 5764–5767.CrossRefGoogle Scholar
5. Balkovsky, E., Falkovich, G. & Fouxon, A. 2001 Intermittent distribution of inertial particles in turbulent flows. Phys. Rev. Lett. 86, 2790–2793.CrossRefGoogle ScholarPubMed
6. Bec, J. 2003 Fractal clustering of inertial particles in random flows. Phys. Fluids 15, L81–L84.CrossRefGoogle Scholar
7. Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
8. Bensoussan, A., Lions, J. L. & Papanicolaou, G. 1978 Asymptotic Analysis of Periodic Structures. North-Holland.Google Scholar
9. Biferale, L., Crisanti, A., Vergassola, M. & Vulpiani, A. 1995 Eddy diffusivities in scalar transport. Phys. Fluids 7 (11), 2725–2734.CrossRefGoogle Scholar
10. Castiglione, P., Crisanti, A., Mazzino, A., Vergassola, M. & Vulpiani, A. 1998 Resonant enhanced diffusion in time-dependent flow. J. Phys. A 31, 7197–7210.CrossRefGoogle Scholar
11. Castiglione, P., Mazzino, A., Muratore-Ginanneschi, P. & Vulpiani, A. 1999 On strong anomalous diffusion. Physica D 134, 75–93.CrossRefGoogle Scholar
12. Celani, A., Martins Afonso, M. & Mazzino, A. 2006 Coarse-grained description of a passive scalar. J. Turbul. 7 (52), 1–18.CrossRefGoogle Scholar
13. Cencini, M., Bec, J., Biferale, L., Boffetta, G., Celani, A., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006a Dynamics and statistics of heavy particles in turbulent flows. J. Turbul. 7 (36), 1–36.CrossRefGoogle Scholar
14. Cencini, M., Mazzino, A., Musacchio, S. & Vulpiani, A. 2006b Large-scale effects on meso-scale modelling for scalar transport. Physica D 220, 146–156.CrossRefGoogle Scholar
15. Chandrasekhar, S. 1943 Stochastic problems in physics and astronomy. Rev. Mod. Phys. 15, 1–89.CrossRefGoogle Scholar
16. Ferrari, R. & Nikurashin, M. 2010 Suppression of eddy diffusivity across jets in the Southern Ocean. J. Phys. Oceanogr. 40, 1501–1519.CrossRefGoogle Scholar
17. Frisch, U. 1995 Turbulence. Cambridge University Press.CrossRefGoogle Scholar
18. Gardiner, C. W. 1985 Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences. Springer.CrossRefGoogle Scholar
19. Gatignol, R. 1983 The Faxén formulae for a rigid particle in an unsteady non-uniform Stokes flow. J. Méc. Théor. Appl. 1, 143–160.Google Scholar
20. Horntrop, D. J. & Majda, A. J. 1994 Subtle statistical behaviour in simple models for random advection–diffusion. J. Math. Sci. Univ. Tokyo 1, 23–70.Google Scholar
21. Kraichnan, R. H. 1987 Eddy viscosity and diffusivity: exact formulas and approximations. Complex Syst. 1, 805–820.Google Scholar
22. Lesieur, M. 1997 Turbulence in Fluids. Kluwer.CrossRefGoogle Scholar
23. Marchioli, C., Fantoni, M. & Soldati, A. 2007 Influence of added mass on anomalous high rise velocity of light particles in cellular flow field: a note on the paper by Maxey (1987). Phys. Fluids 19, 098101.CrossRefGoogle Scholar
24. Martins Afonso, M. 2008 The terminal velocity of sedimenting particles in a flowing fluid. J. Phys. A 41 (38), 385501.CrossRefGoogle Scholar
25. Martins Afonso, M. & Mazzino, A. 2011 Point-source inertial particle dispersion. Geophys. Astrophys. Fluid Dyn. 105 (6), 553–565.CrossRefGoogle Scholar
26. Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
27. Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
28. Mazzino, A. 1997 Effective correlation times in turbulent scalar transport. Phys. Rev. E 56 (5), 5500–5510.CrossRefGoogle Scholar
29. Mazzino, A. & Castiglione, P. 1999 Interference phenomena in scalar transport induced by a noise finite correlation time. Europhys. Lett. 45, 476–481.CrossRefGoogle Scholar
30. Mazzino, A., Musacchio, S. & Vulpiani, A. 2005 Multiple-scale analysis and renormalization for preasymptotic scalar transport. Phys. Rev. E 71, 011113.CrossRefGoogle ScholarPubMed
31. Mazzino, A. & Vergassola, M. 1997 Interference between turbulent and molecular diffusion. Europhys. Lett. 37 (8), 535–540.CrossRefGoogle Scholar
32. Möbius, M. E. 2006 Clustering instability in a freely falling granular jet. Phys. Rev. E 74, 051304.CrossRefGoogle Scholar
33. Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. MIT.Google Scholar
34. Nguetseng, G. 1989 A general convergence result for a functionals related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623.CrossRefGoogle Scholar
35. Obukhov, A. M. 1983 Kolmogorov flow and laboratory simulation of it. Russian Math. Surveys 38 (4), 113–126.CrossRefGoogle Scholar
36. Pavliotis, G. A. & Stuart, A. M. 2005 Periodic homogenization for inertial particles. Physica D 204, 161–187.CrossRefGoogle Scholar
37. Pavliotis, G. A. & Stuart, A. M. 2007 Multiscale methods: averaging and homogenization. In Texts in Applied Mathematics, vol. 53. Springer.Google Scholar
38. Reeks, M. W. 1988 The relationship between Brownian motion and the random motion of small particles in a turbulent flow. Phys. Fluids 31, 1314–1316.CrossRefGoogle Scholar
39. Risken, H. 1989 The Fokker–Planck Equation: Methods of Solutions and Applications. Springer.Google Scholar
40. Ruiz, J., Macías, D. & Peters, P. 2004 Turbulence increases the average settling velocity of phytoplankton cells. Proc. Natl Acad. Sci. 101, 17720–17724.CrossRefGoogle ScholarPubMed
41. Sapsis, T. & Haller, G. 2008 Instabilities in the dynamics of neutrally buoyant particles. Phys. Fluids 20, 017102.CrossRefGoogle Scholar
42. Van Kampen, N. G. 2007 Stochastic Processes in Physics and Chemistry. Elsevier.Google Scholar
43. Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008 Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237, 2084–2089.CrossRefGoogle Scholar
44. Wilkinson, M. & Mehlig, B. 2003 Path coalescence transition and its applications. Phys. Rev. E 68, 040101(R).CrossRefGoogle Scholar