Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T11:52:20.511Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of asymmetric large-scale dissipation on energy and potential enstrophy injection in two-layer quasi-geostrophic turbulence

Published online by Cambridge University Press:  02 February 2012

Eleftherios Gkioulekas
Eleftherios Gkioulekas*
Affiliation:
Department of Mathematics, University of Texas–Pan American, Edinburg, TX 78539-2999, USA
*
†Email address for correspondence: gkioulekase@utpa.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In the Nastrom–Gage spectrum of atmospheric turbulence, we observe a 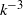energy spectrum that transitions into a 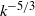spectrum, with increasing wavenumber 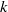. The transition occurs near a transition wavenumber 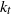, located near the Rossby deformation wavenumber 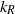. The Tung–Orlando theory interprets this spectrum as a double downscale cascade of potential enstrophy and energy, from large scales to small scales, in which the downscale potential enstrophy cascade coexists with the downscale energy cascade over the same length scale range. We show that, in a temperature-forced two-layer quasi-geostrophic model, the rates with which potential enstrophy and energy are injected place the transition wavenumbe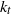r near 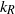. We also show that, if the potential energy dominates the kinetic energy in the forcing range, then the Ekman term suppresses the upscale cascading potential enstrophy more than it suppresses the upscale cascading energy, a behaviour contrary to what occurs in two-dimensional turbulence. As a result, the ratio 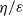of injected potential enstrophy over injected energy, in the downscale direction, decreases, thereby tending to decrease the transition wavenumber 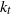further. Using a random Gaussian forcing model, we reach the same conclusion, under the modelling assumption that the asymmetric Ekman term predominantly suppresses the bottom layer forcing, thereby disregarding a possible entanglement between the Ekman term and the nonlinear interlayer interaction. Based on these results, we argue that the Tung–Orlando theory can account for the approximate coincidence between 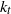and 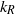. We also identify certain open questions that require further investigation via numerical simulations.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 493 - 523
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. 1969 Computation of the energy spectrum in homogeneous, two dimensional turbulence. Phys. Fluids Suppl. II 12, 233–239.CrossRefGoogle Scholar
2. Bershadskii, A., Kit, E. & Tsinober, A. 1993 Spontaneous breaking of reflexional symmetry in real quasi-two-dimensional turbulence: stochastic travelling waves and helical solitons in atmosphere and laboratory. Proc. R. Soc. Lond. A 441, 147–155.Google Scholar
3. Branover, H., Eidelman, A., Golbraikh, E. & Moiseev, S. 1999 Turbulence and Structures: Chaos, Fluctuations, and Helical Self Organization in Nature and the Laboratory. Academic Press.Google Scholar
4. Charney, J. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
5. Chkhetiani, G., Eidelman, A. & Golbraikh, E. 2006 Large- and small-scale turbulent spectra in MHD and atmospheric flows. Nonlinear Process. Geophys. 13, 613–620.Google Scholar
6. Cho, J. & Lindborg, E. 2001 Horizontal velocity structure functions in the upper troposphere and lower stratosphere. 1. Observations. J. Geophys. Res. 106 (D10), 10223–10232.CrossRefGoogle Scholar
7. Davidson, P. 2008 Cascades and fluxes in two-dimensional turbulence. Phys. Fluids 20, 025106.Google Scholar
8. Dewan, E. 1979 Stratospheric spectra resembling turbulence. Science 204, 832–835.Google Scholar
9. Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
10. Furutsu, K. 1963 On the statistical theory of electromagnetic waves in a fluctuating medium. J. Res. Natl Bur. Stand. D 67, 303–323.Google Scholar
11. Gage, K. & Nastrom, G. 1985 On the spectrum of atmospheric velocity fluctuations seen by MST/ST radar and their interpretation. Rad. Sci. 20, 1339–1347.Google Scholar
12. Gage, K. & Nastrom, G. 1986 Theoretical interpretation of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft during GASP. J. Atmos. Sci. 43, 729–740.Google Scholar
13. Gkioulekas, E. 2008 Locality and stability of the cascades of two-dimensional turbulence. Phys. Rev. E 78, 066302.CrossRefGoogle ScholarPubMed
14. Gkioulekas, E. 2010 Dissipation range and anomalous sinks in steady two-dimensional turbulence. Phys. Rev. E 82, 046304.CrossRefGoogle ScholarPubMed
15. Gkioulekas, E. & Tung, K. 2005a On the double cascades of energy and enstrophy in two dimensional turbulence. Part 1. Theoretical formulation. Discrete Continuous Dyn. Syst. B 5, 79–102.Google Scholar
16. Gkioulekas, E. & Tung, K. 2005b On the double cascades of energy and enstrophy in two dimensional turbulence. Part 2. Approach to the KLB limit and interpretation of experimental evidence. Discrete Continuous Dyn. Syst. B 5, 103–124.CrossRefGoogle Scholar
17. Gkioulekas, E. & Tung, K. 2006 Recent developments in understanding two-dimensional turbulence and the Nastrom–Gage spectrum. J. Low Temp. Phys. 145, 25–57.CrossRefGoogle Scholar
18. Gkioulekas, E. & Tung, K. 2007a Is the subdominant part of the energy spectrum due to downscale energy cascade hidden in quasi-geostrophic turbulence? Discrete Continuous Dyn. Syst. B 7, 293–314.CrossRefGoogle Scholar
19. Gkioulekas, E. & Tung, K. 2007b A new proof on net upscale energy cascade in 2D and QG turbulence. J. Fluid. Mech. 576, 173–189.CrossRefGoogle Scholar
20. Hamilton, K., Takahashi, Y. & Ohfuchi, W. 2008 The mesoscale spectrum of atmospheric motions investigated in a very fine resolution global general circulation model. J. Geophys. Res. 113, D18110.Google Scholar
21. Holm, D., Livescu, D., Jeffery, C., Kurien, S., Taylor, M. & Wingate, B. 2005 The LANS- model for computing turbulence: origins, results and open problems. Los Alamos Science 29, 152–171.Google Scholar
22. Kaneda, Y. & Ishihira, T. 2001 Nonuniversal energy spectrum in stationary two-dimensional homogeneous turbulence. Phys. Fluids 13, 1431–1439.CrossRefGoogle Scholar
23. Koshyk, J. & Hamilton, K. 2001 The horizontal kinetic energy spectrum and spectral budget simulated by a high-resolution troposphere–stratosphere mesosphere GCM. J. Atmos. Sci. 58, 329–348.2.0.CO;2>CrossRefGoogle Scholar
24. Koshyk, J., Hamilton, K. & Mahlman, J. 1999 Simulation of the mesoscale spectral regime in the GFDL SKYHI general circulation model. Geophys. Res. Lett. 26, 843–846.CrossRefGoogle Scholar
25. Kraichnan, R. 1967 Inertial ranges in two dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
26. Leith, C. 1968 Diffusion approximation for two dimensional turbulence. Phys. Fluids 11, 671–673.Google Scholar
27. Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid. Mech. 550, 207–242.Google Scholar
28. Lindborg, E. 2007 Horizontal wavenumber spectra of vertical vorticity and horizontal divergence in the upper troposphere and lower stratosphere. J. Atmos. Sci. 64, 1017–1025.Google Scholar
29. Lindborg, E. & Alvelius, K. 2000 The kinetic energy spectrum of two dimensional enstrophy turbulence cascade. Phys. Fluids 12, 945–947.Google Scholar
30. McComb, W. 1990 The Physics of Fluid Turbulence. Clarendon.CrossRefGoogle Scholar
31. Moiseev, S. & Chkhetiani, O. 1996 Helical scaling in turbulence. J. Expl Theor. Phys. 83, 192–198.Google Scholar
32. Nastrom, G. & Gage, K. 1984 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.Google Scholar
33. Novikov, E. 1965 Functionals and the random force method in turbulence. Sov. Phys. JETP 20, 1290.Google Scholar
34. Pasquero, C. & Falkovich, G. 2002 Stationary spectrum of vorticity cascade in two dimensional turbulence. Phys. Rev. E 65, 056305.CrossRefGoogle ScholarPubMed
35. Salmon, R. 1978 Two-layer quasi-geostrophic turbulence in a simple special case. Geophys. Astrophys. Fluid Dyn. 10, 25–52.Google Scholar
36. Salmon, R. 1980 Baroclinic instability and geostrophic turbulence. Geophys. Astrophys. Fluid Dyn. 15, 167–211.CrossRefGoogle Scholar
37. Skamarock, W. 2004 Evaluating mesoscale NWP models using kinetic energy spectra. Mon. Weath. Rev. 132, 3019–3032.Google Scholar
38. Smith, K. 2004 Comment on: the and energy spectrum of the atmospheric turbulence: quasi-geostrophic two level model simulation. J. Atmos. Sci. 61, 937–942.Google Scholar
39. Takahashi, Y., Hamilton, K. & Ohfuchi, W. 2006 Explicit global simulation of the mesoscale spectrum of atmospheric motions. Geophys. Res. Lett. 33, L12812.CrossRefGoogle Scholar
40. Terasaki, K., Tanaka, H. & Zagar, N. 2011 Energy spectra of Rossby and gravity waves. SOLA 7, 45–48.CrossRefGoogle Scholar
41. Tulloch, R. & Smith, K. 2006 A theory for the atmospheric energy spectrum: depth-limited temperature anomalies at the tropopause. Proc. Natl Acad. Sci. USA 103, 14690–14694.Google Scholar
42. Tulloch, R. & Smith, K. S. 2009 Quasigeostrophic turbulence with explicit surface dynamics: application to the atmospheric energy spectrum. J. Atmos. Sci. 66, 450–467.CrossRefGoogle Scholar
43. Tung, K. 2004 Reply to comments by K. Shafer Smith. J. Atmos. Sci. 61, 943–948.2.0.CO;2>CrossRefGoogle Scholar
44. Tung, K. & Orlando, W. 2003a The and energy spectrum of the atmospheric turbulence: quasi-geostrophic two level model simulation. J. Atmos. Sci. 60, 824–835.Google Scholar
45. Tung, K. & Orlando, W. 2003b On the differences between 2D and QG turbulence. Discrete Continuous Dyn. Syst. B 3, 145–162.Google Scholar
46. Tung, K. & Welch, W. 2001 Remarks on note on geostrophic turbulence. J. Atmos. Sci. 58, 2009–2012.2.0.CO;2>CrossRefGoogle Scholar
47. Vallgren, A. & Lindborg, E. 2010 Charney isotropy and equipartition in quasi-geostrophic turbulence. J. Fluid. Mech. 656, 448–457.CrossRefGoogle Scholar
48. VanZadt, T. 1982 A universal spectrum of buoyancy waves in the atmosphere. Geophys. Res. Lett. 9, 575–578.CrossRefGoogle Scholar