Published online by Cambridge University Press: 15 October 2019
The flow over a square cylinder controlled by a slot synthetic jet positioned at the front surface is investigated experimentally at different excitation frequencies. The Reynolds number based on the free-stream velocity and the side length of the square cylinder is 1000. The flow visualization was conducted using the laser-induced fluorescence technique. The velocity fields upstream and downstream of the square cylinder were measured synchronously with the two-dimensional time-resolved particle image velocimetry technique. Both the evolution of vortex structures and the characteristic frequencies of upstream and downstream flow fields are presented. The flow dynamics vary significantly with the excitation frequency at a fixed stroke length. During one excitation cycle, the synthetic jet vortex pair deflects to one side and later swings to the other side at a quite small excitation frequency of  $f_{e}/f_{0}=0.6$, while it only deflects toward one side and does not turn to the other side at
$f_{e}/f_{0}=0.6$, while it only deflects toward one side and does not turn to the other side at  $f_{e}/f_{0}=1.0$. Compared with the natural case, the wake characteristics for the above two cases are not changed much by the synthetic jet adopted. At a moderate excitation frequency of
$f_{e}/f_{0}=1.0$. Compared with the natural case, the wake characteristics for the above two cases are not changed much by the synthetic jet adopted. At a moderate excitation frequency of 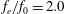 $f_{e}/f_{0}=2.0$, the synthetic jet deflects upwards and downwards alternatively. The upstream flow field has a dominant frequency identical to half of the excitation frequency. Under the perturbations of the synthetic jet, two wake vortex pairs are formed per shedding cycle with a shedding frequency equal to that of the square cylinder without control. At a higher excitation frequency of
$f_{e}/f_{0}=2.0$, the synthetic jet deflects upwards and downwards alternatively. The upstream flow field has a dominant frequency identical to half of the excitation frequency. Under the perturbations of the synthetic jet, two wake vortex pairs are formed per shedding cycle with a shedding frequency equal to that of the square cylinder without control. At a higher excitation frequency of 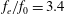 $f_{e}/f_{0}=3.4$, the synthetic jet keeps deflecting to one side, and the upstream flow field is governed by the excitation frequency. The flow separation on the deflected side is suppressed effectively, and no periodic vortex shedding can be observed in the wake. Statistically, the velocity profiles also change with control. The recirculation bubble length in the wake is shortened, and the time-averaged velocity fluctuation is weakened remarkably. The control effects of the synthetic jet and the continuous jet are compared in this paper when placed at the front surface of a square cylinder.
$f_{e}/f_{0}=3.4$, the synthetic jet keeps deflecting to one side, and the upstream flow field is governed by the excitation frequency. The flow separation on the deflected side is suppressed effectively, and no periodic vortex shedding can be observed in the wake. Statistically, the velocity profiles also change with control. The recirculation bubble length in the wake is shortened, and the time-averaged velocity fluctuation is weakened remarkably. The control effects of the synthetic jet and the continuous jet are compared in this paper when placed at the front surface of a square cylinder.