Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T18:06:36.773Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of finite-conductivity Hartmann walls on the linear stability of Hunt’s flow

Published online by Cambridge University Press:  08 June 2017

Thomas Arlt Open the ORCID record for Thomas Arlt [Opens in a new window] ,
Jānis Priede Open the ORCID record for Jānis Priede [Opens in a new window]  and
Leo Bühler
Thomas Arlt*
Affiliation:
Institut für Kern- und Energietechnik, Karlsruhe Institute of Technology, Postfach 3640, 76021 Karlsruhe, Germany
Jānis Priede
Affiliation:
Applied Mathematics Research Centre, Coventry University, Coventry CV1 5FB, UK
Leo Bühler
Affiliation:
Institut für Kern- und Energietechnik, Karlsruhe Institute of Technology, Postfach 3640, 76021 Karlsruhe, Germany
*
†Email address for correspondence: Thomas.Arlt@kit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse numerically the linear stability of fully developed liquid metal flow in a square duct with insulating side walls and thin, electrically conducting horizontal walls. The wall conductance ratio $c$ is in the range of 0.01 to 1 and the duct is subject to a vertical magnetic field with Hartmann numbers up to 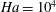$\mathit{Ha}=10^{4}$. In a sufficiently strong magnetic field, the flow consists of two jets at the side walls and a near-stagnant core with relative velocity 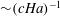${\sim}(c\mathit{Ha})^{-1}$. We find that for 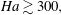$\mathit{Ha}\gtrsim 300,$ the effect of wall conductivity on the stability of the flow is mainly determined by the effective Hartmann wall conductance ratio 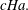$c\mathit{Ha}.$ For 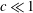$c\ll 1$, the increase of the magnetic field or that of the wall conductivity has a destabilizing effect on the flow. Maximal destabilization of the flow occurs at 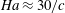$\mathit{Ha}\approx 30/c$. In a stronger magnetic field with 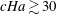$c\mathit{Ha}\gtrsim 30$, the destabilizing effect vanishes and the asymptotic results of Priede et al. (J. Fluid Mech., vol. 649, 2010, pp. 115–134) for ideal Hunt’s flow with perfectly conducting Hartmann walls are recovered.

JFM classification

MHD and Electrohydrodynamics: High-Hartmann-number flows Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 880 - 891
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
Bayly, B. J., Orszag, S. A. & Herbert, T. 1988 Instability mechanisms in shear-flow transition. Annu. Rev. Fluid Mech. 20 (1), 359–391.CrossRefGoogle Scholar
Bühler, L. 2007 Liquid metal magnetohydrodynamics for fusion blankets. In Magnetohydrodynamics: Historical Evolution and Trends, pp. 171–194. Springer.Google Scholar
Chang, C. C. & Lundgren, T. S. 1961 Duct flow in magnetohydrodynamics. Z. Angew. Math. Phys. 12 (2), 100–114.Google Scholar
Hunt, J. C. R. 1965 Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 21 (04), 577–590.CrossRefGoogle Scholar
Jackson, J. D. 1998 Classical Electrodynamics. Wiley.Google Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2010 Linear stability of Hunt’s flow. J. Fluid Mech. 649, 115–134.Google Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2012 Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct. J. Fluid Mech. 708, 111–127.Google Scholar
Priede, J., Arlt, T. & Bühler, L. 2015 Linear stability of magnetohydrodynamic flow in a square duct with thin conducting walls. J. Fluid Mech. 788, 129–146.CrossRefGoogle Scholar
Roberts, P. H. 1967 An Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Schmid, P. J. & Henningson, D. S. 2012 Stability and Transition in Shear Flows. Springer.Google Scholar
Shercliff, J. A. 1956 The flow of conducting fluids in circular pipes under transverse magnetic fields. J. Fluid Mech. 1 (06), 644–666.CrossRefGoogle Scholar
Tatsumi, T. & Yoshimura, T. 1990 Stability of the laminar flow in a rectangular duct. J. Fluid Mech. 212, 437–449.CrossRefGoogle Scholar
Uflyand, Y. S. 1961 Flow stability of a conducting fluid in a rectangular channel in a transverse magnetic field. Sov. Phys. 5 (10), 1191–1193.Google Scholar
Uhlmann, M. & Nagata, M. 2006 Linear stability of flow in an internally heated rectangular duct. J. Fluid Mech. 551, 387–404.Google Scholar
Walker, J. S. 1981 Magneto-hydrodynamic flows in rectangular ducts with thin conducting walls. J. Méc. 20 (1), 79–112.Google Scholar
Zikanov, O., Krasnov, D., Boeck, T., Thess, A. & Rossi, M. 2014 Laminar-turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 66 (3), 030802.Google Scholar