Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T22:36:06.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of hinged leaflets on vortex pair generation

Published online by Cambridge University Press:  02 August 2013

Prashant Das ,
R. N. Govardhan  and
J. H. Arakeri
Prashant Das
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
R. N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
J. H. Arakeri
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
*
†Email address for correspondence: raghu@mecheng.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally study the effect of having hinged leaflets at the jet exit on the formation of a two-dimensional counter-rotating vortex pair. A piston–cylinder mechanism is used to generate a starting jet from a high-aspect-ratio channel into a quiescent medium. For a rigid exit, with no leaflets at the channel exit, the measurements at a central plane show that the trailing jet in the present case is never detached from the vortex pair, and keeps feeding into the latter, unlike in the axisymmetric case. Passive flexibility is introduced in the form of rigid leaflets or flaps that are hinged at the exit of the channel, with the flaps initially parallel to the channel walls. The experimental arrangement closely approximates the limiting case of a free-to-rotate rigid flap with negligible structural stiffness, damping and flap inertia, as these limiting structural properties permit the largest flap openings. Using this arrangement, we start the flow and measure the flap kinematics and the vorticity fields for different flap lengths and piston velocity programs. The typical motion of the flaps involves a rapid opening and a subsequent more gradual return to its initial position, both of which occur when the piston is still moving. The initial opening of the flaps can be attributed to an excess pressure that develops in the channel when the flow starts, due to the acceleration that has to be imparted to the fluid slug between the flaps. In the case with flaps, two additional pairs of vortices are formed because of the motion of the flaps, leading to the ejection of a total of up to three vortex pairs from the hinged exit. The flaps’ length (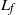${L}_{f} $) is found to significantly affect flap motions when plotted using the conventional time scale 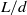$L/ d$, where 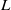$L$ is the piston stroke and 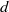$d$ is the channel width. However, with a newly defined time scale based on the flap length (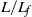$L/ {L}_{f} $), we find a good collapse of all the measured flap motions irrespective of flap length and piston velocity for an impulsively started piston motion. The maximum opening angle in all these impulsive velocity program cases, irrespective of the flap length, is found to be close to 15°. Even though the flap kinematics collapses well with 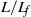$L/ {L}_{f} $, there are differences in the distribution of the ejected vorticity even for the same 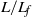$L/ {L}_{f} $. Such a redistribution of vorticity can lead to important changes in the overall properties of the flow, and it gives us a better understanding of the importance of exit flexibility in such flows.

JFM classification

Wakes/Jets: Jets Biological Fluid Dynamics: Propulsion Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 626 - 658
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. 2006 Formation of vortex dipoles. Phys. Fluids 18 (3) 037103.Google Scholar
Anderson, E. J. & Demont, M. E. 2000 The mechanics of locomotion in the squid Loligo pealei: locomotory function and unsteady hydrodynamics of the jet and intramantle pressure. J. Expl Biol. 203, 2851–2863.CrossRefGoogle ScholarPubMed
Arakeri, J. H., Das, D., Krothapalli, A. & Lourenco, L. 2004 Vortex ring formation at the open end of a shock tube: a particle image velocimetry study. Phys. Fluids 16 (4), 1008–1019.Google Scholar
Auerbach, D. 1987 Experiments on the trajectory and the circulation of the starting vortex. J. Fluid Mech. 183, 185–198.Google Scholar
Brennen, C. E. 1982 A review of added mass and fluid inertial forces. Tech. Rep., Department of the Navy, Port Hueneme, CA, USA.Google Scholar
Cheng, J. Y. & Demont, M. E. 1996 Hydrodynamics of scallop locomotion: unsteady fluid forces on clapping shells. J. Fluid Mech. 317, 73–90.Google Scholar
Dabiri, J. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.Google Scholar
Dabiri, J. O., Colin, S. P. & Costello, J. H. 2006 Fast-swimming hydromedusae exploit velar kinematics to form an optimal vortex wake. J. Expl Biol. 209 (11), 2025–2033.Google Scholar
Dabiri, J. & Gharib, M. 2005a The role of optimal vortex formation in biological fluid transport. Proc. R. Soc. B 272, 1557–1560.CrossRefGoogle ScholarPubMed
Dabiri, J. O. & Gharib, M. 2005b Starting flow through nozzles with temporally variable exit diameter. J. Fluid Mech. 538, 111–136.Google Scholar
Dabiri, J. O., Gharib, M., Colin, S. P. & Costello, J. H. 2005 Vortex motion in the ocean: in situ visualization of jellyfish swimming and feeding flows. Phys. Fluids 17 (9)091108.Google Scholar
Dasi, L. P., Ge, L., Simon, H. A., Sotiropoulos, F. & Yoganathan, A. P. 2007 Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys. Fluids 19 (6)067105.Google Scholar
Didden, N. 1979 Formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.CrossRefGoogle Scholar
Domenichini, F., Pedrizzetti, G. & Baccani, B. 2005 Three-dimensional filling flow into a model left ventricle. J. Fluid Mech. 539, 179–198.Google Scholar
Gharib, M., Rambod, E., Kheradvar, A., Sahn, D. J. & Dabiri, J. O. 2006 Optimal vortex formation as an index of cardiac health. Proc. Natl Acad. Sci. USA 103, 6305–6308.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31, 3532–3542.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Kim, D. W. Y., Walker, P. G., Pedersen, E. M., Poulsen, J. K., Oyre, S., Houlind, K. & Yoganathan, A. P. 1995 Left ventricular blood flow patterns in normal subjects: a quantitative analysis by three-dimensional magnetic resonance velocity mapping. J. Am. College of Cardiology 26, 224–238.CrossRefGoogle ScholarPubMed
Krueger, P. 2005 An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 545, 427–443.Google Scholar
Krueger, P. S. & Gharib, M. 2003 The significance of vortex ring formation to the impulse and thrust of a starting jet. Phys. Fluids 15, 1271–1281.CrossRefGoogle Scholar
Lee, C. S. F & Talbot, L. 1979 A fluid-mechanical study of the closure of heart valves. J. Fluid Mech. 91, 41–63.CrossRefGoogle Scholar
Lim, T. T. & Nickels, T. B. 1995 Vortex rings. In Fluid Vortices, pp. 95–153. Kluwer.Google Scholar
Linden, P. F. & Turner, J. S. 2004 ‘Optimal’ vortex rings and aquatic propulsion mechanisms. Proc. R. Soc. Lond. B 271 (1539), 647–653.Google Scholar
Lisoski, D. L. A. 1993 Nominally two-dimensional flow about a normal flat plate. PhD thesis, California Institute of Technology.Google Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51, 15–32.CrossRefGoogle Scholar
Maxworthy, T. 1974 Turbulent vortex rings. J. Fluid Mech. 64, 227–239.Google Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81, 465–495.Google Scholar
Mohseni, K., Ran, H. & Colonius, T. 2001 Numerical experiments on vortex ring formation. J. Fluid Mech. 430, 267–282.Google Scholar
Pedrizzetti, G. 2010 Vortex formation out of two-dimensional orifices. J. Fluid Mech. 655, 198–216.Google Scholar
Pedrizzetti, G. & Domenichini, F. 2006 Flow-driven opening of a valvular leaflet. J. Fluid Mech. 569, 321–330.Google Scholar
Pedrizzetti, G. & Domenichini, F. 2007 Asymmetric opening of a simple bileaflet valve. Phys. Rev. Lett. 98, 214503.CrossRefGoogle ScholarPubMed
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.Google Scholar
Romano, G. P., Querzoli, G. & Falchi, M. 2009 Investigation of vortex dynamics downstream of moving leaflets using robust image velocimetry. Exp. Fluids 47, 827–838.Google Scholar
Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation number of laminar vortex rings. J. Fluid Mech. 376, 297–318.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12 (3), 618–621.CrossRefGoogle Scholar
Shusser, M., Rosenfeld, M., Dabiri, J. O. & Gharib, M. 2006 Effect of time-dependent piston velocity program on vortex ring formation in a piston/cylinder arrangement. Phys. Fluids 18 (3) 033601.Google Scholar
Yoganathan, A. P., He, Z. & Jones, S. C. 2004 Fluid mechanics of heart valves. Annu. Rev. Biomed. Engng 6, 331–362.Google Scholar