Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-30T21:31:45.875Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of imposed rotary oscillation on the flow-induced vibration of a sphere

Published online by Cambridge University Press:  19 September 2018

A. Sareen Open the ORCID record for A. Sareen [Opens in a new window] ,
J. Zhao ,
J. Sheridan ,
K. Hourigan  and
M. C. Thompson
A. Sareen*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
J. Zhao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
J. Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: anchal.sareen@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This experimental study investigates the effect of imposed rotary oscillation on the flow-induced vibration of a sphere that is elastically mounted in the cross-flow direction, employing simultaneous displacement, force and vorticity measurements. The response is studied over a wide range of forcing parameters, including the frequency ratio 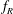$f_{R}$ and velocity ratio $\unicode[STIX]{x1D6FC}_{R}$ of the oscillatory forcing, which vary between 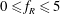$0\leqslant f_{R}\leqslant 5$ and 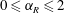$0\leqslant \unicode[STIX]{x1D6FC}_{R}\leqslant 2$. The effect of another important flow parameter, the reduced velocity, 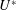$U^{\ast }$, is also investigated by varying it in small increments between 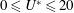$0\leqslant U^{\ast }\leqslant 20$, corresponding to the Reynolds number range of 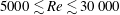$5000\lesssim Re\lesssim 30\,000$. It has been found that when the forcing frequency of the imposed rotary oscillations, 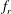$f_{r}$, is close to the natural frequency of the system, 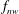$f_{nw}$, (so that 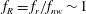$f_{R}=f_{r}/f_{nw}\sim 1$), the sphere vibrations lock on to 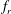$f_{r}$ instead of 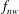$f_{nw}$. This inhibits the normal resonance or lock-in leading to a highly reduced vibration response amplitude. This phenomenon has been termed ‘rotary lock-on’, and occurs for only a narrow range of 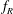$f_{R}$ in the vicinity of 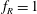$f_{R}=1$. When rotary lock-on occurs, the phase difference between the total transverse force coefficient and the sphere displacement, 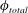$\unicode[STIX]{x1D719}_{total}$, jumps from 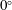$0^{\circ }$ (in phase) to 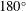$180^{\circ }$ (out of phase). A corresponding dip in the total transverse force coefficient 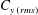$C_{y\,(rms)}$ is also observed. Outside the lock-on boundaries, a highly modulated amplitude response is observed. Higher velocity ratios (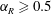$\unicode[STIX]{x1D6FC}_{R}\geqslant 0.5$) are more effective in reducing the vibration response of a sphere to much lower values. The mode I sphere vortex-induced vibration (VIV) response is found to resist suppression, requiring very high velocity ratios (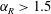$\unicode[STIX]{x1D6FC}_{R}>1.5$) to significantly suppress vibrations for the entire range of 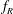$f_{R}$ tested. On the other hand, mode II and mode III are suppressed for 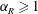$\unicode[STIX]{x1D6FC}_{R}\geqslant 1$. The width of the lock-on region increases with an increase in 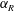$\unicode[STIX]{x1D6FC}_{R}$. Interestingly, a reduction of VIV is also observed in non-lock-on regions for high 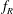$f_{R}$ and 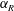$\unicode[STIX]{x1D6FC}_{R}$ values. For a fixed 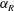$\unicode[STIX]{x1D6FC}_{R}$, when 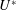$U^{\ast }$ is progressively increased, the response of the sphere is very rich, exhibiting characteristically different vibration responses for different 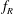$f_{R}$ values. The phase difference between the imposed rotary oscillation and the sphere displacement 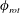$\unicode[STIX]{x1D719}_{rot}$ is found to be crucial in determining the response. For selected 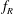$f_{R}$ values, the vibration amplitude increases monotonically with an increase in flow velocity, reaching magnitudes much higher than the peak VIV response for a non-rotating sphere. For these cases, the vibrations are always locked to the forcing frequency, and there is a linear decrease in 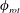$\unicode[STIX]{x1D719}_{rot}$. Such vibrations have been termed ‘rotary-induced vibrations’. The wake measurements in the cross-plane 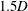$1.5D$ downstream of the sphere position reveal that the sphere wake consists of vortex loops, similar to the wake of a sphere without any imposed rotation; however, there is a change in the timing of vortex formation. On the other hand, for high 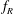$f_{R}$ values, there is a reduction in the streamwise vorticity, presumably leading to a decreased total transverse force acting on the sphere and resulting in a reduced response.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 703 - 735
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.Google Scholar
Baek, S. J. & Sung, H. J. 2000 Quasi-periodicity in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 408, 275–300.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.Google Scholar
Behara, S., Borazjani, I. & Sotiropoulos, F. 2011 Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at Re = 300: hysteresis and vortex shedding modes. J. Fluid Mech. 686, 426–450.Google Scholar
Behara, S. & Sotiropoulos, F. 2016 Vortex-induced vibrations of an elastically mounted sphere: the effects of Reynolds number and reduced velocity. J. Fluids Struct. 66, 54–68.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration, 2nd edn. Krieger Publishing Company.Google Scholar
Bokaian, A. & Geoola, F. 1984 Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.Google Scholar
Brika, D. & Laneville, A. 1999 The flow interaction between a stationary cylinder and a downstream flexible cylinder. J. Fluids Struct. 13 (5), 579–606.Google Scholar
Cheng, M., Chew, Y. T. & Luo, S. C. 2001 Numerical investigation of a rotationally oscillating cylinder in mean flow. J. Fluids Struct. 15 (7), 981–1007.Google Scholar
Choi, H., Jeon, W. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.Google Scholar
Choi, S., Choi, H. & Kang, S. 2002 Characteristics of flow over a rotationally oscillating cylinder at low Reynolds number. Phys. Fluids 14 (8), 2767–2777.Google Scholar
Chou, M. H. 1997 Synchronization of vortex shedding from a cylinder under rotary oscillation. Comput. Fluids 26 (8), 755–774.Google Scholar
Dong, S., Triantafyllou, G. S. & Karniadakis, G. E. 2008 Elimination of vortex streets in bluff-body flows. Phys. Rev. Lett. 100 (20), 204501.Google Scholar
Du, L. & Sun, X. 2015 Suppression of vortex-induced vibration using the rotary oscillation of a cylinder. Phys. Fluids 27 (2), 023603.Google Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.Google Scholar
Govardhan, R. & Williamson, C. H. K. 1997 Vortex-induced motions of a tethered sphere. J. Wind Engng Ind. Aerodyn. 69, 375–385.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.Google Scholar
van Hout, R., Krakovich, A. & Gottlieb, O. 2010 Time resolved measurements of vortex-induced vibrations of a tethered sphere in uniform flow. Phys. Fluids 22 (8), 087101.Google Scholar
Jauvtis, N., Govardhan, R. & Williamson, C. H. K. 2001 Multiple modes of vortex-induced vibration of a sphere. J. Fluids Struct. 15 (3–4), 555–563.Google Scholar
Krakovich, A., Eshbal, L. & van Hout, R. 2013 Vortex dynamics and associated fluid forcing in the near wake of a light and heavy tethered sphere in uniform flow. Exp. Fluids 54 (11), 1615.Google Scholar
Kumar, S., Lopez, C., Probst, O., Francisco, G., Askari, D. & Yang, Y. 2013 Flow past a rotationally oscillating cylinder. J. Fluid Mech. 735, 307–346.Google Scholar
Lee, H., Hourigan, K. & Thompson, M. C. 2013 Vortex-induced vibration of a neutrally buoyant tethered sphere. J. Fluid Mech. 719, 97–128.Google Scholar
Lee, S. & Lee, J. 2006 Flow structure of wake behind a rotationally oscillating circular cylinder. J. Fluids Struct. 22 (8), 1097–1112.Google Scholar
Lu, X. Y. & Sato, J. 1996 A numerical study of flow past a rotationally oscillating circular cylinder. J. Fluids Struct. 10 (8), 829–849.Google Scholar
Mahfouz, F. M. & Badr, H. M. 2000 Flow structure in the wake of a rotationally oscillating cylinder. Trans. ASME J. Fluids Engng 122 (2), 290–301.Google Scholar
Mittal, S. 2001 Control of flow past bluff bodies using rotating control cylinders. J. Fluids Struct. 15 (2), 291–326.Google Scholar
Naudascher, E. & Rockwell, D. 2012 Flow-Induced Vibrations: An Engineering Guide. Courier Corporation.Google Scholar
Païdoussis, M. P., Price, S. & De Langre, E. 2010 Fluid-Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Pregnalato, C. J.2003 Flow-induced vibrations of a tethered sphere. PhD thesis, Monash University.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME J. Fluids Engng 112, 386–392.Google Scholar
Sareen, A., Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018a Vortex-induced vibration of a rotating sphere. J. Fluid Mech. 837, 258–292.Google Scholar
Sareen, A., Zhao, J., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018b Vortex-induced vibrations of a sphere close to a free surface. J. Fluid Mech. 846, 1023–1058.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Shiels, D. & Leonard, A. 2001 Investigation of a drag reduction on a circular cylinder in rotary oscillation. J. Fluid Mech. 431, 297–322.Google Scholar
Taneda, S. 1978 Visual observations of the flow past a circular cylinder performing a rotatory oscillation. J. Phys. Soc. Japan 45 (3), 1038–1043.Google Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.Google Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1991 Rotary oscillation control of a cylinder wake. J. Fluid Mech. 224, 77–90.Google Scholar
Venning, J. A.2016 Vortex structures in the wakes of two- and three-dimensional bodies. PhD thesis, Monash University.Google Scholar
Williamson, C. H. K. & Govardhan, R. 1997 Dynamics and forcing of a tethered sphere in a fluid flow. J. Fluids Struct. 11 (3), 293–305.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36 (1), 413–455.Google Scholar
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. & Sheridan, J. 2018 Experimental investigation of flow-induced vibrations of a sinusoidally rotating circular cylinder. J. Fluid Mech. 848, 430–466.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014a Chaotic vortex induced vibrations. Phys. Fluids 26 (12), 121702.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014b Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 Experimental investigation of in-line flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 847, 664–699.Google Scholar