Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T01:34:30.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of microstructural anisotropy on the fluid–particle drag force and the stability of the uniformly fluidized state

Published online by Cambridge University Press:  26 October 2012

William Holloway ,
Jin Sun  and
Sankaran Sundaresan
William Holloway*
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
Jin Sun
Affiliation:
School of Engineering, University of Edinburgh, Edinburgh EH9 3JL, Scotland, UK
Sankaran Sundaresan
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: whollowa@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Lattice-Boltzmann simulations of fluid flow through sheared assemblies of monodisperse spherical particles have been performed. The friction coefficient tensor extracted from these simulations is found to become progressively more anisotropic with increasing Péclet number, 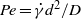$Pe= \dot {\gamma } {d}^{2} / D$, where 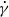$\dot {\gamma } $ is the shear rate, 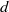$d$ is the particle diameter, and 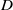$D$ is the particle self-diffusivity. A model is presented for the anisotropic friction coefficient, and the model constants are related to changes in the particle microstructure. Linear stability analysis of the two-fluid model equations including the anisotropic drag force model developed in the present study reveals that the uniformly fluidized state of low Reynolds number suspensions is most unstable to mixed mode disturbances that take the form of vertically travelling waves having both vertical and transverse structures. As the Stokes number increases, the transverse-to-vertical wavenumber ratio decreases towards zero; i.e. the transverse structure becomes progressively less prominent. Fully nonlinear two-fluid model simulations of moderate to high Stokes number suspensions reveal that the anisotropic drag model leads to coarser gas–particle flow structures than the isotropic drag model.

JFM classification

Complex Fluids: Complex Fluids Instability: Instability Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 27 - 49
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, M., Climent, E. & Simonin, O. 2009 Shear-induced self-diffusion of inertial particles in a viscous fluid. Phys. Rev. E 79, 036313.CrossRefGoogle Scholar
Agrawal, K., Loezos, P. N., Syamlal, M. & Sundaresan, S. 2001 The role of meso-scale structures in rapid gas–solid flows. J. Fluid Mech. 445, 151–185.Google Scholar
Anderson, K., Sundaresan, S. & Jackson, R. 1995 Instabilities and the formation of bubbles in fluidized beds. J. Fluid Mech. 303, 327–366.Google Scholar
Anderson, T. B. & Jackson, R. 1969 A fluid mechanical description of fluidized beds. Comparison of theory and experiment. Ind. Engng Chem. Fundam. 8, 137–144.Google Scholar
Batchelor, G. K. 1988 A new theory of the instability of a uniformly fluidized bed. J. Fluid Mech. 193, 75–110.Google Scholar
Beetstra, R., Van Der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 53, 489–501.CrossRefGoogle Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 101–139.CrossRefGoogle Scholar
Brady, J. F. & Vicic, J. F. 1995 Normal stresses in colloidal dispersions. J. Rheol. 39, 545–566.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice-Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2002 Deterministic and stochastic behaviour of non-brownian spheres in sheared suspensions. J. Fluid Mech. 460, 307–335.Google Scholar
Duru, P. & Guazzelli, E. 2002 Experimental investigation on the secondary instability of liquid-fluidized beds and the formation of bubbles. J. Fluid Mech. 470, 359–382.Google Scholar
Fan, L. S. & Zhu, C. 1998 Principles of Gas–Solids Flows. Cambridge University Press.Google Scholar
Garzó, V. & Dufty, J. W. 1999 Dense fluid transport for inelastic hard spheres. Phys. Rev. E 59, 5895–5713.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic.Google Scholar
Glasser, B. J., Kevrekidis, I. G. & Sundaresan, S. 1996 One- and two-dimensional travelling wave solutions in gas-fluidized beds. J. Fluid Mech. 334, 183–221.Google Scholar
Glasser, B. J., Kevrekidis, I. G. & Sundaresan, S. 1997 Fully developed travelling wave solutions and bubble formation in fluidized beds. J. Fluid Mech. 334, 157–188.Google Scholar
Glasser, B. J., Sundaresan, S. & Kevrekidis, I. G. 1998 From bubbles to clusters in fluidized beds. Phys. Rev. Lett. 81, 1849–1852.Google Scholar
Goldhirsch, I. & Zanetti, G. 1993 Clustering instability in dissipative gases. Phys. Rev. Lett. 70, 1619–1622.Google Scholar
Guazzelli, E. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–110.Google Scholar
Ham, J. M., Thomas, S., Guazzelli, E., Homsy, G. M. & Anselmet, M.-C. 1990 An experimental study of the stability of liquid-fluidized beds. Intl J. Multiphase Flow 16, 171–185.Google Scholar
van der Hoef, M. A., Beetstra, R. & Kuipers, J. A. M. 2005 Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: results for permeability and drag force. J. Fluid Mech. 528, 233–254.Google Scholar
Jackson, R. 2000 The Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Koch, D. L. 1990 Kinetic theory for a monodisperse gas–solid suspension. Phys. Fluids A 2, 1711–1723.Google Scholar
Koch, D. L. & Sangani, A. S. 1999 Particle pressure and marginal stability limits for a homogeneous monodisperse gas-fluidized bed: kinetic theory and numerical simulations. J. Fluid Mech. 400, 229–263.CrossRefGoogle Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. General theory. J. Fluid Mech. 271, 285–309.Google Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.Google Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice-Boltzmann simulations of particle-fluid suspensions. J. Stat. Phys. 104, 1191–1251.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slight inelastic particles in a general flow field. J. Fluid Mech. 140, 223–256.Google Scholar
Ma, D. & Ahmadi, G. 1988 A kinetic model for rapid granular flows of nearly elastic particles including interstitial fluid effects. Powder Technol. 56, 191.Google Scholar
Mucha, P. J., Tee, S. Y., Weitz, D. A., Shraiman, B. I. & Brenner, M. P. 2004 A model for velocity fluctuations in sedimentation. J. Fluid Mech. 501, 71–104.Google Scholar
Nicolas, M., Chomaz, J. M., Denis, V & Guazzelli, E. 1996 Experimental investigation on the nature of the first wavy instability in liquid fluidized beds. Phys. Fluids 8, 1987–1989.Google Scholar
Phung, T. N., Brady, J. F. & Bossis, G. 1996 Stokesian dynamics simulation of Brownian suspensions. J. Fluid Mech. 313, 181–207.Google Scholar
Plimpton, S. 1995 Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19.Google Scholar
Renard, Ph. & Marsily, G. D. 1997 Calculating equivalent permeability: a review. Adv. Water Resour. 20, 253–278.Google Scholar
Savage, S. B. & Dai, R. 1993 Studies of granular shear flows: wall slip velocities, ‘layering’, and self-diffusion. Mech. Mater. 16, 225–238.CrossRefGoogle Scholar
Segre, P. N., Liu, F., Umbanhowar, P. & Weitz, D. A. 2001 An effective gravitational temperature for sedimentation. Nature 409, 594–597.Google Scholar
Spalding, D. B. 1980 Numerical computation of multiphase flow and heat-transfer. In Recent Advances in Numerical Methods in Fluids (ed. Taylor, C.). Pinbridge.Google Scholar
Stickel, J. J., Phillips, R. J. & Powell, R. L. 2006 A constitutive model for microstructure and total stress in particulate suspensions. J. Rheol. 50, 379–413.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar
Sun, J. & Sundaresan, S. 2011 A constitutive model with microstructure evolution for flow of rate-independent granular materials. J. Fluid Mech. 682, 590–616.Google Scholar
Sundaresan, S. 2003 Instabilities in fluidized beds. Annu. Rev. Fluid Mech. 35, 63–88.Google Scholar
Syamlal, M. 1998 MFIX documentation: numerical techniques. Tech. Rep. Department of Energy, National Energy Technology Laboratory, see also.Google Scholar
Xu, H., Verberg, R., Koch, D. L. & Louge, M. Y. 2009 Dense, bounded shear flows of agitated solid spheres in a gas at intermediate Stokes and finite Reynolds numbers. J. Fluid Mech. 618, 181–208.Google Scholar