Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T07:09:46.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of non-parallel mean flow on the Green’s function for predicting the low-frequency sound from turbulent air jets

Published online by Cambridge University Press:  13 February 2012

M. E. Goldstein ,
Adrian Sescu  and
M. Z. Afsar
M. E. Goldstein*
Affiliation:
National Aeronautics and Space Administration, Glenn Research Center, Cleveland, OH 44135, USA
Adrian Sescu
Affiliation:
University of Toledo, Department of Mechanical Industrial & Manufacturing Engineering, Toledo, OH 43606, USA
M. Z. Afsar
Affiliation:
National Aeronautics and Space Administration, Glenn Research Center, Cleveland, OH 44135, USA
*
†Email address for correspondence: Marvin.E.Goldstein@nasa.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

It is now well-known that there is an exact formula relating the far-field jet noise spectrum to the convolution product of a propagator (that accounts for the mean flow interactions) and a generalized Reynolds stress autocovariance tensor (that accounts for the turbulence fluctuations). The propagator depends only on the mean flow and an adjoint vector Green’s function for a particular form of the linearized Euler equations. Recent numerical calculations of Karabasov, Bogey & Hynes (AIAA Paper 2011-2929) for a Mach 0.9 jet show use of the true non-parallel flow Green’s function rather than the more conventional locally parallel flow result leads to a significant increase in the predicted low-frequency sound radiation at observation angles close to the downstream jet axis. But the non-parallel flow appears to have little effect on the sound radiated at 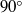to the downstream axis. The present paper is concerned with the effects of non-parallel mean flows on the adjoint vector Green’s function. We obtain a low-frequency asymptotic solution for that function by solving a very simple second-order hyperbolic equation for a composite dependent variable (which is directly proportional to a pressure-like component of this Green’s function and roughly corresponds to the strength of a monopole source within the jet). Our numerical calculations show that this quantity remains fairly close to the corresponding parallel flow result at low Mach numbers and that, as expected, it converges to that result when an appropriately scaled frequency parameter is increased. But the convergence occurs at progressively higher frequencies as the Mach number increases and the supersonic solution never actually converges to the parallel flow result in the vicinity of a critical- layer singularity that occurs in that solution. The dominant contribution to the propagator comes from the radial derivative of a certain component of the adjoint vector Green’s function. The non-parallel flow has a large effect on this quantity, causing it (and, therefore, the radiated sound) to increase at subsonic speeds and decrease at supersonic speeds. The effects of acoustic source location can be visualized by plotting the magnitude of this quantity, as function of position. These ‘altitude plots’ (which represent the intensity of the radiated sound as a function of source location) show that while the parallel flow solutions exhibit a single peak at subsonic speeds (when the source point is centred on the initial shear layer), the non-parallel solutions exhibit a double peak structure, with the second peak occurring about two potential core lengths downstream of the nozzle. These results are qualitatively consistent with the numerical calculations reported in Karabasov et al. (2011).

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 695 , 25 March 2012 , pp. 199 - 234
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Johns Hopkins University, Department of Mechanical Engineering, Baltimore, MD 21218, USA

References

1. Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
2. Afsar, M. Z. 2010 Asymptotic properties of the overall sound pressure level of sub-sonic air jets using isotropy as a paradigm. J. Fluid Mech. 664, 510–539.CrossRefGoogle Scholar
3. Afsar, M. Z. 2012 Insight into the two-source structure of the jet noise spectrum using a generalized shell model of turbulence. Eur. J. Mech. B/Fluids 31, 129–139.CrossRefGoogle Scholar
4. Bodony, D. J. & Lele, S. K. 2008 Low frequency sound sources in high-speed turbulent jets. J. Fluid Mech. 617, 231–253.Google Scholar
5. Bogey, C & Bailly, C. 2010 The influence of nozzle-exit boundary layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–540.CrossRefGoogle Scholar
6. Crocco, L. 1932 Sulla transmission del calore da una lmina piana aun fluido scorrente ad alta velocita. L’Aerotenca 12, 181–197 (translated as NACA TM 690).Google Scholar
7. Freund, J. 2003 Noise source turbulence statistics and the noise from a Mach 0.9 jet. Phys. Fluids 15, 1788–1799.Google Scholar
8. Garabedian, P. R. 1964 Partial Differential Equations. John Wiley.Google Scholar
9. Goldstein, M. E. 1975 The low frequency sound from multipole sources in axysymmetric shear flows with application to jet noise. J. Fluid Mech. 70, 595–604.Google Scholar
10. Goldstein, M. E. 1976 The low frequency sound from multipole sources in axysymmetric shear flows with application to jet noise. Part 2. J. Fluid Mech. 75, 17–28.CrossRefGoogle Scholar
11. Goldstein, M. E. 2003 A generalized acoustic analogy. J. Fluid Mech. 488, 315–333.CrossRefGoogle Scholar
12. Goldstein, M. E. 2006 Hybrid Reynolds-averaged Navier–Stokes/large eddy simulation approach for predicting jet noise. AIAA J. 44 (12), 3136–3142.Google Scholar
13. Goldstein, M. E. 2011 Recent developments in the application of the generalized acoustic analogy to jet noise prediction. Intl J. Aeroacoust. 10 (2&3), 89–116.Google Scholar
14. Goldstein, M. E. & Leib, S. J. 2008a The role of instability waves in predicting jet noise. J. Fluid Mech. 525, 37–72.CrossRefGoogle Scholar
15. Goldstein, M. E. & Leib, S. J. 2008b The aero-acoustics of slowly diverging supersonic jets. J. Fluid Mech. 600, 291–337.CrossRefGoogle Scholar
16. Harper-Bourne, M. 2003 Jet noise measurements. AIAA Paper 2003–3214.Google Scholar
17. Hirsch, C. 2001 Computational Methods for Inviscid and Viscous Flows. John Wiley and Sons, ISBN-10: 0471924520.Google Scholar
18. Howe, M. S. 1970 Transmission of an acoustic pulse through a plane vortex sheet. J. Fluid Mech. 43 (2), 353–367.Google Scholar
19. Karabasov, S. A. 2010 a Once again on the importance of propagation effects for jet noise modelling. AIAA Paper 2010-3966.CrossRefGoogle Scholar
20. Karabasov, S. A. 2010b Understanding jet noise. Phil. Trans. R. Soc. Lond. A 368, 3593–3608.Google Scholar
21. Karabasov, S. A., Afsar, M. Z., Hynes, T. P., Dowling, A. P., McMullan, W. A., Pokora, C. D., Page, G. J. & McGuirk, J. J. 2008 Using large eddy simulation within an acoustic analogy approach for jet noise modeling. AIAA Paper 2008-2985.CrossRefGoogle Scholar
22. Karabasov, S. A., Afsar, M. Z., Hynes, T. P., Dowling, A. P., McMullan, W. A., Pokora, C. D., Page, G. J. & McGuirk, J. J. 2010 Jet noise: acoustic analogy informed by large eddy simulation. AIAA J. 48 (7), 1312–1325.Google Scholar
23. Karabasov, S. A., Bogey, C & Hynes, T. P. 2011 Computation of noise of initially laminar jets using a statistical approach for the acoustic analogy: application and discussion. AIAA Paper 2011-2929.Google Scholar
24. Karabasov, S. A., Hynes, T. P. & Dowling, A. P. 2007 Effect of mean flow evolution on sound propagation through non-uniform mean flows. AIAA Paper 2007-3655.CrossRefGoogle Scholar
25. Khavaran, A., Bridges, J. & Georgiadis, N. 2005 Prediction of turbulence-generated noise in unheated jets. NASA TM 2005-213827.Google Scholar
26. Lighthill, M. J. 1952 On sound generated aerodynamically. I. General theory. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
27. Lighthill, M. J. 1954 On sound generated aerodynamically. II. Turbulence as a source of sound. Proc. R. Soc. Lond. A 222, 1–32.Google Scholar
28. Lighthill, M. J. 1963 ‘Jet noise’ – the 1963 Wright brothers lecture. AIAA J. 1, 1507–1517.CrossRefGoogle Scholar
29. Lilley, G. M. 1972 Generation of sound in a mixing region. Lockheed Aircraft Co. 4th Monthly progress report on contract F-33615-71-C-1663, Marietta.Google Scholar
30. McMullen, W. A., Pokora, C. D., Page, g. j. & McGuirk, j. j. 2008 Large eddy simulation of a high Reynolds number subsonic turbulent jet for acoustic source capture. AIAA Paper 2008-2974.Google Scholar
31. Morse, P. M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw-Hill.Google Scholar
32. Pokora, C. D & McGuirk, J. J. 2008Spatio-temporal turbulence correlations using high speed PIV in an axi-symmetric jet. AIAA Paper 2008-3028.Google Scholar
33. Sokolnikoff, I. S. & Redheffer, R. M. 1958 Mathematics of Physics and Modern Engineering. McGraw-Hill.CrossRefGoogle Scholar
34. Suzuki, T. & Lele, S. K. 2003 Green’s functions for a source in a boundary layer: direct waves, channeled waves and diffracted waves. J. Fluid Mech. 477, 129–173.Google Scholar
35. Tam, C. K. W. & Auriault, L. 1998 Mean flow refraction effects on sound from localized sources in a jet. J. Fluid Mech. 370, 149–174.CrossRefGoogle Scholar
36. Tam, C. K. W. & Burton, D. E 1984 Sound generated by instability waves in supersonic flows. Part 2. J. Fluid Mech. 138, 273–295.CrossRefGoogle Scholar
37. Tam, C. K. W., Viswanathan, K., Ahuja, K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.CrossRefGoogle Scholar
38. Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic.Google Scholar