Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T13:51:13.360Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects

Published online by Cambridge University Press:  11 May 2016

Peter J. Ireland ,
Andrew D. Bragg  and
Lance R. Collins
Peter J. Ireland
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA International Collaboration for Turbulence Research
Andrew D. Bragg
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA International Collaboration for Turbulence Research
Lance R. Collins*
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA International Collaboration for Turbulence Research
*
†Email address for correspondence: lc246@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In Part 1 of this study (Ireland et al., J. Fluid Mech., vol. 796, 2016, pp. 617–658), we analysed the motion of inertial particles in isotropic turbulence in the absence of gravity using direct numerical simulation (DNS). Here, in Part 2, we introduce gravity and study its effect on single-particle and particle-pair dynamics over a wide range of flow Reynolds numbers, Froude numbers and particle Stokes numbers. The overall goal of this study is to explore the mechanisms affecting particle collisions, and to thereby improve our understanding of droplet interactions in atmospheric clouds. We find that the dynamics of heavy particles falling under gravity can be artificially influenced by the finite domain size and the periodic boundary conditions, and we therefore perform our simulations on larger domains to reduce these effects. We first study single-particle statistics that influence the relative positions and velocities of inertial particles. We see that gravity causes particles to sample the flow more uniformly and reduces the time particles can spend interacting with the underlying turbulence. We also find that gravity tends to increase inertial particle accelerations, and we introduce a model to explain that effect. We then analyse the particle relative velocities and radial distribution functions (RDFs), which are generally seen to be independent of Reynolds number for low and moderate Kolmogorov-scale Stokes numbers 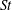$St$. We see that gravity causes particle relative velocities to decrease by reducing the degree of preferential sampling and the importance of path-history interactions, and that the relative velocities have higher scaling exponents with gravity. We observe that gravity has a non-trivial effect on clustering, acting to decrease clustering at low 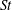$St$ and to increase clustering at high 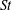$St$. By considering the effect of gravity on the clustering mechanisms described in the theory of Zaichik & Alipchenkov (New J. Phys., vol. 11, 2009, 103018), we provide an explanation for this non-trivial effect of gravity. We also show that when the effects of gravity are accounted for in the theory of Zaichik & Alipchenkov (2009), the results compare favourably with DNS. The relative velocities and RDFs exhibit considerable anisotropy at small separations, and this anisotropy is quantified using spherical harmonic functions. We use the relative velocities and the RDFs to compute the particle collision kernels, and find that the collision kernel remains as it was for the case without gravity, namely nearly independent of Reynolds number for low and moderate 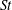$St$. We conclude by discussing practical implications of the results for the cloud physics and turbulence communities and by suggesting possible avenues for future research.

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 659 - 711
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Applied Mathematics and Plasma Physics Group, Los Alamos National Laboratory, Los Alamos, NM 87545, USA.

References

Abrahamson, J. 1975 Collision rates of small particles in a vigorously turbulent fluid. Chem. Engng Sci. 30, 1371–1379.CrossRefGoogle Scholar
Alipchenkov, V. M. & Beketov, A. I. 2013 On clustering of aerosol particles in homogeneous turbulent shear flows. J. Turbul. 14 (5), 1–9.CrossRefGoogle Scholar
Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.CrossRefGoogle Scholar
Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1: results from direct numerical simulation. New J. Phys. 10, 075015.CrossRefGoogle Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97, 144507.CrossRefGoogle ScholarPubMed
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.CrossRefGoogle Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112, 184501.CrossRefGoogle ScholarPubMed
Bragg, A. D. & Collins, L. R. 2014a New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A. D. & Collins, L. R. 2014b New insights from comparing statistical theories for inertial particles in turbulence: II: relative velocities. New J. Phys. 16, 055014.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015a Mechanisms for the clustering of inertial particles in the inertial range of isotropic turbulence. Phys. Rev. E 92, 023029.CrossRefGoogle ScholarPubMed
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015b On the relationship between the non-local clustering mechanism and preferential concentration. J. Fluid Mech. 780, 327–343.CrossRefGoogle Scholar
Chun, J., Koch, D. L., Rani, S., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops, and Particles. Academic.Google Scholar
Computational and Information Systems Laboratory 2012 Yellowstone: IBM iDataPlex System (University Community Computing) http://n2t.net/ark:/85065/d7wd3xhc.Google Scholar
Corrsin, S. 1963 Estimates of the relations between Eulerian and Lagrangian scales in large Reynolds number turbulence. J. Atmos. Sci. 20, 115–119.2.0.CO;2>CrossRefGoogle Scholar
Csanady, G. T. 1963 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 20, 201–208.2.0.CO;2>CrossRefGoogle Scholar
Dávila, J. & Hunt, J. C. R. 2001 Settling of small particles near vortices and in turbulence. J. Fluid Mech. 440, 117–145.CrossRefGoogle Scholar
Dejoan, A. & Monchaux, R. 2013 Preferential concentration and settling of heavy particles in homogeneous turbulence. Phys. Fluids 25, 013301.CrossRefGoogle Scholar
Devenish, B. J., Bartello, P., Brenguier, J.-L., Collins, L. R., Grabowski, W. W., IJzermans, R. H. A., Malinowski, S. P., Reeks, M. W., Vassilicos, J. C., Wang, L.-P. et al. 2012 Droplet growth in warm turbulent clouds. Q. J. R. Meteorol. Soc. 138, 1401–1429.CrossRefGoogle Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.CrossRefGoogle Scholar
Elghobashi, S. E. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 242, 655–700.CrossRefGoogle Scholar
Elghobashi, S. E. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed particles. I: turbulence modification. Phys. Fluids A 5, 1790–1801.CrossRefGoogle Scholar
Fouxon, I., Park, Y., Harduf, R. & Lee, C. 2015 Inhomogeneous distribution of water droplets in cloud turbulence. Phys. Rev. E 92, 033001.Google ScholarPubMed
Franklin, C. N., Vaillancourt, P. A. & Yau, M. K. 2007 Statistics and parameterizations of the effect of turbulence on the geometric collision kernel of cloud droplets. J. Atmos. Sci. 64, 938–954.CrossRefGoogle Scholar
Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 255–281.CrossRefGoogle Scholar
Ghosh, S., Dávila, J., Hunt, J. C. R., Srdic, A., Fernando, H. H. S. & Jonas, P. R. 2005 How turbulence enhances coalescence of settling particles with applications to rain in clouds. Proc. R. Soc. Lond. A 461, 3059–3088.Google Scholar
Good, G. H., Ireland, P. J., Bewley, G. P., Bodenschatz, E., Collins, L. R. & Warhaft, Z. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.CrossRefGoogle Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.CrossRefGoogle Scholar
Gualtieri, P., Picano, F. & Casciola, C. M. 2009 Anisotropic clustering of inertial particles in homogeneous shear flow. J. Fluid Mech. 629, 25–39.CrossRefGoogle Scholar
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112, 214501.Google Scholar
van Hinsberg, M. A. T., Thije Boonkkamp, J. H. M., Toschi, F. & Clercx, H. J. H. 2012 On the efficiency and accuracy of interpolation methods for spectral codes. SIAM J. Sci. Comput. 34 (4), B479–B498.CrossRefGoogle Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.CrossRefGoogle Scholar
Ireland, P. J. & Collins, L. R. 2012 Direct numerical simulation of inertial particle entrainment in a shearless mixing layer. J. Fluid Mech. 704, 301–332.CrossRefGoogle Scholar
Ireland, P. J., Vaithianathan, T., Sukheswalla, P. S., Ray, B. & Collins, L. R. 2013 Highly parallel particle-laden flow solver for turbulence research. Comput. Fluids 76, 170–177.CrossRefGoogle Scholar
Kawanisi, K. & Shiozaki, R. 2008 Turbulent effects on the settling velocity of suspended sediment. J. Hydraul. Engng 134, 261–266.CrossRefGoogle Scholar
Lavezzo, V., Soldati, A., Gerashchenko, S., Warhaft, Z. & Collins, L. R. 2010 On the role of gravity and shear on the acceleration of inertial particles in near-wall turbulence. J. Fluid Mech. 658, 229–246.CrossRefGoogle Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
Nielsen, P. 1993 Turbulence effects on the settling of suspended particles. J. Sedim. Petrol. 63, 835–838.Google Scholar
Onishi, R., Takahashi, K. & Komori, S. 2009 Influence of gravity on collisions of monodispersed droplets in homogeneous isotropic turbulence. Phys. Fluids 21, 125108.CrossRefGoogle Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.CrossRefGoogle Scholar
Parishani, H., Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2015 Effects of gravity on the acceleration and pair statistics of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 27, 033304.CrossRefGoogle Scholar
Park, Y. & Lee, C. 2014 Gravity-driven clustering of inertial particles in turbulence. Phys. Rev. E 89, 061004(R).Google ScholarPubMed
Pinsky, M. B., Khain, A. P. & Shapiro, M. 2007 Collisions of cloud droplets in a turbulent flow. Part IV: droplet hydrodynamic interaction. J. Atmos. Sci. 64, 2462–2482.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitation. Kluwer.Google Scholar
Reade, W. C. & Collins, L. R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12, 2530–2540.CrossRefGoogle Scholar
Reeks, M. W. 1993 On the constitutive relations for dispersed particles in nonuniform flows. I: dispersion in a simple shear flow. Phys. Fluids A 5, 750–761.CrossRefGoogle Scholar
Rosa, B., Parishani, H., Ayala, O., Grabowski, W. W. & Wang, L. P. 2013 Kinematic and dynamic collision statistics of cloud droplets from high-resolution simulations. New J. Phys. 15, 045032.CrossRefGoogle Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012 Inertial particle acceleration statistics in turbulence: effects of filtering, biased sampling, and flow topology. Phys. Fluids 24, 083302.CrossRefGoogle Scholar
Shaw, R. A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic, particle-laden turbulent suspension I. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. R. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.CrossRefGoogle Scholar
Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008a Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237, 2084–2089.CrossRefGoogle Scholar
Volk, R., Mordant, N., Verhille, G. & Pinton, J.-F. 2008b Laser Doppler measurement of inertial particle and bubble accelerations in turbulence. Eur. Phys. Lett. 81, 34002.CrossRefGoogle Scholar
Voßkuhle, M., Pumir, A., Lévêque, E. & Wilkinson, M. 2014 Prevalence of the sling effect for enhancing collision rates in turbulent suspensions. J. Fluid Mech. 749, 841–852.CrossRefGoogle Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.CrossRefGoogle Scholar
Wang, L.-P. & Stock, D. E. 1993 Dispersion of heavy particles by turbulent motion. J. Atmos. Sci. 50, 1897–1913.2.0.CO;2>CrossRefGoogle Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modeling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.CrossRefGoogle Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.CrossRefGoogle Scholar
Wilkinson, M., Mehlig, B. & Bezuglyy, V. 2006 Caustic activation of rain showers. Phys. Rev. Lett. 97, 048501.CrossRefGoogle ScholarPubMed
Woittiez, E. J. P., Jonker, H. J. J. & Portela, L. M. 2009 On the combined effects of turbulence and gravity on droplet collisions in clouds: a numerical study. J. Atmos. Sci. 66, 1926–1943.CrossRefGoogle Scholar
Yang, C. Y. & Lei, U. 1998 The role of turbulent scales in the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 20, 179–205.CrossRefGoogle Scholar
Yang, T. S. & Shy, S. S. 2003 The settling velocity of heavy particles in an aqueous near-isotropic turbulence. Phys. Fluids 15, 868–880.CrossRefGoogle Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.CrossRefGoogle Scholar
Yudine, M. I. 1959 Physical considerations on heavy-particle dispersion. Adv. Geophys. 6, 185–191.CrossRefGoogle Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2008 Acceleration of heavy particles in isotropic turbulence. Intl J. Multiphase Flow 34 (9), 865–868.CrossRefGoogle Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.CrossRefGoogle Scholar