Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T06:35:52.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of spatial discretization of energy on detonation wave propagation

Published online by Cambridge University Press:  16 March 2017

XiaoCheng Mi Open the ORCID record for XiaoCheng Mi [Opens in a new window] ,
Evgeny V. Timofeev  and
Andrew J. Higgins
XiaoCheng Mi
Affiliation:
McGill University, Department of Mechanical Engineering, Montreal, Quebec H3A 0G4, Canada
Evgeny V. Timofeev
Affiliation:
McGill University, Department of Mechanical Engineering, Montreal, Quebec H3A 0G4, Canada
Andrew J. Higgins*
Affiliation:
McGill University, Department of Mechanical Engineering, Montreal, Quebec H3A 0G4, Canada
*
†Email address for correspondence: andrew.higgins@mcgill.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Detonation propagation in the limit of highly spatially discretized energy sources is investigated. The model of this problem begins with a medium consisting of a calorically perfect gas with a prescribed energy release per unit mass. The energy release is collected into sheet-like sources that are embedded in an inert gas that fills the spaces between them. The release of energy in the first sheet results in a planar blast wave that propagates to the next source, which is triggered after a prescribed delay, generating a new blast, and so forth. The resulting wave dynamics as the front passes through hundreds of such sources is computationally simulated by numerically solving the governing one-dimensional Euler equations in the laboratory-fixed reference frame. Two different solvers are used: one with a fixed uniform grid and the other using an unstructured, adaptively refined grid enabling the limit of highly concentrated, spatially discrete sources to be examined. The two different solvers generate consistent results, agreeing within the accuracy of the measured wave speeds. The average wave speed for each simulation is measured once the wave propagation has reached a quasi-periodic solution. The effect of source delay time, source energy density, specific heat ratio and the spatial discreteness of the sources on the wave speed is studied. Sources fixed in the laboratory reference frame versus sources that convect with the flow are compared. Simulations using an Arrhenius-rate-dependent energy release are performed as well. The average wave speed is compared to the ideal Chapman–Jouguet (CJ) speed of the equivalent homogenized media. Velocities in excess of the CJ speed are found as the sources are made increasingly discrete, with the deviation above CJ being as great as 15 %. The deviation above the CJ value increases with decreasing values of specific heat ratio 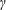$\unicode[STIX]{x1D6FE}$ . The total energy release, delay time and whether the sources remain laboratory-fixed or are convected with the flow do not have a significant influence on the deviation of the average wave speed away from CJ. A simple, ad hoc analytic model is proposed to treat the case of zero delay time (i.e. source energy released at the shock front) that exhibits qualitative agreement with the computational solutions and may explain why the deviation from CJ increases with decreasing 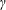$\unicode[STIX]{x1D6FE}$ . When the sources are sufficiently spread out so as to make the energy release of the media nearly continuous, the classic CJ solution is obtained for the average wave speed. Such continuous waves can also be shown to have a time-averaged structure consistent with the classical Zel’dovich–von Neumann–Döring (ZND) structure of a detonation. In the limit of highly discrete sources, temporal averaging of the wave structure shows that the effective sonic surface does not correspond to an equilibrium state. The average state of the flow leaving the wave in this case does eventually reach the equilibrium Hugoniot, but only after the effective sonic surface has been crossed. Thus, the super-CJ waves observed in the limit of highly discretized sources can be understood as weak detonations due to the non-equilibrium state at the effective sonic surface. These results have implications for the validity of the CJ criterion as applied to highly unstable detonations in gases and heterogeneous detonations in condensed phase and multiphase media.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 817 , 25 April 2017 , pp. 306 - 338
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. B. & Long, L. N. 2003 Direct monte carlo simulation of chemical reaction systems: prediction of ultrafast detonations. J. Chem. Phys. 118 (7), 3102–3110.Google Scholar
Beck, J. M. & Volpert, V. A. 2003 Nonlinear dynamics in a simple model of solid flame microstructure. Physica D 182 (12), 86–102.CrossRefGoogle Scholar
Brode, H. L. 1955 Numerical solutions of spherical blast waves. J. Appl. Phys. 26 (6), 766–775.Google Scholar
Buckmaster, J. & Neves, J. 1988 One-dimensional detonation stability: the spectrum for infinite activation energy. Phys. Fluids 31 (12), 3571–3576.Google Scholar
Chapman, D. L. 1899 On the rate of explosion in gases. Phil. Mag. 47 (284), 90–104.Google Scholar
Chernyi, G. G. 1961 Introduction to Hypersonic Flow. Academic.Google Scholar
Clavin, P. & He, L. 1996 Stability and nonlinear dynamics of one-dimensional overdriven detonations in gases. J. Fluid Mech. 306, 353–378.Google Scholar
Clavin, P., He, L. & Williams, F. A. 1997 Multidimensional stability analysis of overdriven gaseous detonations. Phys. Fluids 9 (12), 3764–3785.Google Scholar
Dabora, E. K., Ragland, K. W. & Nicholls, J. A. 1969 Drop-size effects in spray detonations. In Symposium (International) on Combustion, vol. 12, pp. 19–26. The Combustion Institute.Google Scholar
Davis, W. C. 1987 The detonation of explosives. Sci. Am. 256, 106–112.Google Scholar
Denisov, Yu. N. & Troshin, Ya. K. 1961 On the mechanism of detonative combustion. In Eighth Symposium (International) on Combustion, vol. 8, pp. 600–610. The Combustion Institute.Google Scholar
Erpenbeck, J. J. 1964 Stability of idealized one-reaction detonations. Phys. Fluids 7 (5), 684–696.CrossRefGoogle Scholar
Erpenbeck, J. J. 1965 Stability of idealized one-reaction detonations: zero activation energy. Phys. Fluids 8 (6), 1192–1193.Google Scholar
Eyring, H., Powell, R. E., Duffy, G. H. & Parlin, R. B. 1949 The stability of detonation. Chem. Rev. 45 (1), 69–181.CrossRefGoogle Scholar
Faria, L. M. & Kasimov, A. R. 2015 Qualitative modeling of the dynamics of detonations with losses. Proc. Combust. Inst. 35 (2), 2015–2023.CrossRefGoogle Scholar
Fickett, W. & Davis, W. C. 2000 Detonation: Theory and Experiment. Dover.Google Scholar
Gao, Y., Ng, H. D. & Lee, J. H. 2015 Experimental characterization of galloping detonations in unstable mixtures. Combust. Flame 162 (6), 2405–2413.CrossRefGoogle Scholar
Gois, J. C., Campos, J. & Mendes, R. 1996 Extinction and initiation of detonation of NM-PMMA-GMB mixtures. AIP Conf. Proc. 370 (1), 827–830.CrossRefGoogle Scholar
Goroshin, S., Lee, J. H. S. & Shoshin, Yu. 1998 Effect of the discrete nature of heat sources on flame propagation in particulate suspensions. Proc. Combust. Inst. 27 (1), 743–749.Google Scholar
Goroshin, S., Tang, F. D. & Higgins, A. J. 2011 Reaction-diffusion fronts in media with spatially discrete sources. Phys. Rev. E 84 (2), 027301.Google Scholar
Higgins, A. J. 2009 Measurement of detonation velocity for a nonideal heterogeneous explosive in axisymmetric and two-dimensional geometries. AIP Conf. Proc. 1195, 193–196.Google Scholar
Higgins, A. J. 2012 Steady one-dimensional detonations. In Shock Waves Science and Technology Library (ed. Zhang, F.), Shock Wave Science and Technology Reference Library, vol. 6, pp. 33–105. Springer.CrossRefGoogle Scholar
Higgins, A. J. 2014 Discrete effects in energetic materials. J. Phys.: Conf. Ser. 500 (5), 052016.Google Scholar
Jackson, S. I., Lee, B. J. & Shepherd, J. E. 2015 Detonation mode and frequency variation under high loss conditions. In 25th International Colloquium on the Dynamics of Explosions and Reactive Systems. Paper 134. http://www.icders.org/ICDERS2015/abstracts/ICDERS2015-134.pdf.Google Scholar
Jones, D. L. 1961 Strong blast waves in spherical, cylindrical, and plane shocks. Phys. Fluids 4 (9), 1183–1184.Google Scholar
Jouguet, E 1905 Sur la propagation des réactions chimiques dans les gaz. J. Mathé. Pures Appl. 1, 347–425.Google Scholar
Kasimov, A. R., Faria, L. M. & Rosales, R. R. 2013 Model for shock wave chaos. Phys. Rev. Lett. 110 (10), 104104.Google Scholar
Kasimov, A. R. & Stewart, D. S. 2004 On the dynamics of self-sustained one-dimensional detonations: a numerical study in the shock-attached frame. Phys. Fluids 16 (10), 3566–3578.CrossRefGoogle Scholar
Kiyanda, C. B. & Higgins, A. J. 2013 Photographic investigation into the mechanism of combustion in irregular detonation waves. Shock Waves 23 (2), 115–130.CrossRefGoogle Scholar
Lee, J. H. S. 2003 The universal role of turbulence in the propagation of strong shocks and detonation waves. In High-Pressure Shock Compression of Solids VI, pp. 121–148. Springer.Google Scholar
Lee, J. H. S. & Radulescu, M. I. 2005 On the hydrodynamic thickness of cellular detonations. Combust. Explos. Shock Waves 41 (6), 745–765.Google Scholar
Lee, J. J., Dupré, G., Knystautas, R. & Lee, J. H. 1995 Doppler interferometry study of unstable detonations. Shock Waves 5 (3), 175–181.Google Scholar
Lefebvre, M. H., Nzeyimana, E. & van Tiggelen, P. J. 1993 Influence of fluorocarbons on H2O2Ar detonation: experiments and modeling. In Prog. Astronaut. Aeronaut., vol. 153, pp. 144–161.Google Scholar
Leung, C., Radulescu, M. I. & Sharpe, G. J. 2010 Characteristics analysis of the one-dimensional pulsating dynamics of chain-branching detonations. Phys. Fluids 22 (12), 126101.CrossRefGoogle Scholar
Li, J., Mi, X. & Higgins, A. J. 2015 Effect of spatial heterogeneity on near-limit propagation of a pressure-dependent detonation. Proc. Combust. Inst. 35 (2), 2025–2032.Google Scholar
Majda, A. 1981 A qualitative model for dynamic combustion. SIAM J. Appl. Maths 41 (1), 70–93.CrossRefGoogle Scholar
Mcvey, J. B. & Toong, T. Y. 1971 Mechanism of instabilities of exothermic hypersonic blunt-body flows. Combust. Sci. Technol. 3 (2), 63–76.Google Scholar
Mi, X. & Higgins, A. J. 2015 Influence of discrete sources on detonation propagation in a Burgers equation analog system. Phys. Rev. E 91, 053014.Google Scholar
Mi, X., Higgins, A. J., Goroshin, S. & Bergthorson, J. M. 2017 The influence of spatial discreteness on the thermo-diffusive instability of flame propagation with infinite lewis number. Proc. Combust. Inst. 36 (2), 2359–2366.Google Scholar
Morano, E. O. & Shepherd, J. E. 2002 Effect of reaction rate periodicity on detonation propagation. AIP Conf. Proc. 620 (1), 446–449.Google Scholar
von Neumann, J.1942 Theory of detonation waves. Tech. Rep. OSRD-549. National Defense Research Committee.Google Scholar
Ng, H. D. & Zhang, F. 2012 Detonation instability. In Shock Waves Science and Technology Library, vol. 6, pp. 107–212. Springer.Google Scholar
Oppenheim, A. K. 1961 Development and structure of plane detonation waves. In Fourth AGARD Combustion and Propulsion Colloquium, pp. 186–258. The Combustion Institute.Google Scholar
Petel, O. E., Mack, D., Higgins, A. J., Turcotte, R. & Chan, S. K. 2006 Comparison of the detonation failure mechanism in homogeneous and heterogeneous explosives. In 13th Symposium (International) on Detonation, pp. 2–11. Office of Naval Research.Google Scholar
Petel, O. E., Mack, D., Higgins, A. J., Turcotte, R. & Chan, S. K. 2007 Minimum propagation diameter and thickness of high explosives. J. Loss Prev. Process. Ind. 20 (4–6), 578–583.Google Scholar
Pierce, T. H. & Nicholls, J. A. 1973 Time variation in the reaction-zone structure of two-phase spray detonations. In Symposium (International) on Combustion, vol. 14, (1), pp. 1277–1284. The Combustion Institute.Google Scholar
Radulescu, M. I., Sharpe, G. J., Law, C. K. & Lee, J. H. S. 2007 The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.CrossRefGoogle Scholar
Radulescu, M. I. & Shepherd, J. E. 2015 Dynamics of galloping detonations: inert hydrodynamics with pulsed energy release. Bull. Am. Phys. Soc. 60. http://adsabs.harvard.edu/abs/2015APS..DFD.R2006R.Google Scholar
Radulescu, M. I. & Tang, J. 2011 Nonlinear dynamics of self-sustained supersonic reaction waves: Ficketts detonation analogue. Phys. Rev. Lett. 107 (16), 164503.Google Scholar
Saito, T., Voinovich, P., Timofeev, E. & Takayama, K. 2001 Development and application of high-resolution adaptive numerical techniques in shock wave research center. In Godunov Methods (ed. Toro, E. F.), pp. 763–784. Springer.Google Scholar
Sakurai, A. 1974 Blast wave from a plane source at an interface. J. Phys. Soc. Japan 36 (2), 610–610.Google Scholar
Short, M. 1996 An asymptotic derivation of the linear stability of the square-wave detonation using the Newtonian limit. Proc. R. Soc. Lond. A 452 (1953), 2203–2224.Google Scholar
Short, M. 1997 Multidimensional linear stability of a detonation wave at high activation energy. SIAM J. Appl. Maths 57 (2), 307–326.CrossRefGoogle Scholar
Short, M. & Stewart, D. S. 1998 Cellular detonation stability: a normal mode linear analysis. J. Fluid Mech. 368, 229–262.Google Scholar
Short, M. & Stewart, D. S. 1999 The multi-dimensional stability of weak-heat-release detonations. J. Fluid Mech. 382, 109–135.Google Scholar
Sow, A., Chinnayya, A. & Hadjadj, A. 2014 Mean structure of one-dimensional unstable detonations with friction. J. Fluid Mech. 743, 503–533.Google Scholar
Stewart, D. S. & Asay, B. W. 1991 Discrete modeling of beds of propellant exposed to strong stimulus. In Dynamical Issues in Combustion Theory (ed. Fife, P. C., Liñán, A. & Williams, F. A.), The IMA Volumes in Mathematics and its Applications, vol. 35, pp. 241–257. Springer.Google Scholar
Strang, G. 1968 On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5 (3), 506–517.CrossRefGoogle Scholar
Strehlow, R. A. 1968 Gas phase detonations: Recent developments. Combust. Flame 12 (2), 81–101.Google Scholar
Strehlow, R. A. 1969 The nature of transverse waves in detonations. Astron. Acta 14, 539–548.Google Scholar
Tang, F. D., Higgins, A. J. & Goroshin, S. 2009 Effect of discreteness on heterogeneous flames: propagation limits in regular and random particle arrays. Combust. Theor. Model. 13 (2), 319–341.Google Scholar
Tang, F. D., Higgins, A. J. & Goroshin, S. 2012 Propagation limits and velocity of reaction-diffusion fronts in a system of discrete random sources. Phys. Rev. E 85, 036311.Google Scholar
Tang, J. & Radulescu, M. I. 2013 Dynamics of shock induced ignition in Fickett’s model: influence of 𝜒. Proc. Combust. Inst. 34 (2), 2035–2041.Google Scholar
Toro, E. F. 2009 Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd edn. pp. 182–183. Springer.Google Scholar
Vandermeiren, M. & van Tiggelen, P. J. 1988 Role of an inhibitor on the onset of gas detonations in acetylene mixtures. Prog. Astronaut. Aeronaut. 114, 186–200.Google Scholar
Vasil’ev, A. A. & Nikolaev, Yu. 1978 Closed theoretical model of a detonation cell. Acta Astron. 5 (11-12), 983–996.Google Scholar
White, D. R. 1961 Turbulent structure of gaseous detonation. Phys. Fluids 4 (4), 465–480.Google Scholar
Wood, W. W. & Kirkwood, J. G. 1954 Diameter effect in condensed explosives. The relation between velocity and radius of curvature of the detonation wave. J. Chem. Phys. 22 (11), 1920–1924.Google Scholar