Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-27T12:32:24.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of viscoelasticity on the soft-wall transition and turbulence in a microchannel

Published online by Cambridge University Press:  12 January 2017

S. S. Srinivas  and
V. Kumaran
S. S. Srinivas
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: kumaran@chemeng.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The modification of soft-wall turbulence in a microchannel due to small amounts of polymer dissolved in water is experimentally studied. The microchannels are of rectangular cross-section with height 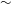${\sim}$160 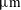$\unicode[STIX]{x03BC}\text{m}$, width 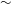${\sim}$1.5 mm and length 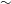${\sim}$3 cm, with three walls made of hard polydimethylsiloxane (PDMS) gel, and one wall made of soft PDMS gel with an elasticity modulus of 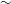${\sim}$18 kPa. Solutions of polyacrylamide of molecular weight 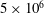$5\times 10^{6}$ and mass fraction up to 50 ppm, and of molecular weight 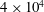$4\times 10^{4}$ and mass fraction up to 1500 ppm, are used in the experiments. In all cases, the solutions are in the dilute limit below the critical overlap concentration, and the solution viscosity does not exceed that of water by more than 10 %. Two distinct types of flow modifications are observed below and above a threshold mass fraction for the polymer, 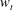$w_{t}$, which is 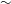${\sim}$1 ppm and 500 ppm for the solutions of polyacrylamide with molecular weights 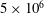$5\times 10^{6}$ and 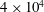$4\times 10^{4}$, respectively. At or below 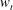$w_{t}$, there is no change in the transition Reynolds number, but there is significant turbulence attenuation, by up to a factor of 2 in the root-mean-square velocities and a factor of 4 in the Reynolds stress. When the polymer concentration increases beyond 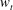$w_{t}$, there is a decrease in the transition Reynolds number and in the intensity of the turbulent fluctuations. The lowest transition Reynolds number is ${\sim}$35 for the solution of polyacrylamide with molecular weight 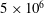$5\times 10^{6}$ and mass fraction 50 ppm (in contrast to 260–290 for pure water). The fluctuating velocities in the streamwise and cross-stream directions are lower by a factor of 5, and the Reynolds stress is lower by a factor of 10, in comparison to pure water.

JFM classification

Complex Fluids: Complex Fluids Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 1076 - 1118
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bohdanecky, M., Petrus, V. & Sedldtek, B. 1983 Estimation of the characteristic ratio of polyacrylamide in water and in a mixed theta-solvent. Makromol. Chem. 184, 2061–2073.CrossRefGoogle Scholar
Chokshi, P., Bhade, P. & Kumaran, V. 2015 Wall-mode instability in plane shear flow of viscoelastic fluid over a deformable solid. Phys. Rev. E 91, 023007.Google Scholar
Chokshi, P. P. & Kumaran, V. 2007 Stability of the flow of a viscoelastic fluid past a deformable surface in the low Reynolds number limit. Phys. Fluids 19, 104103.Google Scholar
Chokshi, P. P. & Kumaran, V. 2008 Weakly nonlinear analysis of viscous instability in flow past a neo-Hookean surface. Phys. Rev. E 77, 056303.Google Scholar
Chokshi, P. P. & Kumaran, V. 2009 Weakly nonlinear stability analysis of a flow past a neo-Hookean solid at arbitrary Reynolds numbers. Phys. Fluids 21, 014109.Google Scholar
Doi, M. & Edwards, S. F. 1988 The Theory of Polymer Dynamics. Oxford Science Publications.Google Scholar
Eggert, M. D. & Kumar, S. 2004 Observations of instability, hysteresis and oscillations in low-Reynolds-number flow past polymer gels. J. Colloid Interface Sci. 274, 238–242.Google Scholar
Gaurav & Shankar, V. 2009 Stability of fluid flow through deformable neo-Hookean tubes. J. Fluid Mech. 627, 291–322.Google Scholar
Gaurav & Shankar, V. 2010 Stability of pressure-driven flow in a deformable neo-Hookean channel. J. Fluid Mech. 659, 318–350.Google Scholar
de Gennes, P. G. 1976 Dynamics of entangled polymers solutions. I. The Rouse model. Macromolecules 9, 587–593.Google Scholar
Gkanis, V. & Kumar, S. 2003 Instability of creeping Couette flow past a neo-Hookean solid. Phys. Fluids 15, 2864–2871.Google Scholar
Gkanis, V. & Kumar, S. 2005 Stability of pressure driven creeping flows in channels lined with a nonlinear elastic solid. J. Fluid Mech. 524, 357–375.Google Scholar
Graham, M. D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26, 101301.CrossRefGoogle Scholar
Hatzikiriakos, S. G. & Vlassopoulos, D. 1996 Brownian dynamics simulations of shear-thickening in dilute polymer solutions. Rheol. Acta 35, 274–287.Google Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71, 39–50.Google Scholar
Kulicke, W.-M., Kniewske, R. & Klein, J. 1982 Preparation, characterisation, solution properties and rheological behaviour of polyacrylamide. Prog. Polym. Sci. 8, 373–468.Google Scholar
Kumaran, V. 1995 Stability of the viscous flow of a fluid through a flexible tube. J. Fluid Mech. 294, 259–281.CrossRefGoogle Scholar
Kumaran, V. 1996 Stability of an inviscid flow in a flexible tube. J. Fluid Mech. 320, 1–17.Google Scholar
Kumaran, V. 1998 Stability of wall modes in a flexible tube. J. Fluid Mech. 362, 1–15.Google Scholar
Kumaran, V. 2000 Classification of instabilities in the flow past flexible surfaces. Curr. Sci. 79, 766–773.Google Scholar
Kumaran, V. 2003 Hydrodynamic stability of flow through compliant channels and tubes. In Proceedings of IUTAM Symposium on Flow in Collapsible Tubes and Past Other Highly Compliant Boundaries (ed. Carpenter, P. W. & Pedley, T. J.). Kluwer Academic Publishers.Google Scholar
Kumaran, V. 2015 Experimental studies on the flow through soft tubes and channels. Sadhana 40, 911–923.Google Scholar
Kumaran, V. & Bandaru, P. 2016 Ultra-fast microfluidic mixing by soft-wall turbulence. Chem. Engng Sci. 149, 156–168.Google Scholar
Kumaran, V., Fredrickson, G. H. & Pincus, P. 1994 Flow induced instability at the interface between a fluid and a gel at low Reynolds number. J. Phys. France II 4, 893–911.Google Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84, 3310–3313.Google Scholar
Lahav, J., Eliezer, N. & Silberberg, A. 1973 Gel-walled cylindrical channels as models for the microcirculation: dynamics of flow. Biorheology 10, 595–604.Google Scholar
Larson, R. G., Shaqfeh, E. S. G. & Muller, S. J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 218, 573–600.Google Scholar
Lee, M. G., Choi, S. & Park, J.-K. 2010 Rapid multivortex mixing in an alternately formed contraction–expansion array microchannel. Biomed. Microdevices 12, 1019–1026.Google Scholar
Lenzmann, F., Li, K., Kitai, A. H. & Stover, H. D. H. 1994 Thin-film micropatterning using polymer microspheres. Chem. Mater. 6, 156–159.Google Scholar
Morozov, A. N. & van Saarloos, W. 2005 Subcritical finite-amplitude solutions for plane couette flow of viscoelastic fluids. Phys. Rev. Lett. 95, 024501.Google Scholar
Muralikrishnan, R. & Kumaran, V. 2002 Experimental study of the instability of the viscous flow past a flexible surface. Phys. Fluids 14, 775–780.Google Scholar
Neelamegam, R., Shankar, V. & Das, D. 2013 Suppression of purely elastic instabilities in the torsional flow of a viscoelastic liquid past a soft solid. Phys. Fluids 25, 124102.Google Scholar
Pan, L., Morozov, A., Wagner, C. & Arratia, P. E. 2013 Nonlinear elastic instability in channel flows at low Reynolds numbers. Phys. Rev. Lett. 110, 174502.CrossRefGoogle ScholarPubMed
Poole, R. J., Escudier, M. P., Afonso, A. & Pinho, F. T. 2007 Laminar flow of a viscoelastic shear-thinning liquid over a backward-facing step preceded by a gradual contraction. Phys. Fluids 19, 093101.Google Scholar
Sadanandan, B. & Sureshkumar, R. 2002 Viscoelastic effects on the stability of wall-bounded shear flows. Phys. Fluids 14, 41–48.Google Scholar
Samanta, D., Dubief, Y., Holzner, M., Schfer, C., Morozov, A. N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110, 10557–10562.Google Scholar
Shankar, V. 2015 Stability of fluid flow through deformable tubes and channels: an overview. Sadhana 40, 925–943.Google Scholar
Shankar, V. & Kumar, S. 2004 Instability of viscoelastic plane couette flow past a deformable wall. J. Non-Newtonian Fluid Mech. 116, 371–393.Google Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flows in a flexible tube. J. Fluid Mech. 395, 211–236.Google Scholar
Shankar, V. & Kumaran, V. 2000 Stability of non-axisymmetric modes in a flexible tube. J. Fluid Mech. 407, 291–314.Google Scholar
Shankar, V. & Kumaran, V. 2001a Asymptotic analysis of wall modes in a flexible tube revisited. Eur. Phys. J. B 19, 607–622.Google Scholar
Shankar, V. & Kumaran, V. 2001b Weakly nonlinear stability of viscous flow past a flexible surface. J. Fluid Mech. 434, 337–354.Google Scholar
Shankar, V. & Kumaran, V. 2002 Stability of wall modes in the flow past a flexible surface. Phys. Fluids 14, 2324–2338.CrossRefGoogle Scholar
Shrivastava, A., Cussler, E. L. & Kumar, S. 2008 Mass transfer enhancement due to a soft boundary. Chem. Engng Sci. 63, 4302–4305.Google Scholar
Srinivas, S. S. & Kumaran, V. 2015 After transition in a soft-walled microchannel. J. Fluid Mech. 780, 649–686.Google Scholar
Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.Google Scholar
Toms, B. A. 1977 On the early experiments on drag reduction by polymers. Phys. Fluids 20, S3–S8.Google Scholar
Verma, M. K. S. & Kumaran, V. 2012 A dynamical instability due to fluid–wall coupling lowers the transition Reynolds number in the flow through a flexible tube. J. Fluid Mech. 705, 322–347.Google Scholar
Verma, M. K. S. & Kumaran, V. 2013 A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall. J. Fluid Mech. 727, 407–455.Google Scholar
Verma, M. K. S. & Kumaran, V. 2015 Stability of the flow in a soft tube deformed due to an applied pressure gradient. Phys. Rev. E 91, 043001.Google Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21, 625–656.Google Scholar
Wang, S.-N., Graham, M. D., Hahn, F. J. & Xi, L. 2014 Time-series and extended Karhunen–Loève analysis of turbulent drag reduction in polymer solutions. AIChE J. 60, 1460–1475.Google Scholar
Yang, C., Grattoni, C. A., Muggeridge, A. H. & Zimmerman, R. M. 2000 A model for steady laminar flow through a deformable gel-coated channel. J. Colloid Interface Sci. 226, 105–111.Google Scholar
Zell, A., Gier, S., Rafai, S. & Wagner, C. 2010 Is there a relation between the relaxation time measured in caber experiments and the first normal stress coefficient? J. Non-Newtonain Fluid Mech. 165, 1265–1274.Google Scholar