Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T15:02:39.806Z Has data issue: false hasContentIssue false
  • English
  • Français

The effectiveness of an air curtain in the doorway of a ventilated building

Published online by Cambridge University Press:  01 September 2014

D. Frank  and
P. F. Linden
D. Frank*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
P. F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: D.Frank@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Air curtains are used to reduce the heat and mass exchange across open doorways. Their sealing ability is assessed in terms of the effectiveness 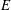$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$, the fraction of the exchange flow prevented by the air curtain compared to an unobstructed open door. Previous work has studied air-curtain effectiveness when the doorway is the only means of ventilating a space. In this paper, we examine the effects of additional displacement ventilation on the dynamics of the air curtain and the resulting changes in its effectiveness. The main controlling parameter is the deflection modulus 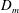$D_{m}$, which is the ratio between the momentum flux of the air curtain and the transverse forces due to the displacement ventilation. For a relatively warm interior, we find that, for small values of 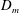$D_{m}$, the air curtain is drawn inside the space by the ventilation flow. For large values of 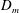$D_{m}$, the flow through the doorway is controlled by the air curtain. A smooth transition occurs between these two regimes, and we estimate the 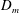$D_{m}$ value for the onset of this transition. Our model provides a quantitative prediction of 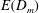$E(D_{m})$ in the ventilation-driven regime, and gives a qualitative description of the other two regimes. Laboratory experiments were conducted to test the proposed model. The experimental data were compared to theoretical predictions, and good agreement was found.

JFM classification

Convection: Convection in cavities Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 130 - 164
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beggs, C. B. 2003 The airborne transmission of infection in hospital buildings: fact or fiction? Indoor Built Environ. 12, 9–18.CrossRefGoogle Scholar
Brown, W. G. & Solvason, K. R. 1962 Natural convection through rectangular opening in partitions – Part I: vertical openings. Intl J. Heat Mass Transfer 5, 859–868.CrossRefGoogle Scholar
Chung, K. C. 1999 Three-dimensional analysis of airflow and contaminant particle transport in a partitioned enclosure. Build. Environ. 34, 7–17.CrossRefGoogle Scholar
Costa, J. J., Oliveira, L. A. & Silva, M. C. G. 2006 Energy savings by aerodynamic sealing with a downward-blowing plane air curtain – a numerical approach. Energy Build. 38, 1182–1193.CrossRefGoogle Scholar
Emswiler, J. 1926 The neutral zone in ventilation. J. Am. Soc. Heat. Vent. Engrs 32 (1), 1–16.Google Scholar
Etheridge, D. & Sandberg, M. 1996 Building Ventilation: Theory and Measurement. Wiley.Google Scholar
Foster, A. M. 2007 CFD optimization of air movement through doorways in refrigerated rooms. In Computational Fluid Dynamics in Food Processing (ed. Sun, D.-W.), Contemporary Food Engineering Series, pp. 167–194. CRC Press.CrossRefGoogle Scholar
Foster, A. M., Swain, M. J., Barrett, R., D’Agaro, P. D. & James, S. J. 2006 Effectiveness and optimum jet velocity for a plane jet air curtain used to restrict cold room infiltration. Intl J. Refrig. 29, 692–699.CrossRefGoogle Scholar
Foster, A. M., Swain, M. J., Barrett, R., D’Agaro, P. D., Ketteringham, L. P. & James, S. J. 2007 Three-dimensional effects of an air curtain used to restrict cold room infiltration. Appl. Math. Model. 31, 1109–1123.CrossRefGoogle Scholar
Fritzsche, C. & Lilienblum, W. 1968 Neue Messungen zur Bestimmung der Kälteverluste an Kühlraumtüren. Kältetechnik-Klimatisierung 20, 279–286.Google Scholar
Gonçalves, J. C., Costa, J. J., Figueiredo, A. R. & Lopes, A. M. G. 2012 CFD modelling of aerodynamic sealing by vertical and horizontal air curtains. Energy Build. 52, 153–160.CrossRefGoogle Scholar
Guyonnaud, L. & Solliec, C. 1998 Mass transfer analysis of an air curtain system. In Advances in Fluid Mechanics II (ed. Brebbia, C. A., Comini, G. & Rahman, M.), Engineering Sciences, vol. 18. WIT Press.Google Scholar
Guyonnaud, L., Solliec, C., de Virel, M. D. & Rey, C. 2000 Design of air curtains used for air confinement in tunnels. Exp. Fluids 28, 377–384.CrossRefGoogle Scholar
Hayes, F. C. & Stoecker, W. F. 1969a Heat transfer characteristics of the air curtain. Trans. ASHRAE 75 (2), 153–167.Google Scholar
Hayes, F. C. & Stoecker, W. F. 1969b Design data for air curtains. Trans. ASHRAE 75, 168–180.Google Scholar
Hoffman, P. N., Bennett, A. M. & Scott, G. M. 1999 Controlling airborne infections. J. Hosp. Infect. 43, 203–210.CrossRefGoogle ScholarPubMed
Howell, R. H. & Shibata, M. 1980 Optimum heat transfer through turbulent recirculated plane air curtains. Trans. ASHRAE 2567, 188–200.Google Scholar
Hunt, G. R. & Linden, P. F. 1999 The fluid mechanics of natural ventilation – displacement ventilation by buoyancy-driven flows assisted by wind. Build. Environ. 34, 707–720.CrossRefGoogle Scholar
Linden, P. F. 1999 The fluid mechanics of natural ventilation. Annu. Rev. Fluid Mech. 31, 201–238.CrossRefGoogle Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.CrossRefGoogle Scholar
Longdill, G. R., Frazerhurst, L. F. & Wyborn, L. G.1974 Air curtains. Tech Rep. 385. Meat Research Institute of New Zealand (MIRINZ).Google Scholar
Lu, F. K. & Fernandes, J. E.2008 Visualizing the flow induced by an air curtain over a mannequin using stereo particle image velocimetry. In Proceedings of the 13th International Symposium on Flow Visualization, 1–4 July 2008, Nice, France.Google Scholar
Maurel, S. & Solliec, C. 2001 A turbulent plane jet impinging nearby and far from a flat plate. Exp. Fluids 31, 687–696.CrossRefGoogle Scholar
Rajaratnam, N. 1976 Turbulent Jets. Elsevier Scientific.Google Scholar
Schlichting, H. 1955 Boundary Layer Theory. McGraw-Hill.Google Scholar
Sirén, K. 2003a Technical dimensioning of a vertically upwards blowing air curtain – part I. Energy Build. 35, 681–695.CrossRefGoogle Scholar
Sirén, K. 2003b Technical dimensioning of a vertically upwards blowing air curtain – part II. Energy Build. 35, 697–705.CrossRefGoogle Scholar
Tamm, W. 1966 Kälteverluste durch Kühlraumöffnungen. Kältetechnik-Klimatisierung 18, 142–144.Google Scholar
Wilson, D. J. & Kiel, D. E. 1990 Gravity driven counterflow through an open door in a sealed room. Build. Environ. 25 (4), 379–388.CrossRefGoogle Scholar

Movie 1

This movie shows the air curtain operating in the unstable regime. The left-hand side of the tank is filled with fluid of density ρland theright-hand side with fluid of density ρd. The flow through the top opening is unidirectional from light fluid half to dense fluid half of the tank. The intrusion current of dense fluid into the light fluid half of the tank along the bottom is visible. A plume of light fluid rises on the dense fluid side of the doorway. The plume origin is located slightly above the middle height of the doorway. The presence of this plume indicates that the air curtain is deflected to the dense fluid side, and that there is still bidirectional flow through the doorway

Download Movie 1(Audio)
Audio 4.6 MB

Movie 2

This movie shows the air curtain operating in the ventilation-driven regime. The left-hand side of the tank is filled with fluid of density ρl and the right-hand side with fluid of density ρd. The flow through the top opening is unidirectional from light fluid half to dense fluid half of the tank. The dense gravity current intrudes into the light-fluid side along the bottom of the tank. In this regime, no plume is observed on the dense fluid side of the doorway. This suggests that the air curtain is deflected completely to the light fluid side of the tank

Download Movie 2(Audio)
Audio 6.5 MB

Movie 3

This movie shows the air curtain operating in the transition regime. The left-hand side of the tank is filled with fluid of density ρl and the right-hand side with fluid of density ρd. The flow through the top opening is unidirectional from light fluid half to dense fluid half of the tank. The air curtain impinges on the tank bottom and there is a rising plume in the dense fluid half of the tank

Download Movie 3(Audio)
Audio 7.9 MB

Movie 4

This movie shows the air curtain operating in the air-curtain-driven regime. The left-hand side of the tank is filled with fluid of density ρl and the right-hand side with fluid of density ρd. The flow through the top opening is unidirectional from light fluid half to dense fluid half of the tank. The air curtain impinges on the bottom of the tank. Its flux divides equally between both sides of the tank after impingement on the bottom, so that a more pronounced plume than in the transition regime is visible in the dense fluid half of the tank

Download Movie 4(Audio)
Audio 7.9 MB