Effects of dilatation and turbulence on tangential strain rates in premixed hydrogen and iso-octane flames

Abstract

The tangential strain rate in premixed flames impacts significantly the flame surface area generation and thus the combustion process. Studies on incompressible isotropic turbulence have revealed that the mean tangential strain rate at material and iso-scalar surfaces is positive and exhibits a universal value when normalized by the Kolmogorov time. This is associated with the preferential alignment of the surface normal with the most compressive principal strain rate. The present study investigates such effects in premixed hydrogen and iso-octane flame kernels using direct numerical simulations. It is shown that the normalized mean tangential strain rate of the investigated flames has a very similar value compared with the incompressible flows. However, in the reaction zone, the flame surface normal aligns preferentially with the most extensive principal strain rate. Furthermore, this alignment depends on the reaction progress variable and the Lewis number, while the tangential strain rate remains independent of these parameters. Such counter-intuitive behaviour is systematically investigated by decomposing the effects of dilatation and residual solenoidal turbulence. It is found that the solenoidal turbulence influences significantly the tangential strain rate. A general effect of turbulence on the tangential strain rate is identified, which is consistent with incompressible flows and independent of the Lewis number and the reaction progress variable. This is a remarkable finding indicating that models of the tangential strain rate developed based on incompressible flows apply also to premixed flames with different Lewis numbers, and, for the modelling, only the solenoidal turbulence should be considered.

1. Introduction

For premixed flames, turbulence impacts the combustion process mainly through two mechanisms: (i) the flame surface area evolution and (ii) the local flame propagation speed (Bray 1990; Bray & Libby 1994; Peters 2001). The evolution of an element of flame surface area $\delta A$ can be described by the flame stretch rate

(1.1)\begin{equation} {K} = \frac{1}{\delta A} \frac{{\rm d} \delta A}{{\rm d} \tau}, \end{equation}

which can be written as follows (Candel & Poinsot 1990):

(1.2)\begin{equation} {K} = s_{d} \kappa + a_{t}. \end{equation}

It contains two components: $s_{d} \kappa$ accounts for the surface area change due to the flame propagation in the presence of curvature $\kappa$. Positive curvatures refer to convexly curved flame segments towards the unburned gas. The displacement speed, $s_{d}$, describes the relative motion of the flame surface to the flow field. The tangential strain rate, $a_{t}$, describes the influence of the flow on the evolution of the flame surface area and can be expressed as

(1.3)\begin{equation} a_{t} = \varDelta - \boldsymbol{n} \boldsymbol{n}: \boldsymbol{\nabla} \boldsymbol{u}, \end{equation}

where ${\varDelta =\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}}$ is the dilatation rate, $\boldsymbol {n}$ is the unit surface normal vector pointing towards the unburned gas and $\boldsymbol {u}$ is the flow velocity.

The impact of tangential strain rate on the evolution of material and propagating surfaces in incompressible flows and turbulent premixed flames has received considerable interest (Ashurst et al. 1987; Girimaji & Pope 1990; Yeung, Girimaji & Pope 1990; Girimaji & Pope 1992; Rutland & Trouvé 1993; Chakraborty & Swaminathan 2007; Kim & Pitsch 2007; Sankaran et al. 2007, 2015; Chakraborty, Klein & Swaminathan 2009; Hawkes et al. 2012; Dopazo et al. 2015; Wang, Hawkes & Chen 2016; Wang et al. 2017; Luca et al. 2019; Krisman et al. 2021; Kulkarni & Bisetti 2021; Berger, Attili & Pitsch 2022; Gauding et al. 2022). Yeung et al. (1990) investigated the straining of material surfaces in incompressible turbulence and found that the alignment of the surface normal with the principal strain rates plays a vital role for the average tangential strain rate at the surfaces. The tangential strain rate can be written as

(1.4)\begin{equation} a_{t} = \varDelta - \left( \lambda_1 \cos^2\varphi_1 + \lambda_2 \cos^2 \varphi_2 + \lambda_3 \cos^2\varphi_3 \right), \end{equation}

where $\lambda _i$ denotes the eigenvalues of the strain rate tensor ($\lambda _1 \geq \lambda _2 \geq \lambda _3$, $\lambda _1 + \lambda _2 + \lambda _3 = \varDelta$), and $\varphi _i$ is the angle between the surface normal and the principal strain rates, whose direction is given by the eigenvectors of the strain rate tensor. For incompressible flows,

(1.5a,b)\begin{equation} \varDelta = \lambda_1 + \lambda_2 + \lambda_3 = 0\quad \text{and} \quad \lambda_1> 0 > \lambda_3. \end{equation}

If the surface normal aligns with the most compressive principal strain rate,

(1.6a,b)\begin{equation} \cos^2 \varphi_1=\cos^2 \varphi_2=0\quad \text{and} \quad \cos^2 \varphi_3=1. \end{equation}

According to (1.4), a positive tangential strain rate is obtained: ${a_{t} = 0 - \lambda _3 > 0}$. Similarly, if the surface normal aligns with the most extensive principal strain rate, the tangential strain rate is negative: ${a_{t} = 0 - \lambda _1 < 0}$. Yeung et al. (1990) found that the normal of the material surface aligns preferentially with the most compressive principal strain rate, which results in a positive surface-averaged normalized tangential strain rate of $\tau _\eta \langle a_{t} \rangle _{s} = 0.28$, where $\tau _\eta$ is the Kolmogorov time. The operator $\langle {\cdot } \rangle _s$ denotes the surface average. It is worth noting that $a_{t}$ of a randomly oriented surface in incompressible isotropic turbulence has a zero mean. Girimaji & Pope (1990) and Gauding et al. (2022) demonstrated that the value $0.28$ holds valid in incompressible turbulence for a wide range of Reynolds and Schmidt numbers. In turbulent premixed flames, similar values of $\tau _\eta \langle a_{t} \rangle _{s}$ have been reported for various configurations by different authors using simplified Arrhenius one-step and detailed chemistry models, with and without the constant density assumption (Rutland & Trouvé 1993; Luca et al. 2019; Kulkarni & Bisetti 2021; Berger et al. 2022). However, Chakraborty et al. (2009) and Kim & Pitsch (2007) found that the flame surface normal can align preferentially with the most extensive principal strain rate in the reaction zone due to the dilatation from heat release. They did not evaluate the value of $\tau _\eta \langle a_{t} \rangle _{s}$, while Chakraborty et al. (2009) showed that the mean value of $a_{t}$ is positive. Therefore, it is not yet clear whether the specific value of $\tau _\eta \langle a_{t} \rangle _{s} \approx 0.28$ is also obtained for premixed flames when the flame surface normal aligns preferentially with the most extensive principal strain rate, and whether this varies for different combustion regimes. Further, the dependence of this alignment on the Lewis number and the value of the reaction progress variable used to define the flame surface appears to contradict the independence of the tangential strain rate on these parameters. Rutland & Trouvé (1993) found that $\tau _\eta \langle a_{t} \rangle _{s} =0.28$ holds for premixed flames with different Lewis numbers from $0.8$ to $1.2$. Dopazo et al. (2015) and Berger et al. (2022) showed that the averaged tangential strain rate is almost constant for different iso-surfaces of the reaction progress variable. Chakraborty et al. (2009) also reported that the distributions of the tangential strain rate are similar for different iso-surfaces of the reaction progress variable and different Lewis numbers ($0.34$ to $1.2$). However, they found that the alignment of the flame surface normal with the principal strain rates depends strongly on the Lewis numbers and the reaction progress variable.

The positive straining of material surfaces in incompressible flows ($\tau _\eta \langle a_{t} \rangle _{s} =0.28$) results from the preferential alignment of the surface normals with the most compressive principal strain rates (Yeung et al. 1990). Despite the differences in the alignment characteristics between flames and incompressible flows, coefficients and scaling law in the current models of the tangential strain rate on flame surfaces usually originate from studies on incompressible flows (Cant, Pope & Bray 1991; Duclos, Veynante & Poinsot 1993; Hawkes & Cant 2001; Chakraborty 2021) with Reynolds-averaged quantities replaced by Favre-averaged quantities. A particular example is the flame surface density (FSD) approach, where the sub-grid tangential strain rate in the transport equation of FSD is often modelled by using the Kolmogorov time scale as $0.28(\tilde {\epsilon }/\nu _0)^{1/2}$, where $\tilde {\epsilon }$ is the Favre-averaged dissipation rate and $\nu _0$ is the unburned-gas kinematic viscosity (Cant et al. 1991; Chakraborty 2021). A better understanding of the effects of heat release, dilatation, and their interactions with turbulence on the tangential strain rate and the alignment of the flame surface normal with the principal strain rates in premixed flames will shed more light on the modelling of turbulent premixed combustion. The first objective of the current work is to investigate these effects by introducing a decomposition approach to separately consider the effects of combustion, namely dilatation, and the residual solenoidal turbulence in premixed flames. It is hypothesized that the solenoidal part of the turbulence in premixed flames governs the tangential strain rate and has the same effects as in incompressible flows.

The second objective of the current work is to assess the local effects of the small-scale turbulence on the local tangential strain rate, which is of importance for the early development of flame kernels in spark-ignition (SI) internal combustion engines (ICEs) (Chu et al. 2023a). The variations of such early flame kernel development influence significantly the cycle-to-cycle variations (CCVs) in SI ICEs (Young 1981; Schiffmann, Reuss & Sick 2018; Zeng et al. 2019; Chu et al. 2022), and thus are of practical importance for the design and optimization of such engines (Aleiferis et al. 2004; Fontana & Galloni 2010; Jung, Sasaki & Iida 2017; Karvountzis-Kontakiotis et al. 2017; Luszcz et al. 2018; Kargul et al. 2019; Ye et al. 2021). In an SI ICE, the initial flame kernel ignited by a spark is typically smaller than the size of the turbulent integral length scales (Falkenstein et al. 2020a). The evolution of such small flame kernels is dominated by local, intermittent flow fluctuations, which are not well represented by their ensemble average and thus can vary under the same nominal conditions. Therefore, it is of practical interest to assess the effects of the local small-scale turbulence on the local tangential strain rate.

For these purposes, the DNS database (Chu et al. 2023a) of hydrogen and iso-octane flame kernels under engine conditions with significantly different Lewis numbers and turbulence-flame interactions is analysed. The paper is organized in the following manner. First, a brief description of the DNS database is provided. Then, the analysis results are presented and discussed, including an approach for separating the effects of solenoidal turbulence and dilatation on the tangential strain rate in premixed flames. Finally, the paper finishes with conclusions.

2. DNS database

2.1. Configuration

In this study, the DNS database by Chu et al. (2023a) and Falkenstein et al. (2020a) consisting of multiple realizations of premixed hydrogen and iso-octane flame kernels under engine conditions with significantly different Lewis numbers is considered. The flame kernels were ignited in a decaying homogeneous isotropic turbulent (HIT) field of homogeneous fuel–air mixtures. The HIT field is initialized using the same method as Kulkarni et al. (2021). The thermodynamic parameters were specified to represent part load operation conditions of gasoline SI engines (Falkenstein et al. 2020a) and medium load conditions of hydrogen engines (Tang et al. 2002; Verhelst et al. 2009; Jilakara et al. 2015). The volumetric energy density ratio of the hydrogen mixture to the iso-octane mixture is approximately 2 : 1. The flow parameters, such as turbulent Reynolds number $Re_{t}$, Karlovitz number $Ka$ and Damköhler number $Da$, were specified as closely as possible to typical SI engine conditions, which can be found from Falkenstein et al. (2020a). The characteristic numbers of the DNS are listed in table 1. Flames for both fuels fall into the thin reaction zones regime of premixed turbulent combustion. Multiple realizations of turbulent flame kernels were simulated for both fuels by placing the ignition source at different locations in the same initial turbulent flow field. Ignition was realized by a heat source varying smoothly in time and space as used by Falkenstein et al. (2020a). The ignition energy was specified as 1.4 times the minimum ignition energy, which was determined in a quiescent environment and different in the two mixtures, to ensure successful ignition in the turbulent fields (Falkenstein et al. 2020a; Chu et al. 2023b). For a detailed description of the DNS database including the specification of the ignition locations for different realizations, the readers are referred to Chu et al. (2023a). In this study, the fastest and the slowest flame kernels for each fuel are considered, which exhibit significantly different kernel growth rates and tangential strain rates. It is worth noting that in this study, the configuration of developing flame kernels is considered because the tangential strain rate of very early flame kernels has tremendous practical interest as it was found to significantly influence the growth rate of the kernels (Chu et al. 2023a), which has leading order effect on the cycle-to-cycle variations of SI engines. The main findings discussed in this study remain unchanged when a planar turbulent flame is considered, which is shown in Appendix B.

Table 1. Conditions and characteristic numbers of DNS: turbulent Reynolds number ${\textit {Re}_{t}=l_{t} u'/\nu }$, root mean square of the turbulent velocity fluctuations $u'$, turbulent integral length scale ${l_{t} = u'^3 / \bar {\epsilon }}$, mean dissipation rate $\bar {\epsilon }$, kinematic viscosity ${\nu }$, Reynolds number based on Taylor length scale ${\textit {Re}_\lambda =l_\lambda u'/\nu }$, Taylor length scale ${l_\lambda = ( 15 \nu u'^2 / \bar {\epsilon } )^{1/2}}$, unstretched laminar flame speed $s_{l}^{0}$, Karlovitz number $Ka=\tau ^0_{f}/\tau _{\eta }$, Damköhler number $Da=\tau _{t}/\tau ^0_{f}$, chemical time $\tau ^0_{f}=l_{f}^{0}/s_{l}^{0}$, Kolmogorov time $\tau _\eta = ( \nu / \bar {\epsilon } )^{1/2}$, turbulent integral time $\tau _{t}=l_{t}/ u'$, unstretched laminar flame thickness computed from the maximum temperature gradient $l_{f}^{0}$, Kolmogorov length $l_\eta$, cell size $\Delta x$, initial pressure $p$ and temperature $T_{u}$, fuel/air equivalence ratio $\phi$, effective Lewis number evaluated according to Joulin & Mitani (1981) $Le_{eff}$, and ignition radius $R_{ign}$.

2.2. Governing equations and numerical methods

The reacting flow has been modelled in the low-Mach limit (Müller 1998), and chemical reactions have been described for hydrogen and iso-octane combustion with a detailed mechanism proposed by Konnov (2019) and a modified model (Falkenstein et al. 2020a) based on the skeletal iso-octane mechanism by Pitsch, Peters & Seshadri (1996), respectively. The two mechanisms have been validated with experiments under different conditions. The diffusive scalar transport has been modelled with the Curtiss–Hirschfelder approximation (Hirschfelder et al. 1964). The diffusion coefficients have been determined by setting the species Lewis numbers constant and computing them in the burned gas of the corresponding unstretched laminar flames. The Soret effect has been included following Zhou et al. (2017) and Schlup & Blanquart (2018) with a mixture-averaged thermal diffusion model. The ideal gas law has been applied as the equation of state. The DNS has been carried out with a semi-implicit finite difference code based on the Crank–Nicolson time advancement scheme and an iterative predictor-corrector scheme with spatial and temporal staggering (Desjardins et al. 2008). The Poisson equation for the pressure correction has been solved by the multi-grid HYPRE solver (Falgout & Yang 2002). Second-order central difference schemes have been employed for momentum convection and all diffusive fluxes, while a fifth-order weighted essentially non-oscillatory (WENO) (Jiang & Shu 1996) scheme has been applied for scalar convection to ensure bounded solutions. For species and temperature, the operator splitting proposed by Strang (1968) has been used. The resulting ordinary differential equation for chemical source terms has been solved using the CVODE solver from the SUNDIALS package (Hindmarsh et al. 2005).

3. Results and discussion

To analyse premixed flames, it is useful to define a reaction progress variable. In this study, the reaction progress variable $C$ of the hydrogen flame kernels is defined using the mass fraction of molecular hydrogen $Y_{\mathrm {H}_2}$, as suggested by Berger et al. (2022),

(3.1)\begin{equation} C=1-Y_{\mathrm{H}_2}/Y_{\mathrm{H}_{2,{u}}},\end{equation}

where $Y_{\mathrm {H}_{2,{u}}}$ is the hydrogen mass fraction in the unburned gas mixture. For the iso-octane flame kernels, as in the studies by Falkenstein et al. (2020b) and Chu et al. (2023a), a reaction progress variable $C$ is defined by the solution of the transport equation

(3.2)\begin{equation} \rho\frac{\partial C }{\partial \tau}+ \rho \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} C =\dot{\omega}'''_{C} + \boldsymbol{\nabla} \boldsymbol{\cdot} \left(\rho D_{th} \boldsymbol{\nabla} C\right), \end{equation}

where $D_{th}=\lambda / (\rho c_p)$ denotes the thermal diffusivity, $\lambda$ the thermal conductivity, $\rho$ the density and $c_{p}$ the specific heat capacity. The chemical source term $\dot {\omega }'''_C$ is defined based on the major product species,

(3.3)\begin{equation} \dot{\omega}'''_C = \dot{\omega}'''_{\mathrm{H}_\mathrm{2}}+ \dot{\omega}'''_{\mathrm{H}_\mathrm{2}\mathrm{O}} + \dot{\omega}'''_\mathrm{CO}+ \dot{\omega}'''_{\mathrm{CO}_\mathrm{2}}. \end{equation}

Equation (3.2) exhibits a simplified diffusion term without differential diffusion. In the DNS, the passive scalar $C$ is solved solely for post-processing, which does not influence the simulation results, however, simplifies significantly the analysis of premixed flames (Falkenstein et al. 2020b). Falkenstein et al. (2020b) have shown that this simplification has negligible influence under the investigated conditions. This progress variable definition is used so that the analysis in this study is consistent with our previous studies (Falkenstein et al. 2020b; Chu et al. 2023a). Using other progress variable definitions, such as $C=Y_{\mathrm {CO}_2}$, does not change the main findings in this study. Results using $C=Y_{\mathrm {CO}_2}$ are provided in Appendix B. The flame surface can be defined as an iso-surface of $C$. The surface average of a quantity $Q$ on the surface of $C=C_0$ is given as

(3.4)\begin{equation} \langle Q \rangle_{{s},C_0} = \frac{\displaystyle\int Q \left|\boldsymbol{\nabla} C \right| \delta \left( C - C_0 \right){\rm d}V }{\displaystyle\int \left|\boldsymbol{\nabla} C \right| \delta \left( C - C_0 \right) {\rm d}V},\end{equation}

where $\delta$ is the Dirac delta function. In premixed combustion, quantities may vary for different iso-surfaces of $C$. The average behaviour of a quantity $Q$ considering all iso-surfaces of $C$ can be described by the generalized iso-surface average (Boger et al. 1998), which is given by

(3.5)\begin{equation} \langle Q \rangle = \frac{\displaystyle\int Q \left|\boldsymbol{\nabla} C \right| {\rm d}V }{\displaystyle\int\left|\boldsymbol{\nabla} C \right| {\rm d}V}.\end{equation}

In this study, two flame kernel realizations are considered for each fuel. Figure 1 shows the evolution of the fuel consumption rate, which is expressed as the normalized integrated reaction progress variable source term, $\dot {\varOmega }^*_C= \int \dot {\omega }_C \,{\rm d}V /(\rho _u s^0_{l} A_{ref} C_{max})$. Here, $A_{ref}=4{\rm \pi} R_{ign}$ is a normalization constant. Significant differences in the fuel consumption rate between the two realizations are observed for each fuel. Realizations that exhibit the larger (or smaller) fuel consumption rate are referred to as ‘fast’ (or ‘slow’) kernels. Such difference in the fuel consumption rate for each fuel is attributed to the various tangential strain rates of different realizations, which are shown in figure 2. A comprehensive discussion of the impact of tangential strain rate on the fuel consumption rate can be found from Chu et al. (2023a). In figure 2, the generalized iso-surface average of the tangential strain rate is presented, as it directly influences the fuel consumption rate (Chu et al. 2023a). Quantities are normalized by the chemical time ${\tau ^0_{f}= l^0_{f} / s^0_{l}}$, which is the same for the fast and slow kernels of each fuel (table 1). The initial high values are due to ignition. Different realizations of both fuels exhibit substantial variations in tangential strain rates shortly after ignition. This originates from the different flow conditions around the ignition locations. A trend towards the same value is observed in both fuels as the kernels grow since the homogeneous statistical behaviour of the flame-turbulence interactions in HIT is expected for spherical flames of sizes much larger than the turbulent integral length scale. In the following, the tangential strain rates of both fuels at various times are examined. Specifically, the analysis will focus on time instances at $\tau =0.5\tau ^0_{f}$ for both fuels with large $a_{t}$ differences between the fast and the slow flame kernels, as well as $\tau =2\tau ^0_{f}$ for hydrogen and $\tau =4\tau ^0_{f}$ for iso-octane with small differences of $a_{t}$. An illustration of the selected eight cases is provided in figure 3. Significant differences among the cases can be identified, for example, the flame kernel topology, the surface wrinkling, the size of the flame kernels compared with the turbulent integral length, and the distribution of the heat release rate in positively and negatively curved regions. Such database makes possible a direct test of the proposed hypothesis. A general behaviour of the tangential strain rate and the alignment of the strain rate tensor with the surface is hypothesized for all the cases after decomposition. For a detailed comparison of the different cases and the explanation for the difference, the readers are referred to our previous studies (Chu et al. 2023a, 2023b).

Figure 1. Normalized integrated reaction progress variable source term as a function of normalized time (Chu et al. 2023a): (a) hydrogen and (b) iso-octane.

Figure 2. Generalized iso-surface average of the tangential strain rate as a function of time (Chu et al. 2023a). The variables are normalized with the chemical time $\tau ^0_{f}$. (a) Hydrogen and (b) iso-octane.

Figure 3. Illustration of the selected eight cases: iso-surface of progress variable corresponding to maximum heat release (in an unstretched flame) coloured with heat release rate (Chu et al. 2023a). For the sake of comparability, the size of the kernels is rescaled so that the turbulent integral length $l_{t}$ for both fuels has the same length in the figure, which is displayed on the top right.

3.1. Tangential strain rate and dilatation rate

Figure 4 shows the surface averaged tangential strain rate $\langle a_{t} \rangle _{{s},C}$ and dilatation rate $\langle \varDelta \rangle _{{s},C}$ as functions of the reaction progress variable $C$. The tangential strain rate has been normalized with the Kolmogorov time evaluated in the unburned mixture ($C \approx 0.01$), ${\tau _\eta =(\nu /\bar {\epsilon })^{1/2}}$, using the average dissipation rate in the unburned mixture, $\bar {\epsilon }$. It is worth noting that $\tau _\eta$ is different for different cases. In particular, for each fuel at $0.5\tau ^0_{f}$, $\tau _\eta$ of the fast and the slow kernels are significantly different. The dilatation rate has been normalized with both the Kolmogorov time ${\tau _\eta }$ and the chemical time $\tau ^0_{f}$ which is a constant for each fuel. As a reference, the joint probability density functions (j.p.d.f.s) for the fast kernel at the later time, $2\tau ^0_{f}$ for hydrogen and $4\tau ^0_{f}$ for iso-octane, are also displayed. As expected, the flame heat release causes positive dilatation rates in the reaction zone. At $0.5\tau ^0_{f}$, the ignition heat source is still affecting the flame as shown by the increased normalized dilatation rate $\tau ^0_{f} \varDelta$ compared with the later time for both fuels. The dilatation rate normalized with the Kolmogorov time ${\tau _\eta \varDelta }$ describes its relative strength compared with small-scale turbulence, which is different for fast and slow kernels. In contrast to the dependence of the dilatation rate on the progress variable, the tangential strain rate is almost constant across the flame for both fuels, which is consistent with the results of Dopazo et al. (2015) and Berger et al. (2022). Even though the value of the absolute tangential strain rate at $0.5\tau ^0_{f}$ of the fast kernel is approximately twice as large as the slow kernel for both fuels (figure 2) and the flames at $0.5\tau ^0_{f}$ exhibit stronger dilatation rates due to the ignition heat source, the tangential strain rate normalized with the Kolmogorov time scale is almost the same and close to the value of $\tau _\eta \langle a_{t} \rangle _{s} \approx 0.28$ for all cases. Similar values of $\tau _\eta \langle a_{t} \rangle _{s}$ have also been reported by different authors for various configurations and fuels: planar premixed flames in HIT with single-step Arrhenius kinetics chemistry and constant density by Rutland & Trouvé (1993), premixed methane–air jet flames with detailed chemistry by Luca et al. (2019), spherically expanding premixed methane–air flames in HIT with detailed chemistry by Kulkarni & Bisetti (2021), and premixed hydrogen–air jet flame with detailed chemistry by Berger et al. (2022). Moreover, Kulkarni & Bisetti (2021) demonstrated that the normalized tangential strain rate is independent of the Reynolds number in the range of $Re_\lambda = 44\unicode{x2013}77$ and the Karlovitz number in the range of $Ka=25\unicode{x2013}59$. It is worth noting that this value is also in very good agreement with the study by Yeung et al. (1990), who investigated the strained material surfaces in incompressible isotropic turbulence. The reason why the tangential strain rate of premixed flames has the same value as material surfaces in incompressible flows and under which conditions this holds valid are discussed in the following sections.

Figure 4. Normalized tangential strain rate $\tau _\eta \langle a_{t} \rangle$, and dilatation rate $\tau ^0_{f} \langle \varDelta \rangle$ and $\tau _\eta \langle \varDelta \rangle$ as functions of $C$. The variables are normalized with the chemical time $\tau ^0_{f}$ or the Kolmogorov time, $\tau _\eta$, evaluated in the unburned mixture. (a,c,e) Hydrogen and (b,d,f) iso-octane. The colour maps represent the j.p.d.f. of the fast kernels at $2\tau ^0_{f}$ for hydrogen and $4\tau ^0_{f}$ for iso-octane.

3.2. Alignment of the flame normal with the principal strain rates

The value of $\tau _\eta \langle a_{t} \rangle _{s} \approx 0.28$ for material surfaces in incompressible flows results from the persistent straining of the surfaces due to the preferential alignment of the surface normal with the most compressive principal strain rates. In this section, such alignment characteristics in the premixed hydrogen and iso-octane flame kernels are assessed. Figure 5 shows the surface averaged alignment characteristics of the strain rate tensor and the normal vector of the iso-surfaces of $C$ as functions of $C$. The strain rate tensor and the normal vector are computed independently for each iso-surface of $C$. The alignment characteristics are expressed by the term $\cos \varphi _i$ (cf. (1.4)) with ${\cos ^2 \varphi _1+ \cos ^2 \varphi _2+ \cos ^2 \varphi _3=1}$. The probability density functions (p.d.f.s) of $\cos \varphi _i$ for the fast kernels at the later time, $2\tau ^0_{f}$ for hydrogen and $4\tau ^0_{f}$ for iso-octane, are provided in Appendix A (figure 18). Here, $\cos \varphi _i$ varies across the flame and exhibits different behaviours for different cases (cf. the surface average in figure 5). This is consistent with the previous findings by Chakraborty et al. (2009), who showed that the alignment characteristics of the flame surface normal with the principal strain rates are significantly influenced by the Lewis number and the value of the reaction progress variable used to define the flame surface. The dependence of the alignment characteristics on the reaction progress variable was also reported by Kim & Pitsch (2007). According to figures 4 and 5, it can be concluded that for regions with low dilatation rates, the normals of the iso-surfaces of $C$ align preferentially with the most compressive principal strain rates (${\cos \varphi _3 \to 1}$), such as $C<0.3$ for the hydrogen flames and $C$ close to $0$ for the iso-octane flames. Differences in the alignment characteristics between the hydrogen and the iso-octane flames are consistent with the differences in the dilation rates, $\tau _\eta \varDelta$, as shown in figure 4. The alignment with the most compressive principal strain rates indicates that turbulence presses the iso-surfaces together and increases the gradients of the scalar fields. This is consistent with the iso-surfaces of passive mixing scalars in turbulent flows (Kerr 1985; Ashurst et al. 1987; Warhaft 2000). However, for regions with high dilatation rates, the surface normals align preferentially with the most extensive principal strain rates (${\cos \varphi _1 \to 1}$), such as $C=0.7$ for the hydrogen flames and $C=0.4$ for the iso-octane flames. This is attributed to the fact that the dilatation due to combustion strongly accelerates the flow in the flame normal direction resulting in extensive strain rates in this direction, which indicates that the dilatation pushes the iso-surfaces away from each other and decreases the scalar gradient. This competing effect of turbulence and dilatation determines the alignment of the principal strain rates in premixed flames. Similar effects of dilatation on the alignment characteristics have also been found and discussed in previous studies (Swaminathan & Grout 2006; Chakraborty & Swaminathan 2007; Kim & Pitsch 2007; Wang et al. 2016, 2017). For flames with sufficiently high Karlovitz numbers, where the turbulent strain rates are dominant over the flame-induced dilatation, the flame normals tend to align with the most compressive principal strain rates even in reaction zones (Hamlington, Poludnenko & Oran 2011; Wang et al. 2016, 2017). In addition, Wang et al. (2016, 2017) have demonstrated that these alignment statistics can significantly depend on the axial distance in jet flames. In the upstream region close to the nozzle exit, where the flame remains laminar-like, there is no preferential alignment between the flame normal and the most compressive or extensive principal strain rates. However, how this impacts the tangential strain rate, which is a key factor for flame–turbulence interactions and the flame surface wrinkling, is not yet fully understood because, considering the importance of the alignment characteristics for the tangential strain rate, the dependence of the alignment characteristics on the reaction progress variable and the Lewis number appear to contradict the independence of the tangential strain rate on these parameters. The same mean tangential strain rate in regions with and without dilation implies a general effect of turbulence on the tangential strain rate, which is not influenced by dilatation and the alignment of the principal strain rates.

Figure 5. Alignment characteristics between the principal strain rates and the iso-surfaces of $C$, expressed by $\cos \varphi _i$, as a function of $C$. Symbols represent the conditional surface average for different cases as given in figure 4. (a,c,e) Hydrogen and (b,d,f) iso-octane.

3.3. Decomposition of the impact of dilatation and solenoidal turbulence

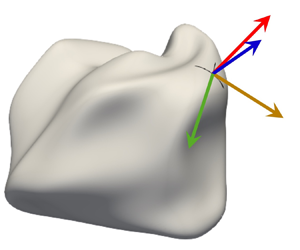
Inspired by the constant scaling of the tangential strain rate with the Kolmogorov time scale observed in figure 4 and incompressible flows (Girimaji & Pope 1990; Yeung et al. 1990; Gauding et al. 2022), it is hypothesized that small-scale turbulence governs the tangential strain rate in premixed flames in the same way as in incompressible flows, despite the presence of dilatation. To test this hypothesis, the effects of dilatation and the residual solenoidal turbulence, which features zero divergence, are examined separately. The separate treatment of solenoidal and dilatational parts of turbulent flows has been applied in various studies on compressible flows (Wang et al. 2018; Panickacheril John, Donzis & Sreenivasan 2021; Zheng et al. 2021, 2022; Sabelnikov et al. 2023) using the Helmholtz decomposition (Helmholtz 1858). In this study, an approach similar to the Helmholtz decomposition is proposed to separate the solenoidal and dilatational contributions in the velocity gradient tensor in the context of premixed flames. The main idea behind the separation approach is that the local flow caused by flame dilatation is mainly in the direction of the flame surface normal and does not change significantly in the directions tangential to the surface. For the derivation, it is convenient to introduce a local curvilinear coordinate system $(\eta, t, b)$ attached to the flame surface, as also applied by Thiesset et al. (2017), since the effects of dilatation depend on the normal direction and the topology of the flame surface. Here, $\eta$ is the distance to the surface along the normal, and $b$ and $t$ are the curvilinear coordinates on the flame surface aligned with the principal directions of curvature at each point of the surface as shown in figure 6. This coordinate system is also referred to as the Darboux frame in differential geometry (Prautzsch & Boehm 2018). The corresponding base vectors in the normal, tangential and binormal directions are denoted by $\boldsymbol{e}_\eta$, $\boldsymbol {e}_t$ and $\boldsymbol {e}_b$, respectively. Here, $\boldsymbol {e}_t$ and $\boldsymbol {e}_b$ are the directions of the principal curvatures $\kappa _1$ and $\kappa _2$ with $\kappa _1 > \kappa _2$. The directions are specified such that $\boldsymbol {e}_\eta$ points in the direction of the unburned gas and $\boldsymbol {e}_b= \boldsymbol {e}_t \times \boldsymbol {e}_\eta$.

Figure 6. The flame Darboux frame.

The velocity gradient tensor, $\boldsymbol {\nabla } \boldsymbol {u}$, is decomposed into two parts:

(3.6)\begin{equation} \boldsymbol{\nabla} \boldsymbol{u} = \boldsymbol{\nabla} \boldsymbol{u}_{s} + \boldsymbol{\nabla} \boldsymbol{u}_{d},\end{equation}

where $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ and $\boldsymbol {\nabla } \boldsymbol {u}_{d}$ denote the contributions from solenoidal turbulence and dilatation, respectively, so that

(3.7a,b)\begin{equation} \varDelta = \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u} = \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}_{d} \quad \mathrm{and} \quad \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}_{s} = 0. \end{equation}

In the following, $\boldsymbol {\nabla } \boldsymbol {u}_{d}$ in the flame Darboux frame is derived. The flame Darboux frame simplifies the derivation since $\boldsymbol {\nabla } \boldsymbol {u}_{d}$ depends on the normal direction and the topology of the flame surface. Assume that the local flow caused by flame dilatation is only in the direction of the normal vector and does not change strongly in the directions tangential to the surface:

(3.8)\begin{equation} \left.\begin{gathered} u_{{d},t} = u_{{d},b} = 0,\\ \frac{\partial u_{{d},\eta}}{ \partial t} = \frac{\partial u_{{d},\eta}}{\partial b} = 0, \end{gathered}\right\} \end{equation}

where $u_{{d},t}$, $u_{{d},b}$ and $u_{{d},\eta }$ are the components of $\boldsymbol {u}_{d}$ in the direction of $\boldsymbol {e}_t$, $\boldsymbol {e}_b$ and $\boldsymbol {e}_\eta$, respectively. It is worth noting that such assumptions may be invalid in flame surface regions with high curvatures. However, as will be shown in figure 9, for the investigated flames in the thin reaction zones regime, the main fraction of the flame surface (${\geq }85\,\%$) exhibits small curvatures compared with the reciprocal of the flame thickness. The velocity gradient $\boldsymbol {\nabla } \boldsymbol {u}_{d}$ is then simplified as

(3.9)\begin{equation} \boldsymbol{\nabla} \boldsymbol{u}_{d} = \frac{\partial u_{{d},\eta}}{\partial \eta} \boldsymbol{e}_\eta \boldsymbol{e}_\eta +\kappa_1 u_{{d},\eta} \boldsymbol{e}_t \boldsymbol{e}_t +\kappa_2 u_{{d},\eta} \boldsymbol{e}_b \boldsymbol{e}_b, \end{equation}

where only components on the diagonal are present. For a given flame surface, $\boldsymbol {e}_\eta$, $\boldsymbol {e}_t$, $\boldsymbol {e}_b$, $\kappa _1$ and $\kappa _2$ in (3.9) are known; however, $\partial u_{{d},\eta }/\partial \eta$ and $u_{{d},\eta }$ are unknown and determined by the following procedure. The dilatation rate is known and given by

(3.10)\begin{equation} \varDelta = \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}_{d} = \frac{\partial u_{{d},\eta}}{\partial \eta} + \kappa_1 u_{{d},\eta} + \kappa_2 u_{{d},\eta}. \end{equation}

There is only one equation (3.10) available for two unknown variables $\partial u_{{d},\eta }/\partial \eta$ and $u_{{d},\eta }$, so another relation is needed. Figure 7 illustrates schematically the local dilatation-induced velocity, where ${r = 1 / \kappa }$ is the radius of curvature $\kappa$. For small curvature with ${r \gg l_{f}}$, ${\kappa u_{{d},\eta } = u_{{d},\eta } / r}$ is negligible compared with $\partial u_{{d},\eta }/\partial \eta$. For large curvature, it applies ${\kappa u_{{d},\eta } = u_{{d},\eta }/r \approx \partial u_{{d},\eta } /\partial \eta }$. Therefore, a relation between ${\partial u_{{d},\eta }}/{\partial \eta }$ and $\kappa _1 u_{{d},\eta }$ or $\kappa _2 u_{{d},\eta }$ can be determined based on the flame thickness, $l_{f}$, and the principal curvature with the larger magnitude, $\kappa _{m}$. It is assumed that

(3.11)\begin{equation} \begin{cases} \kappa_{1} u_{{d},\eta} = \kappa_{2} u_{{d},\eta} = 0 & \text{if}\ \left| \kappa_{m} \right| < 1/l_{f} \\[10pt] \kappa_{m} u_{{d},\eta} =\dfrac{\partial u_{{d},\eta}}{\partial \eta},\ \kappa_{n} u_{{d},\eta} = \dfrac{ \kappa_{n} }{ \kappa_{m}} \dfrac{\partial u_{{d},\eta}}{ \partial \eta} & \text{otherwise}, \end{cases}\end{equation}

where

(3.12)\begin{equation} \begin{cases} m = 1, n = 2 & \text{if}\ \left| \kappa_1 \right| > \left| \kappa_2 \right|\\ m = 2, n = 1 & \text{otherwise}. \end{cases}\end{equation}

Here, $\kappa _1$ and $\kappa _2$ can be positive or negative. Additionally, $l_{f}$ is influenced by flame interactions with turbulence and thermodiffusive instabilities, and thus can be different from the thickness of the corresponding unstretched laminar flames. In this study, $l_{f}$ for the turbulent flames is computed from the maximum conditional mean of the reaction progress variable gradient conditioned on the reaction progress variable, $\textrm {max} \{ \overline { \boldsymbol {\nabla }C _C } \}$, where $C$ is the reaction progress variable. According to (3.9), (3.10), (3.11) and (3.12), $\boldsymbol {\nabla } \boldsymbol {u}_{d}$ in the global coordinate system can be expressed as in (3.13). The effects of solenoidal turbulence on the tangential strain rate can be evaluated by only considering the contributions of $\boldsymbol {\nabla } \boldsymbol {u}_{s}$, which can be obtained by (3.6) and (3.13).

(3.13)\begin{equation} \boldsymbol{\nabla} u_{{d},ij} = \begin{cases} \varDelta \boldsymbol{e}_{\eta,i} \boldsymbol{e}_{\eta,j} & \text{if}\ \left| \kappa_{1} \right|, \left| \kappa_{2} \right| < \dfrac{1}{ l_{f} },\\[10pt] \dfrac{\varDelta}{2 + \kappa_2/\kappa_1} \boldsymbol{e}_{\eta,i} \boldsymbol{e}_{\eta,j} +\dfrac{\varDelta}{2 + \kappa_2/\kappa_1} \boldsymbol{e}_{t,i} \boldsymbol{e}_{t,j} +\dfrac{\varDelta\kappa_2/\kappa_1}{2 + \kappa_2/\kappa_1} \boldsymbol{e}_{b,i} \boldsymbol{e}_{b,j} & \text{if}\ \left| \kappa_{1} \right| > \dfrac{1}{ l_{f} }\\ & \quad \text{and}\ \left| \kappa_{1} \right| > \left| \kappa_{2} \right|, \\[10pt] \dfrac{\varDelta}{2 + \kappa_1/\kappa_2} \boldsymbol{e}_{\eta,i} \boldsymbol{e}_{\eta,j} +\dfrac{\varDelta\kappa_1/\kappa_2}{2 + \kappa_1/\kappa_2} \boldsymbol{e}_{t,i} \boldsymbol{e}_{t,j} +\dfrac{\varDelta}{2 + \kappa_1/\kappa_2} \boldsymbol{e}_{b,i} \boldsymbol{e}_{b,j} & \text{if}\ \left| \kappa_{2} \right| > \dfrac{1}{ l_{f} }\\ & \quad \text{and}\ \left| \kappa_{2} \right| > \left| \kappa_{1} \right|. \end{cases}\end{equation}

Figure 7. Schematic of local dilatation-induced velocity.

Contributions of dilatation on the tangential strain rate expressed as $\langle a_{t} - a^+_{t} \rangle$ are shown in figure 8. Quantities evaluated with $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ are denoted by the superscript ‘$+$’. For most of the flame regions, the tangential strain rate is not influenced significantly by dilatation, which is illustrated by the almost zero value of $\langle a_{t} - a^+_{t} \rangle$. This is consistent with figure 4 and demonstrates that for most of the flame surface, dilation only influences the velocity gradient in the direction of the flame normal. According to (3.13), this corresponds to the surface segments with ${| \kappa _{1} |, | \kappa _{2} | < 1/ l_{f}}$. As shown in figure 9, most of the flame surface (${>}80\,\%$) is under this condition. Note that for highly curved flame segments, dilatation affects also the velocity gradient tangential to the flame surface.

Figure 8. Effects of dilatation on the normalized tangential strain rate $\tau _\eta a_{t}$. The superscript $+$ denotes a quantity evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6). Symbols represent the conditional surface average for different cases as given in figure 4. (a) Hydrogen and (b) iso-octane. For the sake of comparability, the range of the $y$-axis is kept the same as the tangential strain rate in figure 4.

Figure 9. Percentage of surface with $| \kappa _{1} |, | \kappa _{2} | < 1/ l_{f}$.

3.4. Alignment of the flame normal with the principal strain rates evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$

In this section, the alignment characteristics of the principal strain rates of the solenoidal turbulence evaluated with the decomposed velocity gradient, $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6), are analysed. As shown in figure 10, surface normals align preferentially with the most compressive principal strain rates across the entire flame for all eight cases, which is almost independent of $C$ and consistent with the alignment characteristics for material surfaces in incompressible flows. This indicates that even in regions with high dilatation, the residual solenoidal turbulence has the same effect as in regions without dilatation. It orients the flame surface such that the surface normals align with the most compressive principal strain rates of the solenoidal turbulence. It is remarkable that even though the flame interactions with turbulence and thus the flame kernel topology are significantly different between the hydrogen and iso-octane flame kernels and different realizations of each fuel (cf. figure 3), the local flame surface direction is always determined by the solenoidal turbulence independent of the Lewis number and the location of the surface in the flame. In addition, even at $0.5\tau ^0_{f}$, which is shortly after ignition with substantial ignition effects and not much flame surface wrinkling has been developed, especially for the slow kernels, the same behaviour is obtained. This is consistent with Girimaji & Pope (1992), who showed that the preferential alignment of initially randomly oriented surface elements with the principal strain rates is obtained after an initial transient period of a few Kolmogorov time scales, which indicates that the surface reorientation is a small-scale phenomenon. The fact that the general behaviour also applies to the very early phase in the flame kernel development is of vital importance for the modelling of flame kernels since the kernel growth rates correlate significantly to the tangential strain rate at $0.5\tau ^0_{f}$ in the investigated DNS (Chu et al. 2023a). An illustration of the directions of the local instantaneous principal strain rates evaluated using $\boldsymbol {\nabla } \boldsymbol {u}$ and $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ is given in figure 11. The dilatation changes the directions of the principal strain rates. The surface normal aligns with the most extensive principal strain rate, $e_1$, evaluated using $\boldsymbol {\nabla } \boldsymbol {u}$, while it aligns with the most compressive principal strain rate, $e^+_3$, evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$. It can be concluded that the tangential strain rate is mainly determined by the strain rates of the solenoidal turbulence and their orientation with respect to the flame surface, similarly to material surfaces in incompressible flows. The apparent contradiction between (i) the independence of the normalized tangential strain rate on dilation and (ii) the strong dependence of the alignment characteristics of the principal strain rates evaluated with $\boldsymbol {\nabla } \boldsymbol {u}$ on dilatation is because dilatation due to combustion does not contribute significantly to the tangential strain rate, but influences significantly the strain rate tensor and thus the alignment of the principal strain rates of the undecomposed velocity field.

Figure 10. Alignment characteristics between the principal strain rates and the iso-surfaces of $C$, expressed by $\cos \varphi ^+_i$, as a function of $C$. The superscript $+$ denotes a quantity evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6). Symbols represent the conditional surface average for different cases as given in figure 4. (a,c,e) Hydrogen and (b,d,f) iso-octane.

Figure 11. Illustration of the directions of the principal strain rates. (a) $e_i$, evaluated using $\boldsymbol {\nabla } \boldsymbol {u}$, and (b) $e^+_i$, evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6).

It is worth noting that the effects of the amount of energy deposition on the alignment of the flame surface normals with the principal strain rates and the tangential strain rates need further investigation. In particular, for large energy deposition, the flame propagation can be significantly accelerated by the ignition, which might change the flame interactions with turbulence. As will be discussed in § 3.6, if the flame propagation speed is sufficiently large compared to the Kolmogorov velocity, no preferential alignment of the flame normal with the principal strain rates can be obtained, which will result in lower tangential strain rates.

3.5. Correlations between local tangential strain rate and small-scale turbulence

3.5.1. Tangential strain rate and small-scale turbulence evaluated using $\boldsymbol {\nabla } \boldsymbol {u}$

The initial flame kernels are relatively small compared to the turbulent integral length scale. As a result, their tangential strain rate is predominantly influenced by the local instantaneous small-scale turbulence and may not be adequately represented by the ensemble-averaged quantities of the HIT. Therefore, it is of relevance to evaluate the impact of local small-scale turbulence on the local tangential strain rate. Typically, the local small-scale turbulence is quantified by the velocity gradient tensor, its symmetric (the strain rate tensor) or skew-symmetric (the rotation tensor) parts, or their invariants (Soria et al. 1994; Blackburn, Mansour & Cantwell 1996; Elsinga & Marusic 2010; Breda & Buxton 2019). However, in this study, inspired by the scaling of the tangential strain rate with the Kolmogorov time scale, the small-scale turbulence is expressed as $(\nu /\epsilon )^{1/2}$, where $\nu$ and $\epsilon$ are the local instantaneous viscosity and turbulence dissipation rate, respectively. This definition corresponds to a local small-scale time, which is different from the Kolmogorov time ${\tau _\eta =(\nu /\bar {\epsilon })^{1/2}}$ used for the normalization in figure 4 with the average dissipation rate $\bar {\epsilon }$. Figure 12 shows the tangential strain rate as a function of the reciprocal of such local small-scale time. Both quantities are normalized with the Kolmogorov time evaluated in the unburned mixture ${\tau _\eta }$. Statistics are taken for two iso-surfaces of $C$ for each fuel, which correspond to $C$ with the maximum dilatation rate ($C=0.4$ for iso-octane and $C=0.7$ for hydrogen cf. figure 4) and negligible dilatation rate ($C=0.02$). For $C=0.02$, the correlations between the local tangential strain rate and the small-scale turbulence are almost the same for both fuels. An almost linear positive correlation can be identified for all the cases of each fuel, which agrees well with the slope of $0.28$. However, distinctly different behaviours of different cases are observed in regions with high dilatation rates. In particular, a negative correlation is observed for the slow iso-octane kernel at $0.5\tau ^0_{f}$. Figures 13 and 14 show the alignment characteristics as a function of $\tau _\eta /(\nu /\epsilon )^{1/2}$ for $C=0.02$ (negligible dilatation rate) and in the regions with high dilatation, respectively. For $C=0.02$, a similar behaviour is observed for both fuels. The flame normals preferentially align with the most compressive principal strain rate and this preferential alignment tends to increase with increasing $\tau _\eta /(\nu /\epsilon )^{1/2}$ for all the cases. This is expected, since a stronger velocity gradient means a higher likelihood of the surface normal being oriented by the flow, which results in a preferential alignment of the surface normals with the most compressive principal strain rates. However, in regions with large dilatation (figure 14), different behaviours are observed for different cases. In particular, for hydrogen flame kernels and the slow iso-octane kernel at $0.5\tau _{f}^0$, which exhibit high dilatation, $\tau _\eta \varDelta$ (figure 4), the flame normals preferentially align with the most extensive principal strain rates and this preferential alignment tends to increase with increasing $\tau _\eta /(\nu /\epsilon )^{1/2}$. Such different correlations in the presence of dilatation imply that the quantity describing the small-scale turbulence, which contains both the effects of the solenoidal turbulence and dilatation, is ‘polluted’ by the dilatation. It is hypothesized that only the solenoidal component, rather than the entire small-scale flow, is the decisive parameter and a more general behaviour is expected when only considering the solenoidal turbulence, which is consistent with the material surfaces in incompressible flows. This hypothesis and the ‘pollution’ of the dilatation in the small-scale turbulence are assessed in the next section.

Figure 12. Normalized tangential strain rate $\tau _\eta a_{t}$ as a function of small-scale turbulence, expressed by $\tau _\eta / (\nu /\epsilon )^{{1}/{2}}$. Both variables are normalized with the Kolmogorov time evaluated in the unburned mixture, $\tau _\eta$. Symbols represent the conditional surface average for different cases as given in figure 4. (a,c) Hydrogen and (b,d) iso-octane.

Figure 13. Alignment characteristics between the principal strain rates and the iso-surfaces of $C$, expressed by $\cos \varphi _i$, as a function of $\tau _\eta /(\nu /\epsilon )^{{1}/{2}}$ for $C=0.02$ (negligible dilatation rate). Symbols represent the conditional surface average for different cases as given in figure 4. (a,c,e) Hydrogen and (b,d,f) iso-octane.

Figure 14. Alignment characteristics between the principal strain rates and the iso-surfaces of $C$, expressed by $\cos \varphi _i$, as a function of $\tau _\eta /(\nu /\epsilon )^{{1}/{2}}$ for regions with high dilatation rate. Symbols represent the conditional surface average for different cases as given in figure 4. (a,c,e) Hydrogen and (b,d,f) iso-octane.

3.5.2. Tangential strain rate and small-scale turbulence evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$

In this section, quantities evaluated using the solenoidal turbulence, $\boldsymbol {\nabla } \boldsymbol {u}_{s}$, in the regions with high dilatation rate are assessed. As demonstrated in figure 15, the effects of small-scale solenoidal turbulence on the local tangential strain rate in the regions with high dilatation are almost identical for both fuels and very similar to the characteristics obtained from the iso-surface of $C=0.02$ in figure 12 with a slope close to $0.28$. The dependence of the alignment characteristics is shown in figure 16. The same behaviour is observed for different cases and is similar to the region with low dilatation in figure 13. This is remarkable since the flame response to turbulence of the two fuels is distinctly different due to the significantly different Lewis numbers (cf. table 1). In particular, the hydrogen flames feature strong thermodiffusive instabilities resulting in a very different flame topology compared with the iso-octane flames as shown in figure 3. Such general behaviour indicates that the effects of the solenoidal turbulence on the flame surface straining and the orientation of the surface are not influenced by the Lewis numbers. This general behaviour also validates the assumptions of (3.8) for the investigated flames.

Figure 15. Normalized tangential strain rate $\tau _\eta a_{t}$ as a function of small-scale turbulence, expressed by $\tau _\eta / (\nu /\epsilon ^+)^{{1}/{2}}$. The superscript $+$ denotes a quantity evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6). Both variables are normalized with the Kolmogorov time evaluated in the unburned mixture, $\tau _\eta$. Symbols represent the conditional surface average for different cases as given in figure 4. (a) Hydrogen and (b) iso-octane.

Figure 16. Alignment characteristics between the principal strain rates and the iso-surfaces of $C$, expressed by $\cos \varphi ^+_i$, as a function of $\tau _\eta /(\nu /\epsilon ^+)^{{1}/{2}}$. The superscript $+$ denotes a quantity evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6). Symbols represent the conditional surface average for different cases as given in figure 4. (a,c,e) Hydrogen and (b,d,f) iso-octane.

Dilatation changes not only the direction of the principal strain rates but also the local dissipation rate and thus the normalized local small-scale time $\tau _\eta /(\nu /\epsilon )^{1/2}$. Figure 17 shows the difference between the normalized local small-scale time $\tau _\eta /(\nu /\epsilon )^{1/2}$ evaluated using the undecomposed velocity field and $\tau _\eta /(\nu /\epsilon ^+)^{1/2}$ evaluated using the solenoidal turbulence. In regions with high dilatation, $\tau _\eta /(\nu /\epsilon )^{1/2}$ is increased. In other regions, $\tau _\eta /(\nu /\epsilon )^{1/2}$ can also be reduced by dilatation. Due to such effects of dilatation on the local velocity gradient as well as the dissipation rate, the correlation between the tangential strain rate or the alignment characteristics and $\tau _\eta /(\nu /\epsilon )^{1/2}$ is ambiguous in regions with high dilatation (figures 12 and 14).

Figure 17. Effects of dilatation on the small-scale turbulence expressed by $\tau _\eta /(\nu /\epsilon )^{1/2}$. The superscript $+$ denotes a quantity evaluated using $\boldsymbol {\nabla } \boldsymbol {u}_{s}$ in (3.6). Symbols represent the conditional surface average for different cases as given in figure 4. (a) Hydrogen and (b) iso-octane.

3.6. Consideration of the universality of the behaviour of $\tau _\eta \langle a_{t} \rangle _{s}$

With the decomposition, it has been shown that the tangential strain rate at the surfaces in premixed flames is mainly determined by the solenoidal part of the turbulence through the same mechanism as the material surfaces in incompressible flows: surfaces are oriented by the velocity gradients, which results in preferential alignments of the surface normal with the most compressive strain rate and yields a value of the normalized tangential strain rate of $\tau _\eta \langle a_{t} \rangle _{s} \approx 0.28$ (Yeung et al. 1990; Girimaji & Pope 1992). It is of practical importance to understand under which conditions this holds valid in premixed flames. The preferential alignment can be observed only if the strain rates have enough time to interact with the surface elements. For surfaces with propagating velocities much larger than the Kolmogorov velocity scale, $v_\eta$, which propagate through different turbulent eddies with different orientations very rapidly, the strain rates experienced by the surfaces are too fleeting to orient the surfaces. Girimaji & Pope (1992) investigated the straining of propagating surfaces in HIT and found that the tangential strain rate decreases with increasing propagation speed. Gauding et al. (2022) also reported a substantial decrease in the tangential strain rate of iso-surfaces of mixing scalars when the scalar diffusivity is increased. For premixed flames, the propagating velocity of the flame surface relative to the Kolmogorov velocity scale can be characterized by the Karlovitz number,

(3.14)\begin{equation} Ka = \frac{\tau^0_{f} }{ \tau_\eta } \approx \frac{(l^0_{f})^2 }{ \eta^2}. \end{equation}

The ratio of the flame speed to the Kolmogorov velocity scale is given as

(3.15)\begin{equation} \frac{s^0_{l}}{ v_\eta} = \frac{l^0_{f}/\tau^0_{f}}{l_\eta/\tau_\eta}\approx \frac{1}{\sqrt{Ka}}. \end{equation}

Therefore, for flames in the thin reaction zones regimes ($Ka>1$), where the propagation speed of the flame surface is small compared to the Kolmogorov velocity scale and the flame surface can be approximated as a material surface, the value of $\tau _\eta \langle a_{t} \rangle _{s} \approx 0.28$ is expected. For flames in the corrugated flamelet regime ($Ka<1$), the smallest eddy has less time to orient the surface and thus a lower value of the normalized tangential strain can be expected, which is supported by the results of Dopazo et al. (2015), who reported a normalized mean tangential strain rate of approximately $0.08$ for a flame with $Ka=0.68$. For flames in the broken reaction zones regime, even though the Karlovitz number is also larger than unity, the behaviour of the tangential strain rate might be different from the straining of material surfaces in incompressible flows since the flame regions of high curvature will increase, where the dilatation not only acts in the flame normal direction but also in the tangential directions according to (3.13), and the assumptions of (3.8) may be invalid. In addition, Krisman et al. (2021) have shown that for extinguishing flame kernels with $Ka>100$, significant flame–flame interactions exist, which might also change the behaviour of the tangential strain rate for flames in the broken reaction zones regime. It is worth noting that the tangential strain rate can also be influenced by the configuration. Wang et al. (2016, 2017) investigated the tangential strain rates of a premixed jet flame. They have shown that the tangential strain rate in the region close to the nozzle exit is smaller than in downstream regions due to the unsteadiness of turbulence near the nozzle exit.

4. Conclusions

The tangential strain rate and the alignment characteristics between the principal strain rates and the flame surface are investigated using direct numerical simulations of premixed hydrogen and iso-octane flames in the thin reaction zones regime under engine conditions. The investigated flames feature significantly different Lewis numbers and thus flame–turbulence interactions.

Tangential strain rates in all investigated flames show a similar average value of approximately $0.28$ when normalized with the Kolmogorov time scale. This value is not influenced by the alignment of the flame surface normal with the principal strain rates, which have been identified as the reason for the same value of the normalized tangential strain rate of $0.28$ at material surfaces in incompressible flows (Yeung et al. 1990). To investigate such a counter-intuitive behaviour in premixed flames, a decomposition approach is proposed to separate the effects of dilatation and residual solenoidal turbulence. It is found that such a behaviour is because dilatation due to combustion does not contribute significantly to the tangential strain rate but influences significantly the strain rate tensor and thus the orientation of the principal strain rates.

With the decomposition of the two effects, it has been shown that the tangential strain rate at the surfaces in premixed flames is mainly determined by the solenoidal part of the turbulence through the same mechanism as the material surfaces in incompressible flows: the surfaces are oriented by the velocity gradients, which results in preferential alignments of the surface normal with the most compressive strain rate and yields a value of the normalized tangential strain rate of approximately $0.28$. In addition, an almost linear correlation with a slope of $0.28$ between the local tangential strain rate and the local small-scale time evaluated using the solenoidal turbulence is identified.

This general behaviour is independent of the Lewis number and the reaction progress variable and is expected to hold valid for flames in the thin reaction zones regime. These are remarkable findings indicating that models of the tangential strain rate developed based on incompressible flows (Cant et al. 1991; Duclos et al. 1993; Hawkes & Cant 2001) apply also to premixed flames with different Lewis numbers. However, for the modelling, only the solenoidal turbulence or the flow parameters conditioned on the unburned mixtures should be taken into account. In current models (Chakraborty 2021), the Favre-averaged quantities are commonly used instead of the quantities conditioned on the unburned mixtures.