Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T16:04:10.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of magnetic field on the turbulent wake of a cylinder in free-surface magnetohydrodynamic channel flow

Published online by Cambridge University Press:  25 February 2014

John R. Rhoads ,
Eric M. Edlund  and
Hantao Ji
John R. Rhoads*
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA
Eric M. Edlund
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08543, USA
Hantao Ji
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA Princeton Plasma Physics Laboratory, Princeton, NJ 08543, USA
*
†Email address for correspondence: jrhoads@pppl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

Results from a free-surface magnetohydrodynamic (MHD) flow experiment are presented detailing the modification of vortices in the wake of a circular cylinder with its axis parallel to the applied magnetic field. Experiments were performed at Reynolds numbers of the order of 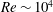${\mathit{Re}}\sim 10^4$ as the interaction parameter 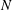${\mathit{N}}$, representing the ratio of electromagnetic forces to inertial forces, was increased through unity. The von Kármán vortex street in the wake of the cylinder was observed by simultaneously sampling the gradient of the induced electric potential, 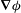$ \boldsymbol {\nabla }{\phi }$, at 16 cross-stream locations as a proxy for the streamwise fluid velocity. An ensemble of vortex velocity profiles was measured as a function of the applied magnetic field strength. Results indicate a significant change in the circulation of vortices and the deviations from the average profile as 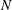${\mathit{N}}$ was increased. By sampling the fluctuations in 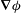$\boldsymbol {\nabla }{\phi }$ at three locations in the wake, the decay of the vortices was examined and the effective viscosity was found to decrease as 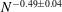${\mathit{N}}^{-0.49 \pm 0.04}$. Using temperature as a passive tracer, qualitative observations were made with an infrared (IR) camera that showed significant changes in the wake, including the absence of small-scale structures at high magnetic field strengths. Collectively, the results suggest that the reduction in effective viscosity was due to the suppression of the small-scale eddies by the magnetic field. The slope of the power spectrum was observed to change from a 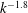$k^{-1.8}$ power law at low 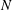${\mathit{N}}$ to a 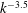$k^{-3.5}$ power law for 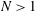${\mathit{N}}> 1$. Together, these results suggest the flow smoothly transitioned from a hydrodynamic state to a magnetohydrodynamic regime over the range of 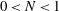$0 < {\mathit{N}}< 1$.

JFM classification

MHD and Electrohydrodynamics: MHD and Electrohydrodynamics MHD and Electrohydrodynamics: MHD turbulence Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 446 - 465
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

éeferences

Aboelkassem, Y., Vatistas, G. H. & Esmail, N. 2005 Viscous dissipation of Rankine vortex profile in zero meridional flow. Acta Mechanica Sin. 21, 550–556.Google Scholar
Alboussière, T., Uspenski, V. & Moreau, R. 1999 Quasi-2D MHD turbulent shear layers. Exp. Therm. Fluid Sci. 20, 19–24.Google Scholar
Alemany, A., Moreau, R., Sulem, P. L. & Frisch, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. Méc. 18 (2), 277–313.Google Scholar
Andreev, O., Kolesnikov, Y. & Thess, A. 2013 Visualization of the Ludford column. J. Fluid Mech. 721, 438–453.Google Scholar
Branover, H., Eidelman, A., Golbraikh, E., Kapusta, A. & Mikhailovich, B. 2004 Wave–mean flow interaction in an MHD wake behind bluff body. Fluid Dyn. Res. 35, 287–298.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136 (1), 321–374.Google Scholar
Davidson, P. A. 1997 The role of angular momentum in the magnetic damping of turbulence. J. Fluid Mech. 336, 123–150.Google Scholar
Davidson, P. A. (Ed.) 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.Google Scholar
Dousset, V. & Pothérat, A. 2008 Numerical simulations of a cylinder wake under a strong axial magnetic field. Phys. Fluids 20, 017104.Google Scholar
Dousset, V. & Pothérat, A. 2012 Characterization of the flow past a truncated square cylinder in a duct under a spanwise magnetic field. J. Fluid Mech. 691, 341–367.Google Scholar
Eckert, S., Gerbeth, G., Witke, W. & Langenbrunner, H. 2001 MHD turbulence measurements in a sodium channel flow exposed to a transverse magnetic field. Intl J. Heat Fluid Flow 22 (3), 358–364.Google Scholar
Frank, M., Barleon, L. & Müller, U. 2001 Visual analysis of two-dimensional magnetohydrodynamics. Phys. Fluids 13 (8), 2287–2295.Google Scholar
Frisch, U. (Ed.) 1995 Cambridge University Press.Google Scholar
Harris, L. P. (Ed.) 1960 Hydromagnetic channel flows. Technology Press, MIT.Google Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, S. 2013 Three-dimensional numerical simulations of magnetohydrodynamic flow around a confined circular cylinder under low, moderate, and strong magnetic fields. Phys. Fluids 25, 074102.Google Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three dimensionality in wall-bounded MHD flows. Phys. Rev. Lett. 104, 034502.Google Scholar
Klein, R., Pothérat, A. & Alferenok, A. 2009 Experiment on a confined electrically driven vortex pair. Phys. Rev. 79, 016304.Google Scholar
Kljukin, A. & Thess, A. 1998 Direct measurement of the stream-function in a quasi-two-dimensional liquid metal flow. Exp. Fluids 25, 298–304.Google Scholar
Knaepen, B. & Moreau, R. 2008 Magnetohydrodynamic turbulence at low magnetic Reynolds number. Annu. Rev. Fluid Mech. 40, 25–45.Google Scholar
Kolesnikov, Y. B. & Tsinober, A. B. 1972 Two-dimensional turbulent flow behind a circular cylinder. Magn. Gidrodin. 3, 23–31 (translation in Magnetohydrodynamics 8, 300–307).Google Scholar
Kolesnikov, Y. B. & Tsinober, A. B. 1974 Experimental investigation of two-dimensional turbulence behind a grid. Isv. Akad. Nauk. SSSR Mekh. Zhidk. Gaza 4, 146–150 (translation in Fluid Mech. 4, 621–624).Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Dokl. Akad. Nauk SSSR 30 (4), 299–303 (reprinted in Proc. R. Soc. Lond. A 434, 9–13).Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.Google Scholar
Kraichnan, R. H. 1971 Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47 (3), 525–535.Google Scholar
Lahjomri, J., Capéran, P. & Alemany, A. 1993 The cylinder wake in a magnetic field aligned with the velocity. J. Fluid Mech. 253, 421–448.Google Scholar
Morley, N. B., Burris, J., Cadwallader, L. C. & Nornberg, M. D. 2008 GaInSn usage in the research laboratory. Rev. Sci. Instrum. 79 (5), 056107.Google Scholar
Mück, B., Günther, C., Müller, U. & Bühler, L. 2000 Three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.Google Scholar
Müller, U. & Bühler, L. 2001 Magnetofluiddynamics in Channels and Containers. Springer.CrossRefGoogle Scholar
Nornberg, M. D., Ji, H., Peterson, J. L. & Rhoads, J. R. 2008 A liquid metal flume for free surface magnetohydrodynamic experiments. Rev. Sci. Instrum. 79, 094501.Google Scholar
Papailiou, D. & Lykoudis, P. 1974 Turbulent vortex streets and the entrainment mechanism of the turbulent wake. J. Fluid Mech. 62, 11–31.Google Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2005 Numerical simulations of an effective two-dimensional model for flows with a transverse magnetic field. J. Fluid Mech. 534 (1), 115–143.Google Scholar
Prokhorenko, V. Y., Roshchupkin, V. V., Pokrasin, M. A., Prokhorenko, S. V. & Kotov, V. V. 2000 Liquid gallium: potential uses as a heat-transfer agent. High Temp. USSR 38 (6), 954–968.Google Scholar
Roshko, A. 1954 On the development of turbulent wakes from vortex streets. NACA TN 3169.Google Scholar
Schmitt, F. G. 2007 About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity. C. R. Méc. 335 (9), 617–627.Google Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.Google Scholar
Sommeria, J. 1988 Electrically driven vortices in a strong magnetic field. J. Fluid Mech. 189, 553–569.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.Google Scholar
Sreenivasan, B. & Alboussière, T. 2002 Experimental study of a vortex in a magnetic field. J. Fluid Mech. 464, 287–309.Google Scholar
Strouhal, V. 1878 Ueber eine besondere Art der Tonerregung. Ann. Phys. Chem. 5 (10), 216–251.Google Scholar
Tabeling, P. 2002 Two-dimensional turbulence: a physicist approach. Phys. Rep. 362 (1), 1–62.Google Scholar
ATaylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. 223, 289–343.Google Scholar
Thess, A. & Zikanov, O. 2007 Transition from two-dimensional to three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 579, 383–412.Google Scholar
Ueno, K. & Moreau, R. 2006 Damping rate of magnetohydrodynamic vortices at low magnetic Reynolds number. Phys. Fluids 18, 025105.Google Scholar
Van Dyke, M. (Ed.) 1982 An Album of Fluid Motion. Parabolic Press.CrossRefGoogle Scholar
Wei, T. & Smith, C. R. 1986 Secondary vortices in the wake of circular cylinders. J. Fluid Mech. 169, 513–533.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K., Wu, J. & Sheridan, J. 1995 Scaling of streamwise vortices in wakes. Phys. Fluids 7 (10), 2307–2309.Google Scholar
Zikanov, O. & Thess, A. 1998 Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.Google Scholar

Rhoads et al. supplementary movie

Compilation of infrared movies showing the qualitative behavior of vortices in the wake of a cylinder as the interaction parameter, N, is increased.

Download Rhoads et al. supplementary movie(Video)
Video 9.6 MB