Article contents
Effects of Rayleigh and Weber numbers on two-layer turbulent Rayleigh–Bénard convection
Published online by Cambridge University Press: 02 October 2024
Abstract
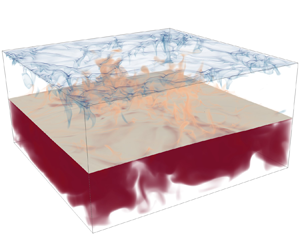
This study presents direct numerical simulation results of two-layer Rayleigh–Bénard convection, investigating the previously unexplored Rayleigh–Weber parameter space  $10^6\leq Ra\leq 10^8$ and
$10^6\leq Ra\leq 10^8$ and  $10^2\leq We\leq 10^3$. Global properties, such as the Nusselt and Reynolds numbers, are compared against the extended Grossmann–Lohse theory for two fluid layers, confirming a weak Weber number dependence for all global quantities and considerably larger Reynolds numbers in the lighter fluid. Statistics of the flow reveal that the interface fluctuates more intensely for larger Weber and smaller Rayleigh numbers, something also reflected in the increased temperature root mean square values next to the interface. The dynamics of the deformed two-fluid interface is further investigated using spectral analysis. Temporal and spatial spectrum distributions reveal a capillary wave range at small Weber and large Rayleigh numbers, and a secondary energy peak at smaller Rayleigh numbers. Furthermore, the maxima of the space–time spectra lie in an intermediate dispersion regime, between the theoretical predictions for capillary and gravity-capillary waves, showing that the gravitational energy of the interfacial waves is strongly altered by temperature gradients.
$10^2\leq We\leq 10^3$. Global properties, such as the Nusselt and Reynolds numbers, are compared against the extended Grossmann–Lohse theory for two fluid layers, confirming a weak Weber number dependence for all global quantities and considerably larger Reynolds numbers in the lighter fluid. Statistics of the flow reveal that the interface fluctuates more intensely for larger Weber and smaller Rayleigh numbers, something also reflected in the increased temperature root mean square values next to the interface. The dynamics of the deformed two-fluid interface is further investigated using spectral analysis. Temporal and spatial spectrum distributions reveal a capillary wave range at small Weber and large Rayleigh numbers, and a secondary energy peak at smaller Rayleigh numbers. Furthermore, the maxima of the space–time spectra lie in an intermediate dispersion regime, between the theoretical predictions for capillary and gravity-capillary waves, showing that the gravitational energy of the interfacial waves is strongly altered by temperature gradients.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by


