Article contents
Effects of surface tension on a floating body in two dimensions
Published online by Cambridge University Press: 23 May 2018
Abstract
A model for calculating the force profile and the moment profile of a floating body in two dimensions with an arbitrary cross-section is proposed. Three types of cross-sections with different contact angles and densities are calculated by using the model to determine the vertical and rotational equilibria and their stabilities. Results show that the model can be applied to convex floating bodies with finitely many sharp edges. The study is then extended to investigate the surface tension effects on the vertical and rotational stabilities by varying the following parameters: the radii of curvature of the solid surface at the contact lines and the size of floating body. In general, the smaller the radii of curvature the better the vertical and rotational stabilities. However, for the contact angle 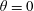 $\unicode[STIX]{x1D703}=0$ (or
$\unicode[STIX]{x1D703}=0$ (or 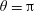 $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$ ) the radii of curvature have no effect on the vertical stability of the floating body. By varying the size of the floating body, it is found that the vertical and rotational stabilities of mesoscale floating bodies vary continuously between the stabilities of the macroscale and microscale floating bodies with other parameters remaining unchanged.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$ ) the radii of curvature have no effect on the vertical stability of the floating body. By varying the size of the floating body, it is found that the vertical and rotational stabilities of mesoscale floating bodies vary continuously between the stabilities of the macroscale and microscale floating bodies with other parameters remaining unchanged.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 9
- Cited by


