Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T03:59:13.461Z Has data issue: false hasContentIssue false
  • English
  • Français

The elastic Landau–Levich problem on a slope

Published online by Cambridge University Press:  26 November 2019

Katarzyna L. P. Warburton Open the ORCID record for Katarzyna L. P. Warburton [Opens in a new window] ,
Duncan R. Hewitt Open the ORCID record for Duncan R. Hewitt [Opens in a new window]  and
Jerome A. Neufeld
Katarzyna L. P. Warburton*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, CambridgeCB3 0WA, UK
Duncan R. Hewitt
Affiliation:
Department of Mathematics, University College London, 25 Gordon Street, LondonWC1H 0AY, UK
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, CambridgeCB3 0WA, UK BP Institute, University of Cambridge, Madingley Rise, CambridgeCB3 0EZ, UK Department of Earth Sciences, Bullard Laboratories, University of Cambridge, Madingley Rise, CambridgeCB3 0EZ, UK
*
†Email address for correspondence: klpw3@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

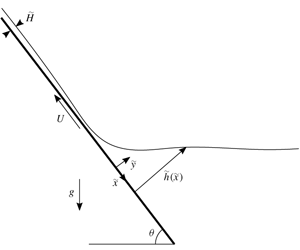
The elastic analogue of the Landau–Levich dip-coating problem, in which a plate is withdrawn from a bath of fluid on whose surface lies a thin elastic sheet, is analysed for angle of withdrawal $\unicode[STIX]{x1D703}$ to the horizontal. The flow is controlled by the elasticity number, $El$, which is a measure of the relative importance of viscous and bending stresses, and $\unicode[STIX]{x1D703}$. The leading-order solution for small $El$ is a steady profile in which the thickness of the film on the plate is found to vary as $El^{3/4}/(1-\cos \unicode[STIX]{x1D703})^{5/8}$. This prediction is confirmed in the limit $\unicode[STIX]{x1D703}\ll 1$ by comparison with numerical simulation. Finally, the circumstances under which the assumption of a steady solution is no longer valid are discussed, and the time-dependent solution is described.

JFM classification

Interfacial Flows (free surface): Thin films Low-Reynolds-number flows: Lubrication theory Materials Processing Flows: Coating
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A40
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barakat, J. M. & Shaqfeh, E. S. G. 2018 The steady motion of a closely fitting vesicle in a tube. J. Fluid Mech. 835, 721–761.CrossRefGoogle Scholar
Benilov, E. S., Chapman, S. J., McLeod, J. B., Ockendon, J. R. & Zubkov, V. S. 2010 On liquid films on an inclined plate. J. Fluid Mech. 663, 53–69.CrossRefGoogle Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.CrossRefGoogle Scholar
Deraguin, B. V. 1943 On the thickness of the liquid film adhering to the walls of a vessel after emptying. Acta Physicochim. USSR 20, 349–352.Google Scholar
Dixit, H. N. & Homsy, G. M. 2013 The elastic Landau–Levich problem. J. Fluid Mech. 732, 5–28.CrossRefGoogle Scholar
Goldstein, R. E. & Langer, S. A. 1995 Nonlinear dynamics of stiff polymers. Phys. Rev. Lett. 75, 1094–1097.CrossRefGoogle ScholarPubMed
Heap, A. & Juel, A. 2009 Bubble transitions in strongly collapsed elastic tubes. J. Fluid Mech. 633, 485–507.CrossRefGoogle Scholar
Hewitt, I. J., Balmforth, N. J. & de Bruyn, J. R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26 (1), 1–31.CrossRefGoogle Scholar
Jin, B., Acrivos, A. & Münch, A. 2005 The drag-out problem in film coating. Phys. Fluids 17 (10), 103603; arXiv:https://aip.scitation.org/doi/pdf/10.1063/1.2079927.CrossRefGoogle Scholar
Kaoui, B., Ristow, G. H., Cantat, I., Misbah, C. & Zimmerman, W. 2008 Lateral migration of a two-dimensional vesicle in unbounded Poiseuille flow. Phys. Rev. Lett. 77, 021903.Google ScholarPubMed
Landau, L. & Levich, B. 1942 Dragging of liquid by a moving plate. Acta Physicochim. USSR 7, 42–54.Google Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111, 154501.CrossRefGoogle Scholar
de Ryck, A. & Quere, D. 1998 Gravity and inertia effects in plate coating. J. Colloid Interface Sci. 203, 278–285.CrossRefGoogle ScholarPubMed
Sayag, R. & Worster, M. G. 2011 Elastic response of a grounded ice sheet coupled to a floating ice shelf. Phys. Rev. Lett. 84, 036111.Google ScholarPubMed
Seiwert, J., Quere, D. & Clanet, C. 2013 Flexible scraping of viscous fluids. J. Fluid Mech. 715, 424–435.CrossRefGoogle Scholar
Snoeijer, J. H. 2016 Analogies between elastic and capillary interfaces. Phys. Rev. Fluids 1, 060506.CrossRefGoogle Scholar
Vella, D., Aussillous, P. & Mahadevan, L. 2004 Elasticity of an interfacial particle raft. Eur. Phys. Lett. 68 (2), 212–218.CrossRefGoogle Scholar
Wilson, S. D. R. 1982 The drag-out problem in film coating theory. J. Engng Maths 16, 209–221.CrossRefGoogle Scholar