Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-10T18:27:29.519Z Has data issue: false hasContentIssue false
  • English
  • Français

The electrophoretic mobility of rod-like particles

Published online by Cambridge University Press:  26 February 2013

Ehud Yariv  and
Ory Schnitzer
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Ory Schnitzer
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: udi@technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

At finite Dukhin numbers, where Smoluchowski’s formula is inapplicable to thin-double-layer electrophoresis, the mobility of non-spherical particles is generally anisotropic. We consider bodies of revolution of otherwise arbitrary shape, where a uniformly applied electric field results in a rectilinear motion in the plane spanned by the field direction and the particle symmetry axis, as well as (for particles lacking fore–aft symmetry) rigid-body rotation about an axis perpendicular to that plane. Focusing upon slender particles, where the ratio $\epsilon $ of cross-sectional and longitudinal scales is asymptotically small, the translational and rotational mobilities are obtained as quadratures which depend upon the lengthwise distribution of the scaled cross-sectional width and the force densities associated with rigid-body motion. These mobility expressions approach finite limits as 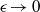$\epsilon \rightarrow 0$, yielding closed-form expressions for specific particle geometries.

JFM classification

Complex Fluids: Colloids Complex Fluids: Complex Fluids Low-Reynolds-number flows: Slender-body theory
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , R3
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allison, S., Chen, C. & Stigter, D. 2001 The length dependence of translational diffusion, free solution electrophoretic mobility, and electrophoretic tether force of rigid rod-like model duplex DNA. Biophys. J. 81 (5), 2558–2568.CrossRefGoogle ScholarPubMed
Bach, G. A., Hollingsworth, A. D. & Koch, D. L. 2002 Electrophoretic mobility of rigid rodlike particles in dilute aqueous and glycerol suspensions: comparison between theory and experiment. J. Colloid Interface Sci. 251 (1), 208–213.CrossRefGoogle ScholarPubMed
Basuray, S., Wei, H. H. & Chang, H.-C. 2010 Dynamic double layer effects on ac-induced dipoles of dielectric nanocolloids. Biomicrofluidics 4 (2).CrossRefGoogle ScholarPubMed
Brenner, H. 1964 The Stokes resistance of an arbitrary particle – IV. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.CrossRefGoogle Scholar
Buitenhuis, J. 2012 Electrophoresis of fd-virus particles: experiments and an analysis of the effect of finite rod lengths. Langmuir 28 (37), 13354–13363.CrossRefGoogle Scholar
Chen, S. B. & Koch, D. L. 1996a Electrophoresis and sedimentation of charged fibres. J. Colloid Interface Sci. 180 (2), 466–477.CrossRefGoogle Scholar
Chen, S. B. & Koch, D. L. 1996b Rheology of dilute suspensions of charged fibres. Phys. Fluids 8, 2792.CrossRefGoogle Scholar
Cole, J. D. 1968 Perturbation Methods in Applied Mathematics. Blaisdell.Google Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.CrossRefGoogle Scholar
Derjaguin, B. V. & Dukhin, S. S. 1974 Nonequilibrium double layer and electrokinetic phenomena. In Electrokinetic Phenomena (ed. Matijevic, E.). Surface and Colloid Science , vol. 7, pp. 273–336. John Wiley.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
Kang, K. & Dhont, J. K. G. 2010 Electric-field induced transitions in suspensions of charged colloidal rods. Soft Matt. 6 (2), 273–286.CrossRefGoogle Scholar
Keh, H. J. & Chen, S. B. 1993 Diffusiophoresis and electrophoresis of colloidal cylinders. Langmuir 9 (4), 1142–1149.CrossRefGoogle Scholar
Keh, H. J. & Huang, T. Y. 1993 Diffusiophoresis and electrophoresis of colloidal spheroids. J. Colloid Interface Sci. 160 (2), 354–371.CrossRefGoogle Scholar
Morrison, F. A. 1970 Electrophoresis of a particle of arbitrary shape. J. Colloid Interface Sci. 34, 210–214.CrossRefGoogle Scholar
O’Brien, R. W. 1983 The solution of the electrokinetic equations for colloidal particles with thin double layers. J. Colloid Interface Sci. 92 (1), 204–216.CrossRefGoogle Scholar
O’Brien, R. & Ward, D. 1988 The electrophoresis of a spheroid with a thin double layer. J. Colloid Interface Sci. 121 (2), 402–413.CrossRefGoogle Scholar
O’Brien, R. W. & White, L. R. 1978 Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc., Faraday Trans. 74, 1607–1626.CrossRefGoogle Scholar
Rica, R. A., Jiménez, M. L. & Delgado, Á. V. 2012 Electrokinetics of concentrated suspensions of spheroidal hematite nanoparticles. Soft Matt. 8 (13), 3596–3607.Google Scholar
Saintillan, D., Darve, E. & Shaqfeh, E. S. G. 2006 Hydrodynamic interactions in the induced-charge electrophoresis of colloidal rod dispersions. J. Fluid Mech. 563, 223–259.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012 Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86, 021503.CrossRefGoogle ScholarPubMed
Sherwood, J. D. 1981 Primary electroviscous effect in a suspension of rods. J. Fluid Mech. 111, 347–366.Google Scholar
Sherwood, J. D. 1982 Electrophoresis of rods. J. Chem. Soc., Faraday Trans. 2 78 (7), 1091–1100.CrossRefGoogle Scholar
Solomentsev, Y. & Anderson, J. L. 1994 Electrophoresis of slender particles. J. Fluid Mech. 279, 197–215.Google Scholar
Yariv, E. 2008 Slender-body approximations for electro-phoresis and electro-rotation of polarizable particles. J. Fluid Mech. 613, 85–94.CrossRefGoogle Scholar
Yariv, E., Schnitzer, O. & Frankel, I. 2011 Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory. J. Fluid Mech. 685, 306–334.Google Scholar