Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-30T22:57:09.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy balance and mixing between waves and eddies in stably stratified turbulence

Published online by Cambridge University Press:  30 July 2021

H. Lam Open the ORCID record for H. Lam [Opens in a new window] ,
A. Delache  and
F.S. Godeferd Open the ORCID record for F.S. Godeferd [Opens in a new window]
H. Lam*
Affiliation:
Université de Lyon, École Centrale de Lyon, CNRS, Université Claude Bernard Lyon 1, INSA Lyon, LMFA, UMR5509, 69130 Ecully, France
A. Delache
Affiliation:
Université de Lyon, École Centrale de Lyon, CNRS, Université Claude Bernard Lyon 1, INSA Lyon, LMFA, UMR5509, 69130 Ecully, France Université Jean Monnet, 42100 Saint-Étienne, France
F.S. Godeferd
Affiliation:
Université de Lyon, École Centrale de Lyon, CNRS, Université Claude Bernard Lyon 1, INSA Lyon, LMFA, UMR5509, 69130 Ecully, France
*
†Email address for correspondence: henri.lam@ec-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

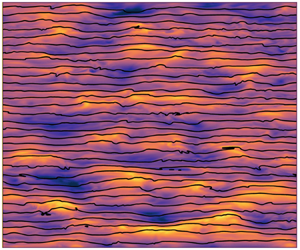
We explore the strong stratification regime of stably stratified turbulence and the intermediate regime towards the viscosity-affected stratified state. Three-dimensional velocity-density fields from direct numerical simulations are decomposed into internal gravity waves (IGWs) and eddy motion based on Riley's decomposition (Riley et al., AIP Conf. Proc., vol. 76, issue 1, 1981, pp. 79–112) extended to account for the space–time properties of waves, their modification by vertically sheared horizontal flow and the vertical mixing by eddies (Lam et al., Atmosphere, vol. 11, issue 4, 2020, p. 420). We establish the evolution equations for the IGW and eddy parts separately. Up to buoyancy Reynolds number ${Re}_b\sim 1$, we observe a large exchange of energy that pumps energy from the IGW to eddy. For ${Re}_b>1$, the IGW and eddy dynamics seem to be separate and no global exchange is observed. Our decomposition enables computation of the contributions to the mixing coefficient in terms of the IGW and eddy. At the largest ${Re}_b$ considered, the mixing due to eddies is four times that due to waves.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Wave-turbulence interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A31
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52 (24), 4410–4428.2.0.CO;2>CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Caulfield, C.P. 2021 Layering, instabilities, and mixing in turbulent stratified flows. Annu. Rev. Fluid Mech. 53 (1), 113–145.CrossRefGoogle Scholar
Cusack, J.M., Brearley, J.A., Naveira Garabato, A.C., Smeed, D.A., Polzin, K.L., Velzeboer, N. & Shakespeare, C.J. 2020 Observed eddy–internal wave interactions in the Southern Ocean. J. Phys. Oceanogr. 50 (10), 3043–3062.CrossRefGoogle Scholar
Davidson, P.A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Di Leoni, P.C., Cobelli, P.J. & Mininni, P.D. 2015 The spatio-temporal spectrum of turbulent flows. Eur. Phys. J. E 38, 136.Google Scholar
Di Leoni, P.C. & Mininni, P.D. 2015 Absorption of waves by large-scale winds in stratified turbulence. Phys. Rev. E 91 (3), 033015.CrossRefGoogle Scholar
Garanaik, A. & Venayagamoorthy, S.K. 2019 On the inference of the state of turbulence and mixing efficiency in stably stratified flows. J. Fluid Mech. 867, 323–333.CrossRefGoogle Scholar
Godeferd, F.S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6 (6), 2084–2100.CrossRefGoogle Scholar
Gregg, M.C., Sanford, T.B. & Winkel, D.P. 2003 Reduced mixing from the breaking of internal waves in equatorial waters. Nature 422 (6931), 513–515.CrossRefGoogle ScholarPubMed
Herbert, C., Marino, R., Rosenberg, D. & Pouquet, A. 2016 Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation. J. Fluid Mech. 806, 165–204.CrossRefGoogle Scholar
Ivey, G.N., Winters, K.B. & Koseff, J.R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.CrossRefGoogle Scholar
Kimura, Y. & Herring, J.R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.CrossRefGoogle Scholar
Lam, H., Delache, A. & Godeferd, F.S. 2020 Partitioning waves and eddies in stably stratified turbulence. Atmosphere 11 (4), 420.CrossRefGoogle Scholar
Le Reun, T., Favier, B., Barker, A.J. & Le Bars, M. 2017 Inertial wave turbulence driven by elliptical instability. Phys. Rev. Lett. 119 (3), 034502.CrossRefGoogle ScholarPubMed
Le Reun, T., Favier, B. & Le Bars, M. 2018 Parametric instability and wave turbulence driven by tidal excitation of internal waves. J. Fluid Mech. 840, 498–529.CrossRefGoogle Scholar
Lelong, M.-P. & Riley, J.J. 1991 Internal wave–vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.CrossRefGoogle Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.CrossRefGoogle Scholar
Lvov, Y.V., Polzin, K.L., Tabak, E.G. & Yokoyama, N. 2010 Oceanic internal-wave field: theory of scale-invariant spectra. J. Phys. Oceanogr. 40 (12), 2605–2623.CrossRefGoogle Scholar
MacKinnon, J.A., et al. 2017 Climate process team on internal wave–driven ocean mixing. Bull. Am. Meteorol. Soc. 98 (11), 2429–2454.CrossRefGoogle Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.CrossRefGoogle Scholar
Maffioli, A., Davidson, P.A., Dalziel, S.B. & Swaminathan, N. 2014 The evolution of a stratified turbulent cloud. J. Fluid Mech. 739, 229–253.CrossRefGoogle Scholar
Maffioli, A., Delache, A. & Godeferd, F.S. 2020 Signature and energetics of internal gravity waves in stratified turbulence. Phys. Rev. Fluids 5, 114802.CrossRefGoogle Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C.P., Ferrari, R., Nikurashin, M., Peltier, W.R. & Smyth, W.D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44 (12), 6296–6306.CrossRefGoogle Scholar
Moulin, F. & Flór, J.-B. 2006 Vortex–wave interaction in a rotating stratified fluid: wkb simulations. J. Fluid Mech. 563, 199–222.CrossRefGoogle Scholar
Müller, P. 1976 On the diffusion of momentum and mass by internal gravity waves. J. Fluid Mech. 77 (4), 789–823.Google Scholar
Müller, P., Holloway, G., Henyey, F. & Pomphrey, N. 1986 Nonlinear interactions among internal gravity waves. Rev. Geophys. 24 (3), 493–536.CrossRefGoogle Scholar
Olbers, D.J. 1976 Nonlinear energy transfer and the energy balance of the internal wave field in the deep ocean. J. Fluid Mech. 74 (2), 375–399.CrossRefGoogle Scholar
Osborn, T.R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.2.0.CO;2>CrossRefGoogle Scholar
Peltier, W.R. & Caulfield, C.P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.CrossRefGoogle Scholar
Riley, J.J., Metcalfe, R.W. & Weissman, M.A. 1981 Direct numerical simulations of homogeneous turbulence in density-stratified fluids. AIP Conf. Proc. 76 (1), 79–112.CrossRefGoogle Scholar
Savaro, C., Campagne, A., Linares, M.C., Augier, P., Sommeria, J., Valran, T., Viboud, S. & Mordant, N. 2020 Generation of weakly nonlinear turbulence of internal gravity waves in the Coriolis facility. Phys. Rev. Fluids 5, 073801.CrossRefGoogle Scholar
Smith, L.M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11 (6), 1608–1622.CrossRefGoogle Scholar
Smith, L.M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.CrossRefGoogle Scholar
Smyth, W.D., Moum, J.N. & Caldwell, D.R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31 (8), 1969–1992.2.0.CO;2>CrossRefGoogle Scholar
Staquet, C. & Godeferd, F.S. 1998 Statistical modelling and DNS of decaying stably stratified turbulence. Part 1. Flow energetics. J. Fluid Mech. 360, 295–340.CrossRefGoogle Scholar
Verma, M.K. 2019 Energy Transfers in Fluid Flows: Multiscale and Spectral Perspectives. Cambridge University Press.CrossRefGoogle Scholar
Waite, M.L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar

Lam Supplementary Movie

b, be, bw in the (x; z) vertical plane at mid y span for 200 successive timesteps 10Δt. Superimposed density lines are in black (density includes the background density gradient)

Download Lam Supplementary Movie(Video)
Video 7.4 MB