Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Yan
and
Chabchoub, Amin
2023.
On the formation of coastal rogue waves in water of variable depth.
Cambridge Prisms: Coastal Futures,
Vol. 1,
Issue. ,
Mendes, S.
and
Kasparian, J.
2023.
Non-homogeneous approximation for the kurtosis evolution of shoaling rogue waves.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Barman, Koushik Kanti
Chanda, Ayan
Tsai, Chia-Cheng
and
Hsu, Tai-Wen
2024.
Bragg scattering of gravity waves by a sea bed of varying depth in the presence of uniform current covered by a floating membrane.
Physics of Fluids,
Vol. 36,
Issue. 1,
Barman, Koushik Kanti
Chanda, Ayan
Tsai, Chia-Cheng
and
Mondal, Sandipan
2024.
Flexural-gravity wave interaction with undulating bottom topography in the presence of uniform current: An asymptotic approach.
Applied Mathematical Modelling,
Vol. 133,
Issue. ,
p.
41.
Aggarwal, Akshita
Barman, Koushik Kanti
Martha, Subash Chandra
and
Tsai, Chia-Cheng
2024.
Water wave interaction with ice-sheet of variable geometry in the presence of uniform current.
Physics of Fluids,
Vol. 36,
Issue. 4,
Zhang, Jie
Mendes, Saulo
Benoit, Michel
and
Kasparian, Jérôme
2024.
Effect of shoaling length on rogue wave occurrence.
Journal of Fluid Mechanics,
Vol. 997,
Issue. ,
Babu, Nitin
and
Rajendran, Suresh
2024.
Numerical investigation of triadic interactions during wave propagation over a submerged bar using a fully nonlinear numerical wave tank.
Ocean Engineering,
Vol. 311,
Issue. ,
p.
118968.
Lyu, Zuorui
2024.
Science and Engineering of Freak Waves.
p.
99.
Zhang, Jie
Ma, Yuxiang
and
Benoit, Michel
2024.
Statistical distributions of free surface elevation and wave height for out-of-equilibrium sea-states provoked by strong depth variations.
Ocean Engineering,
Vol. 293,
Issue. ,
p.
116645.
Li, Yan
and
Chabchoub, Amin
2024.
How Currents Trigger Extreme Sea Waves. The Roles of Stokes Drift, Eulerian Return Flow, and a Background Flow in the Open Ocean.
Geophysical Research Letters,
Vol. 51,
Issue. 6,
Zhang, Jian
and
Lou, Yibing
2024.
Study of wave-current coupling on offshore flexible photovoltaic foundation columns.
Frontiers in Marine Science,
Vol. 11,
Issue. ,
Kong, Liang
Lai, Chengguang
and
Li, Xuefang
2025.
Analysis of skewness/kurtosis evolution and energy modulation induced by the interaction of focused waves with barrier arrays.
Ocean Engineering,
Vol. 317,
Issue. ,
p.
120118.
Mendes, Saulo
Teutsch, Ina
and
Kasparian, Jérôme
2025.
Symmetric influence of forward and opposing tidal currents on rogue wave statistics.
Journal of Fluid Mechanics,
Vol. 1012,
Issue. ,
Moss, Charlotte S.
Schultz, David M.
Parkes, Ben
Li, Yan
and
Draycott, Samuel
2025.
Higher-harmonic contributions to surface elevation, kinematics, and wave loads in wave packets across an abrupt depth transition.
Coastal Engineering,
Vol. 197,
Issue. ,
p.
104693.
Aggarwal, Akshita
and
Martha, S. C.
2026.
Deflection of Nonperiodic Ice Sheet Due to Wave Interaction in the Presence of Current.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 148,
Issue. 1,
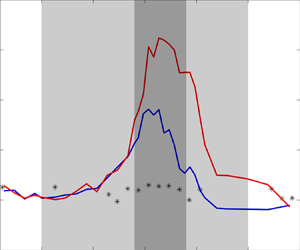
 $k_p h_2 \approx 0.5$ (
$k_p h_2 \approx 0.5$ ( $k_p$ being the peak wavenumber in the shallow area of depth
$k_p$ being the peak wavenumber in the shallow area of depth  $h_2$), although the NEP manifests, the decrease of the relative water depth does not further enhance the maximum skewness and kurtosis over the bar crest. This work highlights the nonlinear physics according to which a following current could provoke higher freak wave risk in coastal areas where modulation instability plays an insignificant role.
$h_2$), although the NEP manifests, the decrease of the relative water depth does not further enhance the maximum skewness and kurtosis over the bar crest. This work highlights the nonlinear physics according to which a following current could provoke higher freak wave risk in coastal areas where modulation instability plays an insignificant role.

