Article contents
Entrainment across a sheared density interface in a cavity flow
Published online by Cambridge University Press: 29 November 2017
Abstract
The entrainment of fluid across a sheared density interface has been examined experimentally in a purging cavity flow. In this flow, a long straight cavity with sloped entry and exit boundaries is located in the base of a straight open channel. Dense cavity fluid is entrained from the cavity into the turbulent overflow. The cavity geometry has been designed to ensure there is no separation of the overflow in the cavity region, with the goal of avoiding cavity-specific entrainment mechanisms as have been encountered in most previous experiments using similar arrangements. Results are obtained over a bulk Richardson number range 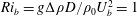 $Ri_{b}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}D/\unicode[STIX]{x1D70C}_{0}U_{b}^{2}=1$ to 19, where
$Ri_{b}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}D/\unicode[STIX]{x1D70C}_{0}U_{b}^{2}=1$ to 19, where 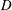 $D$ and
$D$ and 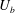 $U_{b}$ are the depth of the mixed layer and bulk velocity in the cavity, respectively. The experiments cover the Reynolds number range
$U_{b}$ are the depth of the mixed layer and bulk velocity in the cavity, respectively. The experiments cover the Reynolds number range 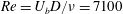 $Re=U_{b}D/\unicode[STIX]{x1D708}=7100$ to 15 100 and interface length to mixed layer depth ratios of 2.4 to 16. Particle image velocimetry and laser induced fluorescence measurements indicate the flow regime over this entire range is one dominated by the Holmboe wave instability. The non-dimensional entrainment rate,
$Re=U_{b}D/\unicode[STIX]{x1D708}=7100$ to 15 100 and interface length to mixed layer depth ratios of 2.4 to 16. Particle image velocimetry and laser induced fluorescence measurements indicate the flow regime over this entire range is one dominated by the Holmboe wave instability. The non-dimensional entrainment rate, 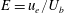 $E=u_{e}/U_{b}$ , is shown to scale with the bulk Richardson number. We find that the entrainment scaling
$E=u_{e}/U_{b}$ , is shown to scale with the bulk Richardson number. We find that the entrainment scaling 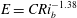 $E=CRi_{b}^{-1.38}$ applies over the entire experimental range, with no apparent dependence on interface length. The exponent in the scaling is similar to previous non-cavity-based sheared interface flows, however, the constant
$E=CRi_{b}^{-1.38}$ applies over the entire experimental range, with no apparent dependence on interface length. The exponent in the scaling is similar to previous non-cavity-based sheared interface flows, however, the constant 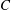 $C$ is up to an order of magnitude smaller. Close agreement is, however, obtained by instead correlating entrainment with the local gradient Richardson number centred on the interface, rather than bulk quantities. We obtain
$C$ is up to an order of magnitude smaller. Close agreement is, however, obtained by instead correlating entrainment with the local gradient Richardson number centred on the interface, rather than bulk quantities. We obtain 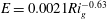 $E=0.0021Ri_{g}^{-0.63}$ for data over
$E=0.0021Ri_{g}^{-0.63}$ for data over 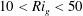 $10<Ri_{g}<50$ , where
$10<Ri_{g}<50$ , where 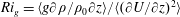 $Ri_{g}=\langle g\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x2202}z\rangle /\langle (\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z)^{2}\rangle$ . The density interface is much thinner and therefore more stable in the present flow configuration compared with other published results for the same bulk Richardson number. We suggest that our configuration ensures a sharp mixing layer profile at the upstream end of the cavity even at relatively low bulk Richardson numbers of
$Ri_{g}=\langle g\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x2202}z\rangle /\langle (\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z)^{2}\rangle$ . The density interface is much thinner and therefore more stable in the present flow configuration compared with other published results for the same bulk Richardson number. We suggest that our configuration ensures a sharp mixing layer profile at the upstream end of the cavity even at relatively low bulk Richardson numbers of 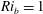 $Ri_{b}=1$ and that the reduced mixing in the Holmboe wave regime allows the interface to retain its sharp character over the cavity length, resulting in weak sensitivity to cavity length.
$Ri_{b}=1$ and that the reduced mixing in the Holmboe wave regime allows the interface to retain its sharp character over the cavity length, resulting in weak sensitivity to cavity length.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 4
- Cited by


