Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
2023.
Experimental investigation of synthetic jet control of wing rock for a flying wing aircraft.
Physics of Fluids,
Vol. 35,
Issue. 5,
Djebali, Ridha
Khilifi, Dorra
and
Ferhi, Mokhtar
2023.
Design of Experiments Investigation of Synthetic Jets Cooling Efficiency.
p.
1.
Long, Yanguang
Wang, Jinjun
and
Pan, Chong
2023.
The influence of roughness-element-spacing on turbulent entrainment over spanwise heterogeneous roughness.
Physics of Fluids,
Vol. 35,
Issue. 8,
Li, Sicheng
and
Wang, Jinjun
2024.
Entrainment of the shear layer separated from a wall-mounted fence.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Xu, Congyi
and
Wang, Jinjun
2024.
Vortex ring breakdown dominating the entrainment of a synthetic jet.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Xu, Congyi
and
Wang, Jinjun
2024.
The effect of fractal orifices on synthetic jets.
Physics of Fluids,
Vol. 36,
Issue. 11,
Gao, Tianxiang
Luo, Zhenbing
Zhou, Yan
Wu, Binrui
Kang, Ying
Peng, Can
Cheng, Pan
and
Deng, Xiong
2024.
Water droplet transport on superhydrophobic surfaces induced by the dual synthetic jets.
Physics of Fluids,
Vol. 36,
Issue. 9,
Xie, Yuanliang
Zhang, Xinxian
Xiong, Xue-Lu
and
Zhou, Yi
2024.
Temporal evolution of the turbulence interface of a turbulent plane jet.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Kohan, Khashayar F.
and
Gaskin, Susan J.
2024.
Scalar mixing and entrainment in an axisymmetric jet subjected to external turbulence.
Physics of Fluids,
Vol. 36,
Issue. 10,
Neuhaus, Lars
Wächter, Matthias
and
Peinke, Joachim
2024.
The fractal turbulent–non-turbulent interface in the atmosphere.
Wind Energy Science,
Vol. 9,
Issue. 2,
p.
439.
Mirikar, Dnyanesh
Dinesh
Kumar, Rajat
Patel, Satyanarayan
and
Yadav, Harekrishna
2025.
Synthetic jet’s flow-induced vibrations for enhanced thermal management and energy harvesting.
Applied Thermal Engineering,
Vol. 263,
Issue. ,
p.
125397.
Watanabe, Tomoaki
and
Nagata, Koji
2025.
Influences of small-scale shear instability on passive-scalar mixing in a shear-free turbulent front.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
Wang, Hao
Luo, Zhenbing
Deng, Xiong
Zhou, Yan
and
Gong, Jianyu
2025.
Enhancement of flying wing aerodynamics in crossflow at high angle of attack using dual synthetic jets.
Aerospace Science and Technology,
Vol. 156,
Issue. ,
p.
109773.
Kohan, Khashayar F.
Buxton, Oliver R. H.
and
Gaskin, Susan J.
2025.
Proceedings of the IUTAM Symposium on Turbulent/Non-Turbulent Interface in Turbulent Shear Flows.
Vol. 45,
Issue. ,
p.
194.
Xu, Congyi
and
Wang, Jinjun
2025.
Proceedings of the IUTAM Symposium on Turbulent/Non-Turbulent Interface in Turbulent Shear Flows.
Vol. 45,
Issue. ,
p.
66.
Wang, Hanbin
Xu, Yang
and
Wang, Jinjun
2025.
Experimental study on bubble pairs and induced flow fields using tomographic particle image velocimetry.
Experiments in Fluids,
Vol. 66,
Issue. 5,
Zhang, Yue
Zhou, Zhangbo
Cheng, Wan
Ding, Juchun
and
Luo, Xisheng
2025.
Fractal characteristics of interfaces in Richtmyer–Meshkov turbulence.
Physica D: Nonlinear Phenomena,
Vol. 477,
Issue. ,
p.
134711.
Price, Benjamin C.
Tang, Anthony
and
Novosselov, Igor
2025.
Parametric Study of Annular Dielectric Barrier Discharge Plasma Synthetic Jet Actuator Wall-Normal Thrust.
Yu, Yue
Fan, Dewei
Hu, Yunbing
Cheng, Zepeng
Su, Zheng
Chen, Shuang
and
Pan, Chong
2025.
Characterization of the kinematic features of cavitation bubble-induced jet flow.
International Journal of Heat and Mass Transfer,
Vol. 242,
Issue. ,
p.
126782.
Zhang, Guoyu
Wang, Xiaodong
and
Huang, Hailong
2025.
Investigation of Motive Flow Expansion Inside Steam Ejectors with Fixed Compression Ratio and Expansion Ratio.
Iranian Journal of Science and Technology, Transactions of Mechanical Engineering,
Vol. 49,
Issue. 3,
p.
1269.
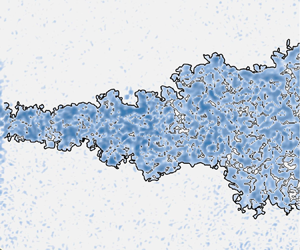
 $Re_j = 3150$. The fuzzy clustering method is applied to select an appropriate vorticity threshold to detect the TNTI. Statistically, it is revealed that the entrainment coefficients of the two jets significantly differ in the near field, while they become almost identical in the far field. Instead of the vortex ring, the ‘breakdown of the vortex ring’ enhances the entrainment in the present synthetic jet. Instantaneously, the TNTI more violently fluctuates in the near field of the synthetic jet, which leads to a larger fluctuation in the TNTI radial position, a higher fractal dimension and enhanced local entrainment. Moreover, the transition of the probability density function of the TNTI orientation from the unimodal distribution in the near field to the bimodal distribution in the far field is found in both jets. The multi-scale analysis reveals a new mechanism for the bimodal distribution caused by the TNTI-thickness-scale structures.
$Re_j = 3150$. The fuzzy clustering method is applied to select an appropriate vorticity threshold to detect the TNTI. Statistically, it is revealed that the entrainment coefficients of the two jets significantly differ in the near field, while they become almost identical in the far field. Instead of the vortex ring, the ‘breakdown of the vortex ring’ enhances the entrainment in the present synthetic jet. Instantaneously, the TNTI more violently fluctuates in the near field of the synthetic jet, which leads to a larger fluctuation in the TNTI radial position, a higher fractal dimension and enhanced local entrainment. Moreover, the transition of the probability density function of the TNTI orientation from the unimodal distribution in the near field to the bimodal distribution in the far field is found in both jets. The multi-scale analysis reveals a new mechanism for the bimodal distribution caused by the TNTI-thickness-scale structures.