Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T01:31:45.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Enumeration, orthogonality and completeness of the incompressible Coriolis modes in a sphere

Published online by Cambridge University Press:  04 February 2015

D. J. Ivers ,
A. Jackson  and
D. Winch
D. J. Ivers*
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia
A. Jackson
Affiliation:
Institut für Geophysik, ETH, Sonneggstrasse 5, 8092 Zürich, Switzerland
D. Winch
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia
*
†Email address for correspondence: david.ivers@sydney.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider incompressible flows in the rapid-rotation limit of small Rossby number and vanishing Ekman number, in a bounded volume with a rigid impenetrable rotating boundary. Physically the flows are inviscid, almost rigid rotations. We interpret the Coriolis force, modified by a pressure gradient, as a linear operator acting on smooth inviscid incompressible flows in the volume. The eigenfunctions of the Coriolis operator 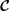$\boldsymbol{{\mathcal{C}}}$ so defined are the inertial modes (including any Rossby modes) and geostrophic modes of the rotating volume. We show 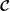$\boldsymbol{{\mathcal{C}}}$ is a bounded operator and that 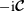$-\text{i}\boldsymbol{{\mathcal{C}}}$ is symmetric, so that the Coriolis modes of different frequencies are orthogonal. We prove that the space of incompressible polynomial flows of degree 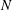$N$ or less in a sphere is invariant under 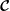$\boldsymbol{{\mathcal{C}}}$ . The symmetry of 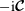$-\text{i}\boldsymbol{{\mathcal{C}}}$ thus implies the Coriolis operator is non-defective on the finite-dimensional space of spherical polynomial flows. This enables us to enumerate the Coriolis modes, and to establish their completeness using the Weierstrass polynomial approximation theorem. The fundamental tool, which is required to establish invariance of spherical polynomial flows under 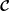$\boldsymbol{{\mathcal{C}}}$ and completeness, is that the solution of the polynomial Poisson–Neumann problem, i.e. Poisson’s equation with a Neumann boundary condition and polynomial data, in a sphere is a polynomial. We also enumerate the Coriolis modes in a sphere, with careful consideration of the geostrophic modes, directly from the known analytic solutions.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 766 , 10 March 2015 , pp. 468 - 498
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baruteau, C. & Rieutord, M. 2013 Inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 719, 47–81.Google Scholar
Bryan, G. H. 1889 The waves on a rotating liquid spheroid of finite ellipticity. Phil. Trans. R. Soc. Lond. A 180, 187–219.Google Scholar
Chossat, P. 1979 Bifurcation and stability of convective flows in a rotating or not rotating spherical shell. SIAM J. Appl. Maths 37, 624–647.Google Scholar
Cui, Z., Zhang, K. & Liao, X. 2014 On the completeness of inertial wave modes in rotating annular channels. Geophys. Astrophys. Fluid Dyn. 108, 44–59.Google Scholar
Davis, P. J. 1975 Interpolation and Approximation. Dover.Google Scholar
Dormy, E., Cardin, P. & Jault, D. 1998 MHD flow in a slightly differentially rotating spherical shell, with conducting inner core, in a dipolar magnetic field. Earth Planet. Sci. Lett. 160, 15–30.Google Scholar
Dudley, M. L. & James, R. W. 1989 Time-dependent kinematic dynamos with stationary flows. Proc. R. Soc. Lond. A 425, 407–429.Google Scholar
Friedman, A. 1982 Foundations of Modern Analysis. Dover.Google Scholar
Gans, R. F. 1974 On the Poincaré problem for a compressible medium. J. Fluid Mech. 62, 657–675.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Herreman, W. & Lesaffre, P. 2011 Stokes drift dynamos. J. Fluid Mech. 679, 32–57.Google Scholar
Hide, R. 1995 The topographic torque on a bounding surface of a rotating gravitating fluid and the excitation by core motions of decadal fluctuations in the Earth’s rotation. Geophys. Res. Lett. 22, 961–964.Google Scholar
Hollerbach, R. 1994a Magnetohydrodynamic Ekman and Stewartson layers in a rotating spherical shell. Proc. R. Soc. Lond. A 444, 333–346.Google Scholar
Hollerbach, R. 1994b Imposing a magnetic field across a nonaxisymmetric shear layer in a rotating spherical shell. Phys. Fluids 6, 2540–2544.Google Scholar
Hollerbach, R. & Proctor, M. R. E. 1993 Non-axisymmetric shear layers in a rotating spherical shell. In Theory of Solar and Planetary Dynamos (ed. Matthews, P. C., Proctor, M. R. E. & Rucklidge, A. M.), pp. 145–152. Cambridge University Press.Google Scholar
Hough, S. S. 1895 The oscillations of a rotating ellipsoidal shell containing fluid. Phil. Trans. R. Soc. Lond. A 186, 469–506.Google Scholar
Israeli, M. 1972 On trapped modes of rotating fluids in spherical shells. Stud. Appl. Maths 51, 219–237.Google Scholar
Ivanov, P. B. & Papaloizou, J. C. B. 2010 Inertial waves in rotating bodies: a WKBJ formalism for inertial modes and a comparison with numerical results. Mon. Not. R. Astron. Soc. 407, 1609–1630.CrossRefGoogle Scholar
Jones, C. A., Boronski, P., Brun, A. S., Glatzmaier, G. A., Gastine, T., Miesch, M. S. & Wicht, J. 2011 Anelastic convection-driven dynamo benchmarks. Icarus 216, 120–135.CrossRefGoogle Scholar
Kleeorin, N., Rogachevskii, I., Ruzmaikin, A., Soward, A. M. & Starchenko, S. 1997 Axisymmetric flow between differentially rotating spheres in a dipole magnetic field. J. Fluid Mech. 344, 213–244.CrossRefGoogle Scholar
Kreyszig, E. 1978 Introductory Functional Analysis with Applications. John Wiley and Sons.Google Scholar
Kudlick, M. D.1966 On transient motions in a contained rotating fluid. PhD thesis.Google Scholar
Liao, X. & Zhang, K. 2009 A new integral property of inertial waves in rotating fluid spheres. Proc. R. Soc. Lond. A 465, 1075–1091.Google Scholar
Liao, X. & Zhang, K. 2010a A new Legendre-type polynomial and its application to geostrophic flow in rotating fluid spheres. Proc. R. Soc. Lond. A 466, 2203–2217.Google Scholar
Liao, X. & Zhang, K. 2010b Asymptotic and numerical solutions of the initial value problem in rotating planetary fluid cores. Geophys. J. Intl 180, 181–192.CrossRefGoogle Scholar
Livermore, P. W. & Hollerbach, R. 2012 Successive elimination of shear layers by a hierarchy of constraints in inviscid spherical-shell flows. J. Math. Phys. 53, 073104.CrossRefGoogle Scholar
MacRobert, T. M. 1947 Spherical Harmonics An Elementary Treatise on Harmonic Functions with Applications, 2nd edn. Methuen.Google Scholar
Maxwell, J. C. 1891 A Treatise on Electricity and Magnetism, 3rd edn. Clarendon.Google Scholar
Miles, J. W. 1981 Waves in a rapidly rotating gas. J. Fluid Mech. 107, 487–497.Google Scholar
Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44, 705–719.Google Scholar
Morton, J. B. & Shaughnessy, E. J. 1972 Waves in a gas in solid-body rotation. J. Fluid Mech. 56, 277–286.Google Scholar
Nurijanyan, S., Bokhove, O. & Maas, L. R. M. 2013 A new semi-analytical solution for inertial waves in a rectangular parallelepiped. Phys. Fluids 25, 126601.Google Scholar
Pazy, A. 1983 Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer.Google Scholar
Pedlosky, J. & Greenspan, H. P. 1967 A simple laboratory model for the oceanic circulation. J. Fluid Mech. 27, 291–304.Google Scholar
Poincaré, H. 1885a Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Acta Mathematica 7, 259–380.Google Scholar
Poincaré, H. 1885b Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Bull. Astron. I 2, 109–118.Google Scholar
Poincaré, H. 1885c Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Bull. Astron. I 2, 405–413.Google Scholar
Rao, D. B. 1966 Free gravitational oscillations in rotating rectangular basins. J. Fluid Mech. 25, 523–555.Google Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics part II, time periodic flows. Geophys. Astrophys. Fluid Dyn. 59, 185–208.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.Google Scholar
Rieutord, M., Valdettaro, L. & Georgeot, B. 2002 Analysis of singular inertial modes in a spherical shell: the slender toroidal shell model. J. Fluid Mech. 463, 345–360.CrossRefGoogle Scholar
Schechter, M. 1971 Principles of Functional Analysis. Academic.Google Scholar
Soward, A. M. & Hollerbach, R. 2000 Non-axisymmetric magnetohydrodynamic shear layers in a rotating spherical shell. J. Fluid Mech. 408, 239–274.Google Scholar
Stewartson, K. 1972 On trapped oscillations of a rotating fluid in a thin spherical shell II. Tellus 24, 283–287.Google Scholar
Stewartson, K. & Rickard, J. A. 1969 Pathological oscillations of a rotating fluid. J. Fluid Mech. 35, 759–773.Google Scholar
Taylor, G. I. 1922 Tidal oscillations in gulfs and rectangular basins. Proc. Lond. Math. Soc. 20, 148–181.CrossRefGoogle Scholar
Taylor, J. B. 1963 The magneto-hydrodynamics of a rotating fluid and the Earth’s dynamo problem. Proc. R. Soc. Lond. A 274, 274–283.Google Scholar
Taylor, A. E. & Lay, D. C. 1980 Introduction to Functional Analysis, 2nd edn. John Wiley and Sons.Google Scholar
Thomson, W. 1877 On the precessional motion of a liquid. Nature 15 (379), 289–308.Google Scholar
Thomson, W. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Trefethen, L. N. 1997 Pseudospectra of linear operators. SIAM Rev. 39, 383–406.CrossRefGoogle Scholar
Zhang, K. 1993 On equatorially trapped boundary inertial waves. J. Fluid Mech. 248, 203–217.CrossRefGoogle Scholar
Zhang, K., Earnshaw, P., Liao, X. & Busse, F. H. 2001 On inertial waves in a rotating fluid sphere. J. Fluid Mech. 437, 103–119.Google Scholar
Zhang, K., Liao, X. & Earnshaw, P. 2004 The Poincaré equation: a new polynomial and its unusual properties. J. Math. Phys. 45, 4777–4790.Google Scholar