Hostname: page-component-6bf8c574d5-9f2xs Total loading time: 0 Render date: 2025-03-05T19:34:54.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium similarity solution of the turbulent transport equation along the centreline of a round jet

Published online by Cambridge University Press:  08 May 2015

H. Sadeghi ,
P. Lavoie  and
A. Pollard
H. Sadeghi
Affiliation:
Institute for Aerospace Studies, University of Toronto, Toronto, ON, M3H 5T6, Canada
P. Lavoie*
Affiliation:
Institute for Aerospace Studies, University of Toronto, Toronto, ON, M3H 5T6, Canada
A. Pollard
Affiliation:
Department of Mechanical and Materials Engineering, Queen’s University, Kingston, ON, K7L 3N6, Canada
*
†Email address for correspondence: lavoie@utias.utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

A novel similarity-based form is derived of the transport equation for the second-order velocity structure function of $\langle ({\it\delta}q)^{2}\rangle$ along the centreline of a round turbulent jet using an equilibrium similarity analysis. This self-similar equation has the advantage of requiring less extensive measurements to calculate the inhomogeneous (decay and production) terms of the transport equation. It is suggested that the normalised third-order structure function can be uniquely determined when the normalised second-order structure function, the power-law exponent of 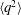$\langle q^{2}\rangle$ and the decay rate constants of 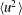$\langle u^{2}\rangle$ and 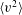$\langle v^{2}\rangle$ are available. In addition, the current analysis demonstrates that the assumption of similarity, combined with an inverse relation between the mean velocity 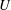$U$ and the streamwise distance 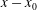$x-x_{0}$ from the virtual origin (i.e. 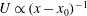$U\propto (x-x_{0})^{-1}$), is sufficient to predict a power-law decay for the turbulence kinetic energy (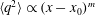$\langle q^{2}\rangle \propto (x-x_{0})^{m}$), rather than requiring a power-law decay (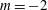$m=-2$) as an additional ad hoc assumption. On the basis of the current analysis, it is suggested that the mean kinetic energy dissipation rate, 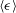$\langle {\it\epsilon}\rangle$, varies as 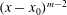$(x-x_{0})^{m-2}$. These theoretical results are tested against new experimental data obtained along the centreline of a round turbulent jet as well as previously published data on round jets for 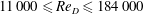$11\,000\leqslant \mathit{Re}_{D}\leqslant 184\,000$ over the range 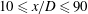$10\leqslant x/D\leqslant 90$. For the present experiments, 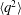$\langle q^{2}\rangle$ exhibits power-law behaviour with 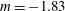$m=-1.83$. The validity of this solution is confirmed using other experimental data where 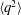$\langle q^{2}\rangle$ follows a power law with 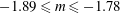$-1.89\leqslant m\leqslant -1.78$. The present similarity form of the transport equation for 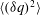$\langle ({\it\delta}q)^{2}\rangle$ is also shown to be closely satisfied by the experimental data.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 740 - 755
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-Rahman, A. A., Chakroun, W. & Al-Fahed, S. F. 1997 LDA measurements in the turbulent round jet. Mech. Res. Commun. 24, 277–288.CrossRefGoogle Scholar
Amielh, M., Djeridane, T., Anselmet, F. & Fulachier, L. 1996 Velocity near-field of variable density turbulent jets. Intl J. Heat Mass Transfer 39, 2149–2164.CrossRefGoogle Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbuelnce. J. Fluid Mech. 550, 175–184.Google Scholar
Antonia, R. A., Satyaprakash, B. A. & Hussain, A. K. F. M. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23, 695–700.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.CrossRefGoogle Scholar
Burattini, P. & Antonia, R. A. 2005 The effect of different X-wire calibration schemes on some turbulence statistics. Exp. Fluids 38, 80–89.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005a Scale-by-scale energy budget on the axis of a turbulent round jet. J. Turbul. 6, 1–11.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005b Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.Google Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.CrossRefGoogle Scholar
Corrsin, S. 1963 Turbulence: experimental methods. In Handbuch der Physik (ed. Flügge, S. & Truesdell, C. A.), pp. 524–589. Springer.Google Scholar
Danaila, L., Anselmet, F. & Antonia, R. A. 2002 An overview of the effect of large-scale inhomogeneities on small-scale turbulence. Phys. Fluids 14, 2475–2484.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 2001 Turbulent energy scale budget equations in a fully developed channel flow. J. Fluid Mech. 430, 87–109.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Fellouah, H., Ball, C. G. & Pollard, A. 2009 Reynolds number effects within the development region of a turbulent round free jet. Intl J. Heat Mass Transfer 52, 3943–3954.Google Scholar
Fellouah, H. & Pollard, A. 2010 The velocity spectra and turbulence length scale distributions in the near to intermediate regions of a round free turbulent jet. Phys. Fluids 21, 115101.Google Scholar
Ferdman, E., Otugen, M. V. & Kim, S. 2000 Effect of initial velocity profile on the development of the round jet. J. Propul. Power 4, 676–686.Google Scholar
Fulachier, L. & Antonia, R. A. 1983 Turbulent Reynolds and Péclet number re-defined. Intl Commun. Heat Mass Transfer 10 (5), 435–439.Google Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. In Advances in Turbulence (ed. George, W. K. & Arndt, R.), Springer.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids 4 (7), 1492–1509.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53, 925–942.Google Scholar
Hinze 1975 Turbulence. McGraw-Hill.Google Scholar
Hussein, H. J., Capp, S. & George, W. K. 1994 Velocity measurements in a high-Reynolds number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Lavoie, P., Burattini, P., Djenidi, P. & Antonia, R. A. 2005 Effect of initial conditions on decaying grid turbulence at low $R_{{\it\lambda}}$ . Exp. Fluids 39 (5), 865–874.CrossRefGoogle Scholar
Lumley, J. L. 1965 Interpretation of time spectra measured in high-intensity shear flows. Phys. Fluids 8, 1056–1062.Google Scholar
Malmstrom, T. G., Kirkpatrick, A. T., Christensen, B. & Knappmiller, K. D. 1997 Centreline velocity decay measurements in low-velocity axisymmetric jet. J. Fluid Mech. 246, 363–377.Google Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.Google Scholar
Pollard, A. & Uddin, M. 2007 Self-similarity of coflowing jets: the virtual origin. Phys. Fluids 19, 068103.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Quinn, W. R. 2006 Upstream nozzle shaping effects on near field flow in round turbulent free jets. Eur. J. Mech. (B/Fluids) 25, 279–301.Google Scholar
Ruffin, E., Schiestel, R., Anselmet, F., Amielh, M. & Fulachier, L. 1994 Investigation of characteristic scales in variable density turbulent jets using a secondorder model. Phys. Fluids 6, 2785–2799.Google Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2014 The effect of Reynolds number on the scaling range along the centreline of a round turbulent jet. J. Turbul. 15, 335–349.Google Scholar
Sadeghi, H. & Pollard, A. 2012 Effects of passive control rings positioned in the shear layer and potential core of a turbulent round jet. Phys. Fluids 24, 115103.Google Scholar
Taub, G. N., Lee, H., Balachandar, S. & Sherif, S. A. 2013 A direct numerical simulation study of higher order statistics in a turbulent round jet. Phys. Fluids 25, 115102.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Tong, C. & Warhaft, Z. 1994 Turbulence suppression in a jet by means of a fine ring. Phys. Fluids 6, 328–333.Google Scholar
Weisgraber, T. H. & Liepman, D. 1998 Turbulent structure during transition to self-similarity in a round jet. Exp. Fluids 24, 210–224.Google Scholar
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38, 577–612.Google Scholar
Xu, G. & Antonia, R. A. 2002 Effect of different initial conditions on a turbulent round free jet. Exp. Fluids 33, 677–683.Google Scholar
Xu, M., Pollard, A., Mi, J., Secretain, F. & Sadeghi, H. 2013 Effects of Reynolds number on some properties of a turbulent jet from a long square pipe. Phys. Fluids 25, 035102.Google Scholar