Article contents
Evaporation from a cylindrical cavity: effect of gravity on the vapour cloud
Published online by Cambridge University Press: 08 March 2024
Abstract
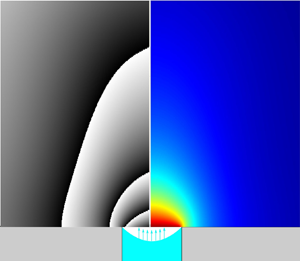
We examine the vapour cloud of a pure liquid evaporating from a millimetric cylindrical well/cavity/aperture. This is accomplished by injecting the liquid up a vertical pipe towards its outlet onto a horizontal substrate. The injection is halted before the liquid surpasses the substrate level. The resulting final state is a meniscus at or near the pipe's end. The analysis is realised by vapour interferometry (side view over the substrate) closely intertwined with simulations (including Stefan flow), which also help to fill up certain gaps in the measurements and provide computed evaporation rates. Comparison with experiment is facilitated by converting the computed vapour clouds into interferometric images, especially helpful when an inverse (Abel-type) conversion is difficult. Experiments are conducted in both microgravity (via parabolic flights) and ground conditions, thus enabling direct assessment of the role of gravity. The contrast is accentuated by a working liquid with heavy vapour (refrigerant HFE-7100), when instead of being flattened on ground the vapour cloud assumes a roughly hemispherical shape in microgravity. Furthermore, a non-trivial vapour-cloud response to the flight  ${\rm g}$-jitter (residual gravity oscillations) is unveiled,
${\rm g}$-jitter (residual gravity oscillations) is unveiled,  ${\rm g}$-jitter vibrations posing a challenge for interferometry itself. A number of undesired but curious side issues are revealed. One concerns vapour formed deep inside the pipe during rapid injection and subsequently ejected into the field of view, which is detected experimentally and quantified in terms of vapour Taylor dispersion in the pipe. Others are an injection volume anomaly and parasitic postinjection specifically observed in microgravity conditions.
${\rm g}$-jitter vibrations posing a challenge for interferometry itself. A number of undesired but curious side issues are revealed. One concerns vapour formed deep inside the pipe during rapid injection and subsequently ejected into the field of view, which is detected experimentally and quantified in terms of vapour Taylor dispersion in the pipe. Others are an injection volume anomaly and parasitic postinjection specifically observed in microgravity conditions.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 2
- Cited by


