Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T14:25:46.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of a stratified rotating shear layer with horizontal shear. Part I. Linear stability

Published online by Cambridge University Press:  13 June 2012

Eric Arobone  and
Sutanu Sarkar
Eric Arobone
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
*
†Email address for correspondence: ssarkar@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear stability analysis is used to investigate instability mechanisms for a horizontally oriented hyperbolic tangent mixing layer with uniform stable stratification and coordinate system rotation about the vertical axis. The important parameters governing inviscid dynamics are maximum shear 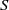, buoyancy frequency 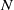, angular velocity of rotation 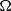and characteristic shear thickness 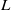. Growth rates associated with the most unstable modes are explored as a function of stratification strength 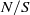and rotation strength 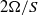. In the case of strong stratification, growth rates exhibit self-similarity of the form 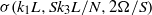. In the case of rapid rotation we also observe self-similar scaling of growth rates with respect to the vertical wavenumber and rotation rate. The unstratified cases show 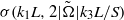dependence while the strongly stratified cases show 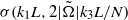dependence where 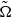represents the difference between the angular velocity of rotation and least stable anticyclonic angular velocity, 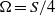. Stratification was found to stabilize the inertial instability for weak anticyclonic rotation rates. Near the zero absolute vorticity state, stratification and rotation couple in a destabilizing manner increasing the range of unstable vertical wavenumbers associated with barotropic instability. In the case of rapid rotation, stratification prevents the stabilization of low 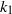, high 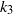modes that occurs in a homogeneous fluid. The structure of certain unstable eigenmodes and the coupling between horizontal vorticity and density fluctuations are explored to explain how buoyancy stabilizes or destabilizes inertial and barotropic modes.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 703 , 25 July 2012 , pp. 29 - 48
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.CrossRefGoogle Scholar
2. Billant, P. & Chomaz, J. M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
3. Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.CrossRefGoogle Scholar
4. Browand, F. K., Guyomar, D. & Yoon, S.-C. 1987 The behaviour of a turbulent front in a stratified fluid: experiments with an oscillating grid. J. Geophys. Res. 92 (C5), 5329–5341.Google Scholar
5. Deloncle, A., Billant, P. & Chomaz, J.-M. 2011 Three-dimensional stability of vortex arrays in a stratified and rotating fluid. J. Fluid Mech. 678, 482–510.CrossRefGoogle Scholar
6. Deloncle, A., Chomaz, J. & Billant, P. 2007 Three-dimensional stability of a horizontally sheared flow in a stably stratified fluid. J. Fluid Mech. 570, 297–305.CrossRefGoogle Scholar
7. Dunkerton, T. J. 1981 On the inertial stability of the equatorial middle atmosphere. J. Atmos. Sci. 38, 2354–2365.2.0.CO;2>CrossRefGoogle Scholar
8. Griffiths, S. D. 2003 Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60, 977–990.2.0.CO;2>CrossRefGoogle Scholar
9. Holton, J. R. 1992 An Introduction to Dynamic Meteorology. Academic.Google Scholar
10. Ivey, G. N. & Corcos, G. M. 1982 Boundary mixing in a stratified fluid. J. Fluid Mech. 121, 1–26.CrossRefGoogle Scholar
11. Johnson, J. A. 1963 The stability of shearing motion in a rotating fluid. J. Fluid Mech. 17, 337–352.CrossRefGoogle Scholar
12. Kloosterziel, R. C. & Carnevale, G. F. 2008 Vertical scale selection in inertial instability. J. Fluid Mech. 594, 249–269.CrossRefGoogle Scholar
13. Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007 Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.CrossRefGoogle Scholar
14. Liu, Y. N., Maxworthy, T. & Spedding, G. R. 1987 Collapse of a turbulent front in a stratified fluid 1. Nominally two-dimensional evolution in a narrow tank. J. Geophys. Res. 92 (C5), 5427–5433.Google Scholar
15. Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21 (106601), 1–15.CrossRefGoogle Scholar
16. Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11, 305–322.CrossRefGoogle Scholar
17. Smyth, W. D. & Peltier, W. R. 1994 Three-dimensionalization of barotropic vortices on the f-plane. J. Fluid Mech. 265, 25–64.CrossRefGoogle Scholar
18. Thorpe, S. A. 1982 On the layers produced by rapidly oscillating a vertical grid in a uniformly stratified fluid. J. Fluid Mech. 124, 391–409.CrossRefGoogle Scholar
19. Yanase, S., Flores, C., Métais, O. & Riley, J. J. 1993 Rotating free-shear flows. I. Linear stability analysis. Phys. Fluids 5 (11), 2725–2737.CrossRefGoogle Scholar