The evolution of surface quasi-geostrophic modons on sloping topography

Abstract

This work discusses modons, or dipolar vortices, propagating along sloping topography. Two different regimes exist, which are studied separately using the surface quasi-geostrophic equations. First, when the modon propagates in the direction opposite to topographic Rossby waves, steady solutions exist and a semi-analytical method is presented for calculating these solutions. Second, when the modon propagates in the same direction as the Rossby waves, a wave wake is generated. This wake removes energy from the modon, causing it to decay slowly. Asymptotic predictions are presented for this decay and found to agree closely with numerical simulations. Over long times, decaying vortices are found to break down due to an asymmetry resulting from the generation of waves inside the vortex. A monopolar vortex moving along a wall is shown to behave in a similar way to a dipole, though the presence of the wall is found to stabilise the vortex and prevent the long-time breakdown. The problem is equivalent mathematically to a dipolar vortex moving along a density front, hence our results apply directly to this case.

1. Introduction

Modons, or dipolar vortices, are exact analytical solutions to many geophysical problems and are often used to model a pair of co-propagating, oppositely signed vortices (Stern 1975; Larichev & Reznik 1976; Flierl & Haines 1994; Meleshko & van Heijst 1994; Muraki & Snyder 2007). Physically, these vortex solutions occur in both the ocean and the atmosphere, and are important for transporting fluid across large distances (Hughes & Miller 2017; Ni et al. 2020). In particular, modons are able to travel in directions that Rossby waves cannot, enabling a transfer of information that is not captured by linear wave models.

Recent analysis of satellite observations and Argo float data by Ni et al. (2020) indicates that surface modons are common features of the upper ocean, especially in energetic regions such as the Southern Ocean and the Gulf Stream. These modons were found to enhance the Ekman pumping velocity, leading to a strong vertical exchange of heat, carbon and nutrients between the ocean surface and interior. In addition to surface vortices, vortex structures may also appear on bottom boundaries. Examples of these deep-ocean vortices include lenses generated by boundary currents (Nof 1991) and eddy trains generated by the blocking of coastal-trapped waves (Rodney & Johnson 2014). These vortices may form dipolar structures through the coupling of oppositely signed vortices or through the image effect imposed by a coastal boundary (Shi & Nof 1994). Modons are similarly important in the atmosphere, where they may be involved in a variety of processes, such as atmospheric blocking (McWilliams 1980) and Madden–Julian oscillation events (Rostami & Zeitlin 2021).

The ocean and atmosphere support waves across a wide range of scales, hence moving vortices may generate a wave wake. Some families of waves – such as Rossby waves and coastal-trapped waves – travel in one direction only, resulting in an asymmetry between vortices moving with and against the wave direction. For example, on a beta-plane, eastward and westward propagating vortices behave differently (Flierl & Haines 1994). As a vortex generates waves, it loses energy, leading to a gradual change in its speed and structure. Flierl & Haines (1994) describe this decay by wave radiation of beta-plane vortices. A general framework for this process has been formulated recently, and applied to a range of dipolar vortex problems (Crowe & Johnson 2021; Johnson & Crowe 2021).

Here, we consider the evolution of modon moving along a sloping bottom boundary in the direction perpendicular to the slope. We use a three-dimensional, quasi-geostrophic (QG) model, and make the surface QG (SQG) assumption that the interior potential vorticity vanishes and hence the dynamics is controlled by the advection of density on the bottom boundary (Johnson 1978b). This system is equivalent mathematically to the case of a background horizontal density gradient (Held et al. 1995), hence our results also apply to this problem, relevant to motions in both the atmosphere and the ocean.

Section 2 notes the governing equations. Section 3 considers the case of a vortex moving in the direction opposite to the Rossby waves, described here as retrograde motion. Here, no wave wake is formed and steady vortex solutions exist. These solutions are those found by a nonlinear numerical approach in Muraki & Snyder (2007) but obtained here by a semi-analytical method that allows solutions to be found by solving a standard linear eigenvalue problem. Section 4 considers modons moving in the same direction as the Rossby waves, described as prograde. Here, a wave wake that removes energy from the vortex is generated. We present asymptotic predictions for the decay of the vortex in the limit of shallow slope. Section 5 gives numerical tests of the predictions, showing them to be valid for a range of order 1 slope parameters. Section 6 describes the long term behaviour of the decaying vortex solutions, showing that the modon structure breaks down eventually. In § 7, a monopolar vortex on a wall is shown to decay at the same rate as the dipolar solutions, but remains stable over long periods of time. Section 8 briefly discusses the results.

2. Set-up

We consider a semi-infinite layer of rotating, linearly stratified fluid of constant buoyancy frequency over a slope with constant gradient. We assume that the slope is sufficiently small for the motion to be governed by the three-dimensional QG equations, and introduce coordinates moving at speed $U$ in the direction ($x$) perpendicular to the down-slope direction ($y$). Finally, we make the SQG approximation that the interior potential vorticity (anomaly) in the layer vanishes. Our system then satisfies

(2.1)\begin{equation} \nabla^2 \psi = 0\quad\textrm{for}\ z>0, \end{equation}

where $\nabla ^2 = \partial _x^2+\partial _y^2+\partial _z^2$, with $(x,y)$ scaled on a horizontal length scale $L$, and $z$ scaled on $fL/N$ for Coriolis parameter $f$ and buoyancy frequency $N$. The evolution equation for the buoyancy on the bottom boundary gives

(2.2)\begin{equation} \left(\frac{\partial }{\partial t}-U\,\frac{\partial }{\partial x}+J\left[\psi,*\right]\right)\frac{\partial \psi}{\partial z} + w = 0\quad\textrm{on}\ z = 0, \end{equation}

which may be combined with the no-normal flow condition

(2.3)\begin{equation} w = \lambda\,\frac{\partial \psi}{\partial x} \quad\textrm{on}\ z = 0, \end{equation}

to obtain a governing equation for $\psi$ on the boundary:

(2.4)\begin{equation} \left(\frac{\partial }{\partial t}-U\,\frac{\partial }{\partial x}+J\left[\psi,*\right]\right)\frac{\partial \psi}{\partial z}+\lambda\,\frac{\partial \psi}{\partial x} = 0\quad\textrm{on} \ z = 0. \end{equation}

Here, $J[g_1,g_2] = \partial _x g_1\, \partial _y g_2 - \partial _x g_2\, \partial _y g_1$ is the Jacobian derivative, and $\lambda = (f^2L/UN)\, s$, for geometric slope $s$, is the slope in the QG limit. Details of this derivation are given in Rodney & Johnson (2014). Motion is assumed to be confined to a region near the bottom boundary, so we impose the far-field condition that $\psi \to 0$ as $z \to \infty$. This system is equivalent mathematically to the case of an SQG layer in a background buoyancy gradient, with $\lambda$ representing the constant horizontal buoyancy gradient (Held et al. 1995). The results below thus apply to modons moving along a large-scale density gradient in the atmosphere or ocean.

Throughout this work, we will consider two cases, referred to as ‘retrograde’ and ‘prograde’. Here, retrograde describes modons that are moving in the direction opposite to all topographic Rossby waves and are therefore not expected to generate a wave wake. Conversely, prograde describes modons moving with the Rossby waves, which may generate a wake.

3. Steady retrograde modons, $\mu =\lambda a/U\ge 0$

We now seek steady solutions in the form of dipolar vortices (or modons) travelling at speed $U$ in the cross-slope ($x$) direction. We consider vortices that are circular in the plane $z=0$ with (cylindrical) radius $r = a$. Taking $\partial _t = 0$, (2.4) may be written as

(3.1)\begin{equation} J\left[\psi+Uy,\frac{\partial \psi}{\partial z}+\lambda y\right] = 0\quad \textrm{on}\ z = 0, \end{equation}

which gives that

(3.2)\begin{equation} \frac{\partial \psi}{\partial z}+\lambda y = F\left(\psi+Uy\right)\quad \textrm{on}\ z = 0, \end{equation}

for some arbitrary function $F$. We will consider the class of solutions where $F$ is a linear function to obtain the Long's model (Long 1955) system

(3.3)\begin{equation} \frac{\partial \psi}{\partial z}+\lambda y ={-}\frac{K}{a}\left(\psi+Uy\right)\quad \textrm{on}\ z = 0, \end{equation}

where the value of $K$ may be different inside and outside the vortex. Far from the vortex, we require that both $\psi$ and $\partial _z \psi$ vanish, hence $K/a = -\lambda /U$ outside the vortex ($r > a$). Conversely, inside the vortex ($r < a$), $K$ must be positive to ensure that $\psi$ decays away from the boundary but will otherwise remain arbitrary until determined during the solution. From (3.3), continuity of ${\partial \psi }/{\partial z}$ and the change in the value of $K$ across the vortex boundary require that $\psi +Uy = 0$ on $r = a$. This is equivalent to the vortex boundary being a streamline in coordinates moving with the vortex. Therefore, (3.3) becomes

(3.4)\begin{equation} \frac{\partial \psi}{\partial z} =\begin{cases} -\dfrac{K}{a}\,\psi-\left(\dfrac{UK}{a}+\lambda\right) y & \textrm{for}\ z = 0,\, r < a, \\[8pt] \dfrac{\lambda}{U}\,\psi & \textrm{for}\ z = 0,\ r > a. \end{cases} \end{equation}

Steady modon solutions are now obtained by seeking solutions that satisfy (2.1) and (3.4). Following Muraki & Snyder (2007) and Johnson & Crowe (2023), we write

(3.5)\begin{equation} \psi(x,y,z) = Ua \sin\theta \int_0^\infty \hat{\psi}(\xi) J_1(\xi r/a)\exp(-\xi z/a) \,\xi \,\textrm{d} \xi, \end{equation}

where $\theta$ is the (cylindrical) polar angle, $J_1$ denotes the Bessel function of the first kind of order $1$, and $\hat {\psi }$ describes the Hankel transform of $\psi$ for $\theta ={\rm \pi} /2$ and $z = 0$. Substituting (3.5) into (3.4) gives

(3.6a)\begin{gather} \int_0^\infty \hat{\psi}(\xi) J_1(\xi s) \,\xi^2 \,\textrm{d} \xi - K\int_0^\infty \hat{\psi}(\xi) J_1(\xi s) \,\xi \,\textrm{d} \xi= \left(K+\mu\right) s \quad\textrm{for}\ s < 1, \end{gather}

(3.6b)\begin{gather}\int_0^\infty \hat{\psi}(\xi) J_1(\xi s) \,\xi^2 \,\textrm{d} \xi + \mu\int_0^\infty \hat{\psi}(\xi) J_1(\xi s) \,\xi \,\textrm{d} \xi= 0 \quad\textrm{for}\ s > 1, \end{gather}

where $s = r/a$ is the rescaled vortex radius, and $\mu = \lambda a/U$ is the rescaled slope. We now substitute

(3.7)\begin{equation} A(\xi) = \left(\xi^2+\mu\xi\right)\hat{\psi}(\xi), \end{equation}

so (3.6b) becomes

(3.8)\begin{equation} \int_0^\infty A(\xi) J_1(\xi s) \,\textrm{d} \xi = 0\quad\textrm{for}\ s > 1. \end{equation}

At this point, it is convenient to expand $A(\xi )$ in terms of Bessel functions as

(3.9)\begin{equation} A(\xi) = \sum_{n = 0}^\infty a_n J_{2n+2}(\xi), \end{equation}

for some undetermined coefficients $a_n$ (Tranter 1971; Johnson & Crowe 2023). This form allows us to exploit the integral relationship

(3.10)\begin{equation} \int_0^\infty J_{2n+2}(\xi)J_1(\xi s) \,\textrm{d}\xi = \begin{cases} \textit{R}_n(s) & \textrm{for}\ s<1, \\ 0 & \textrm{for}\ s>1, \end{cases} \end{equation}

such that (3.6b) is satisfied automatically for all choices of $a_n$. Here, $\textit {R}_n(s)$ denotes the Zernike radial function (Born & Wolf 2019), a set of degree $2n+1$ polynomials orthogonal over $s\in [0,1]$ with weight $s$. These functions are defined in Appendix B, where their properties and integral relationships discussed. Substituting for $A$ in (3.6a) gives

(3.11)\begin{equation} \int_0^\infty \frac{\xi-K}{\xi+\mu}\,A(\xi) J_1(\xi s) \,\textrm{d} \xi = (K+\mu) s \quad\textrm{for}\ s < 1, \end{equation}

hence

(3.12)\begin{equation} \sum_{n=0}^\infty a_n \int_0^\infty \frac{\xi-K}{\xi+\mu}J_{2n+2}(\xi) J_1(\xi s) \,\textrm{d} \xi = (K+\mu) s \quad\textrm{for}\ s < 1. \end{equation}

We now multiply (3.12) through by $s \textit {R}_m(s)$ and integrate over $s \in [0,1]$. Note that from (3.10), $\textit {R}_n(s)$ is the Hankel transform of $J_{2n+2}(\xi )/\xi$, so inverting this relation gives

(3.13)\begin{equation} J_{2m+2}(\xi)/\xi = \int_0^1 s \textit{R}_m(s) J_1(\xi s) \,\textrm{d} s. \end{equation}

Using (3.13), we obtain

(3.14)\begin{equation} \sum_{n = 0}^\infty a_n \int_0^\infty \frac{\xi-K}{\xi(\xi+\mu)} J_{2n+2}(\xi)J_{2m+2}(\xi) \,\textrm{d} \xi = \frac{K+\mu}{4}\,\delta_{m 0}, \end{equation}

where $m \in \{0,1,2,\dots \}$, and $\delta _{ij}$ is the Kronecker delta. Equation (3.14) takes the form of an infinite, inhomogeneous, generalised eigenvalue problem of the form

(3.15)\begin{equation} \left(\boldsymbol{\mathsf{A}}-K\boldsymbol{\mathsf{B}}\right){\boldsymbol{a}} = {\boldsymbol{c}}. \end{equation}

Here, ${\boldsymbol {a}}$ denotes the $a_n$,

(3.16)\begin{gather} {}[\boldsymbol{\mathsf{A}}]_{mn} = A_{mn} = \int_0^\infty \frac{1}{\xi+\mu}J_{2m+2}(\xi)J_{2n+2}(\xi) \,\textrm{d} \xi, \end{gather}

(3.17)\begin{gather} {}[\boldsymbol{\mathsf{B}}]_{mn} = B_{mn} = \int_0^\infty \frac{1}{\xi(\xi+\mu)} J_{2m+2}(\xi) J_{2n+2}(\xi) \,\textrm{d} \xi \end{gather}

and

(3.18)\begin{equation} [{\boldsymbol{c}}]_m = c_m = \frac{K+\mu}{4}\,\delta_{m0}. \end{equation}

The integrals in (3.16) and (3.17) are oscillatory and hence difficult to calculate directly. A method of rewriting these integrals in a non-oscillatory form that can be calculated easily is discussed in Appendix A.

The inhomogeneity of (3.15) is confined to the row $m = 0$ and may be removed by considering the boundary conditions on $s = 1$. By (3.4), we require

(3.19)\begin{equation} \frac{\partial \psi}{\partial z} = \frac{\lambda}{U}\,\psi \quad\textrm{on}\ s = 1, \end{equation}

therefore

(3.20)\begin{equation} \sum_{n = 0}^\infty a_n \int_0^\infty J_{2n+2}(\xi)J_1(\xi)\,\textrm{d}\xi = 0, \end{equation}

and hence

(3.21)\begin{equation} a_0 = \sum_{n=1}^\infty ({-}1)^{n+1}a_n. \end{equation}

We may therefore remove the first row of (3.15) and replace all instances of $a_0$ using (3.21). The resulting linear system allows us to determine the $a_n$ up to a multiplicative constant, which may be determined subsequently using the first row of (3.15). In the case $\mu = 0$, the integrals $A_{mn}$ and $B_{mn}$ may be found analytically as shown in Johnson & Crowe (2023). Our resulting linear system is

(3.22)\begin{equation} \left[ \boldsymbol{\mathsf{B}} - \frac{1}{K}\, \boldsymbol{\mathsf{A}} \right] {\boldsymbol{a}} = \boldsymbol{0}, \end{equation}

where

(3.23)\begin{equation} \tilde{A}_{mn} = A_{mn}+({-}1)^{n+1} A_{m0} \end{equation}

and

(3.24)\begin{equation} \tilde{B}_{mn} = B_{mn}+({-}1)^{n+1} B_{m0}, \end{equation}

for $m,n \in \{1,2,\dots \}$, and the eigenvectors $a_n$ are scaled using the condition

(3.25)\begin{equation} \left(A_{00}-K B_{00}\right)a_0 + \sum_{n=1}^\infty\left(A_{0n}-K B_{0n}\right)a_n = \frac{K+\mu}{4}, \end{equation}

where $a_0$ is given by (3.21). This linear system may be truncated to a finite number of terms, $m,n \in \{1,2,\dots,N\}$, to obtain numerical results using any eigensolver. We solve for $N$ eigenvalues $K$, and sets of coefficients $a_n$, with the smallest value of $K$ corresponding to the required dipolar vortex. Solutions with higher $K$ are valid and correspond to vortex solutions with a higher-order radial structure. Johnson & Crowe (2023) show that for $\lambda =0$, the higher-order solutions are unstable through pairing of the inner vortices. Higher-order solutions for $\lambda >0$ can be expected to be susceptible to the same instability, so will not be considered further. This method allows modon solutions to be found quickly and accurately, and a value $N = 19$ is sufficient to ensure that the largest neglected coefficient is less than $10^{-6}$. Our solution satisfies

(3.26)\begin{equation} \left[\frac{\partial \psi}{\partial z}-\frac{\lambda}{U}\,\psi\right]_{z = 0} = \begin{cases} -U \sin\theta \sum_{n=0}^\infty a_n \textit{R}_n(r/a) & \textrm{for}\ r< a,\\ 0 & \textrm{for}\ r>a, \end{cases} \end{equation}

and therefore, numerically, once the $a_n$ are determined, it is often easier to solve $\nabla ^2 \psi = 0$ subject to (3.26) than evaluate the Hankel transforms in (3.5). Note also that the Zernike sum in (3.26) can be evaluated from a three-term recurrence relation without requiring the form of the Zernike polynomials (Johnson & Crowe 2023). The solutions for $\lambda \ge 0$ are the same as the solutions of Muraki & Snyder (2007); however, the approach here allows solutions to be found using a compact semi-analytical approach rather than the nonlinear root-finding method of Muraki & Snyder (2007).

Figure 1 shows $\psi$ and ${\partial \psi }/{\partial z}$ for a range of non-negative values of $\lambda$. We observe that the maximum values of both $\psi$ and ${\partial \psi }/{\partial z}$ increase with increasing $\lambda$. Further, in the plots of ${\partial \psi }/{\partial z}$, we observe regions just outside $r = a$ of values that are signed oppositely to those within $r < a$. This is due to the relation ${\partial \psi }/{\partial z} = \lambda \psi /U$ for $r > a$, and corresponds to the vortex being surrounded by regions of fluid with buoyancy signed oppositely to the peaks. Evolving these solutions forward in time using the method discussed in § 5 shows that they are both steady and stable over long times.

Figure 1. Plots for (a,c,e) $\psi$ and (b,d,f) $\psi _z$ on $z = 0$ for a range of values of $\lambda$: (a,b) $\lambda = 0$, (c,d) $\lambda = 0.5$, and (e,f) $\lambda = 2$. We use $(U,a) = (1,1)$ throughout. The dashed line denotes the vortex boundary $r = a$.

We note that the maximum values of $\psi /(Ua)$ and $[{\partial \psi }/{\partial z}]/U$ on $z = 0$ depend only on $U$ and $a$ through the parameter $\mu$. This parameter dependence occurs as the integral in (3.5) depends only on $r/a$, $z/a$ and $\mu$, as $\hat {\psi }$ depends only on $\mu$. Figure 2 shows $K$, $\max [\psi ]_{z = 0}$ and $\max [{\partial \psi }/{\partial z}]_{z = 0}$ as functions of non-negative $\mu$. All quantities are observed to increase with $\mu$.

Figure 2. Plots of (a) $K$, (b) $\max [\psi ]_{z = 0}$, and (c) $\max [{\partial \psi }/{\partial z}]_{z = 0}$ as functions of $\mu = \lambda a/U$.

4. Decaying prograde modons, $\mu =\lambda a/U<0$

If a vortex has $\mu < 0$, then the integrals in (3.16) and (3.17) are singular at $\xi = |\mu |$ and do not converge. This corresponds to the case where the moving vortex generates a topographic Rossby wave wake, stating that the phase speed in the negative $x$ direction of a Rossby wave of wavenumber $|\mu |/a = |\lambda /U|$ coincides with the modon speed. Here, solutions to the governing equations are not unique unless a radiation condition is applied (Crowe & Johnson 2021; Crowe, Kemp & Johnson 2021) to ensure that no wave energy is entering the flow from the far field.

To study the case $\mu < 0$, we follow the approach of Flierl & Haines (1994) and Johnson & Crowe (2021). We begin by determining the wave field generated by a moving dipolar vortex. The energy flux into this wave field is determined and then equated to the loss of vortex energy to obtain a prediction for the vortex evolution in the case of small $\mu$. We describe this limit as the ‘weak slope’ (or equivalently, strong vortex) limit corresponding to geometric slopes satisfying $s \ll |U|\,N/f^2L$.

4.1. The wave field solution

In the far field, the vortex resembles a point dipole at the origin, so the wave field satisfies

(4.1)\begin{equation} \frac{\partial \psi}{\partial z}-\frac{\lambda}{U}\,\psi ={-}m\, \delta(x)\,\delta'(y) \quad\textrm{on}\ z = 0 \end{equation}

and

(4.2)\begin{equation} \nabla^2 \psi = 0 \quad\textrm{in}\ z > 0, \end{equation}

where $m$ denotes the dipole impulse. We now write $\kappa = -\lambda /U$, or equivalently, $\kappa = -\mu /a$, so $\kappa$ will correspond to the wavenumber of the generated wave field. Equations (4.1) and (4.2) can be solved using a two-dimensional Fourier transform in $x$ and $y$ to obtain

(4.3)\begin{equation} \psi = \frac{m}{4{\rm \pi}^2}\iint \frac{{\rm i}l}{\sqrt{k^2+l^2}-\kappa} \exp\left[ {\rm i}k x + {\rm i}ly - z\sqrt{k^2+l^2}\right] {\rm d}k \,\textrm{d} l. \end{equation}

For $\kappa >0$ (and hence $\mu < 0$), there is a singularity in the integrand of (4.3) at $k^2+l^2 = \kappa ^2$. This singularity corresponds to the appearance of topographic Rossby waves, and the integral must be evaluated such that the solution obeys the radiation condition of no disturbances propagating inwards from the far field. Our dipole solution may be written as the $y$ derivative of the monopole solution of Johnson (1978a), so

(4.4)\begin{equation} \psi = m\,\frac{\partial G}{\partial y}, \end{equation}

where

(4.5)\begin{align} G(r,\theta,z) &=\frac{1}{2{\rm \pi}\sqrt{r^2+z^2}} \nonumber\\ &\quad - \frac{\kappa}{4}\exp(-\kappa z)\left[ \mathcal{H}_0(\kappa r) + Y_0(\kappa r) + \frac{2}{\rm \pi}\int_0^{\kappa z} \frac{\exp(t)}{\sqrt{t^2+\kappa^2 r^2}} \,\textrm{d} t + \frac{8}{\rm \pi}\,S(\kappa r,\theta)\right], \end{align}

with $\mathcal {H}_0$ the zero-order Struve function, and $Y_0$ a Bessel function of the second kind. The final term, $S$, cancels the wave field ahead of any disturbance and reinforces the wave field behind the disturbance. It also appears in the treatment of barotropic flow past a cylinder on a beta-plane (McCartney 1975), and can be written as

(4.6)\begin{equation} S(\kappa r,\theta) = \sum_{k=0}^\infty \frac{\cos[(2k+1)\theta]\,{\rm J}_{2k+1}(\kappa r)}{2k+1}. \end{equation}

4.2. The wave energy flux

We now reduce to the case of small $\kappa$ and consider a semi-infinite cylinder of radius $R\gg 1$ centred on the vortex. As $\kappa$ is small, we take $R$ such that $\kappa R \ll 1$, and note that the outward energy flux through this cylinder must be independent of $R$. We are therefore able to calculate this energy flux using the streamfunction in the limit of small $\kappa r$. Using polar coordinates,

(4.7)\begin{equation} \psi = m\left[\sin\theta\,\frac{\partial G}{\partial r}+\frac{\cos\theta}{r}\,\frac{\partial G}{\partial \theta}\right], \end{equation}

hence

(4.8)\begin{align} \psi &\sim \frac{m}{\rm \pi}\left( \sin\theta\left[-\frac{r}{2(r^2+z^2)^{3/2}} + O(\kappa)\right] \right.\nonumber\\ &\quad \left.{}+ \sin\theta\cos\theta\left[ \frac{\kappa^4}{3}\,r^2 \exp(-\kappa z) + O(\kappa^6)\right] + O(\kappa^6) \right). \end{align}

The rate of change of vortex energy is given by the sum of the work done by the pressure on the cylinder and the energy advected through the cylinder. This energy loss is calculated in Appendix E and given by (E11). Using our asymptotic result from (4.8), we can calculate the rate of energy loss in the limit of small $\mu$ as

(4.9)\begin{equation} \frac{\mathrm{d} E}{\mathrm{d} t} ={-}\frac{m^2\,|U|\,\kappa^4}{3{\rm \pi}} ={-}\frac{{\rm \pi}\,|a_0|^2\,\lambda^4 a^6}{48\,|U|}, \end{equation}

hence

(4.10)\begin{equation} \frac{\mathrm{d} }{\mathrm{d} t}\left[ U^2 a^3\right] ={-}\frac{ |a_0|\,\lambda^4 a^6}{24\,|U|}, \end{equation}

where $a_0$ is defined in (3.21), and the results for the vortex energy $E$ and momentum $m$ are given in the limit of small $\mu$ in Appendix D (D3 and D9) as

(4.11a,b)\begin{equation} m = \frac{{\rm \pi}\,|a_0|\,U a^3}{4}, \quad E = \frac{{\rm \pi}\,|a_0|\,U^2 a^3}{2}. \end{equation}

4.3. Asymptotic predictions for the vortex decay

To predict the vortex decay, we will assume that the vortex form remains self-similar throughout the evolution and hence depends only on its speed, $U$ and radius $a$. Both $U$ and $a$ may vary with time, hence we need two equations involving these parameters in order to determine the evolution. Equation (4.10) corresponds to conservation of energy and is one such equation. Conservation of total momentum or potential vorticity might be expected to hold and give further equations linking $U$ and $a$. However, our previous work (Johnson & Crowe 2021) has shown that these quantities are not well conserved throughout the evolution as some fluid escapes the vortex as its radius decreases, carrying significant amounts of momentum and potential vorticity with it. This issue was resolved by following Flierl & Haines (1994) and instead considering the value of a tracer within the innermost streamline. Here, the natural choice is buoyancy, and we therefore assume that the buoyancy at the maximum of $\psi$ within the vortex is conserved. This gives

(4.12)\begin{equation} \frac{\mathrm{d} }{\mathrm{d} t}\left. \frac{\partial \psi}{\partial z}\right|_{\psi = \psi_{max}} = 0, \end{equation}

and is shown in § 5 to be a reasonable assumption. Noting that in the limit of small $\mu$, ${\partial \psi }/{\partial z} \propto U$ independently of $a$, we have

(4.13)\begin{equation} \frac{\mathrm{d} U}{\mathrm{d} t} = 0 \end{equation}

throughout the vortex evolution. Combining this result with (4.10) gives our predictions for the evolution of the vortex speed and radius as

(4.14a,b)\begin{equation} U(t) = U(t_0), \quad a(t) = a(t_0)\left[ 1+\frac{|a_0|\,a(t_0)^3 \lambda^4}{72\,|U|^3}\,(t-t_0) \right]^{{-}1/3}, \end{equation}

for some initial time $t = t_0$.

5. Numerical solutions for decaying prograde modons

We now test the predictions of § 4 using numerical simulations of (2.1) and (2.4). Solving this system directly requires an inversion of the Laplacian at each time step in order to calculate ${\partial \psi }/{\partial z}$. The value of ${\partial \psi }/{\partial z}$ on the boundary is then stepped forward using (2.4). Since $\psi$ satisfies the Laplace equation, it is standard practice to determine ${\partial \psi }/{\partial z}$ from $\psi$ using a Dirichlet-to-Neumann operator (Held et al. 1995). This avoids solving in the full three-dimensional domain and reduces our problem to two spatial dimensions. Working in Fourier space in $x$ and $y$, (2.1) becomes

(5.1)\begin{equation} \frac{\partial ^2\hat\psi}{\partial z^2} - (k^2+l^2)\, \hat\psi = 0, \end{equation}

hence

(5.2)\begin{equation} \left.\frac{\partial \hat\psi}{\partial z}\right|_{z = 0} ={-}\sqrt{k^2+l^2}\left.\hat\psi\right|_{z = 0}, \end{equation}

where the choice of sign comes from the requirement that $\psi \to 0$ as $z\to \infty$. We now define $\mathcal {D}$ to be a linear operator that acts in Fourier space as $\hat {\mathcal {D}} = -\sqrt {k^2+l^2}$. Therefore, $\mathcal {D}$ may be thought of as both the fractional Laplacian operator $\mathcal {D} = -\sqrt {-\nabla ^2}$ and the required Dirichlet-to-Neumann map ${\partial \psi }/{\partial z} = \mathcal {D}\,\psi$. We therefore solve the two-dimensional system

(5.3)\begin{equation} \left(\frac{\partial }{\partial t}-C\,\frac{\partial }{\partial x}+J\left[\psi,*\right]\right)\mathcal{D}\psi+\lambda\,\frac{\partial \psi}{\partial x} ={-}\nu\,\nabla^4 \mathcal{D}\psi \quad\textrm{on}\ z = 0, \end{equation}

where hyperdiffusion is included for numerical stability. Here, $C$ denotes the speed of the moving coordinates, hence taking $C = U$ results in the vortex remaining centred on the origin.

Equation (5.3) is solved using spectral methods via the Dedalus package (Burns et al. 2020). We use a doubly periodic two-dimensional domain of size $102.4 \times 102.4$, with $4096$ grid points in each direction, and expand $\psi$ in a Fourier basis in both directions. Time stepping is performed using a $3-\epsilon$ order implicit–explicit Runge–Kutta scheme. Our simulations are initialised by placing an SQG modon at the centre of the domain using the solutions from § 3 with $\lambda = 0$ and $(U,a) = (-1,1)$. Simulations are run for $\lambda \in \{0,0.2,0.4,0.6,0.8,1.0\}$ over the time interval $t \in [0,50]$. This time interval is chosen as it ensures that the generated waves do not have sufficient time to loop around the domain and interact with the vortex.

Initially, over a short time interval $t \in [0,t_0]$, the vortex solution adjusts to the non-zero slope parameter $\lambda$ and begins to generate a wave field. To compare our simulations with the theoretical predictions of (4.14a,b), we take a value $t_0 = 5$ and calculate $a(t_0)$ and $U(t_0)$ from our numerical data. This value of $t_0$ is found to be sufficient such that the transient motions arising from the initial adjustment have decayed.

Figure 3 shows $\psi$ from our numerical simulations at times $t = t_0 = 5$ and $t = 40$ for slope $\lambda = 0.4$. The formation of a wave wake can be seen clearly. Results are shown in coordinates moving with speed $C = -1$. Since the vortex speed $U$ changes slightly during the initial adjustment phase, the vortex does not remain at the origin throughout the evolution. Figure 4 shows the maximum values of $\psi$ and ${\partial \psi }/{\partial z}$ as functions of time for each simulation run. Our asymptotic decay predictions from (4.14a,b) are shown as dashed lines and found to give accurate predictions for the decay, even for the cases where $\lambda$ is order 1. The value of $\max [{\partial \psi }/{\partial z}]$ is found to be well conserved throughout the evolution – varying by less than $3\,\%$ for most cases – justifying the assumptions made in § 4.3. The curves for $\lambda \ge 0.6$ in figure 4 are shown over the limited interval $t \in [t_0, t_\lambda ]$, where $t_\lambda = 40, 25, 20$, respectively, for $\lambda = 0.6, 0.8, 1.0$. Outside these intervals, the dipolar vortices break down and the assumption of self-similar vortex structure is no longer valid. This breakdown is explored in § 6.

Figure 3. The streamfunction $\psi$ as a function of $(x,y)$ for $\lambda = 0.4$ at times (a) $t = 5$ and (b) $t = 40$.

Figure 4. Plots of (a) $\max [\psi ]$ and (b) $\max [{\partial \psi }/{\partial z}]$ from numerical simulations for $\lambda \in \{0, 0.2, 0.4, 0.6, 0.8, 1\}$. Results are shown as functions of time $t$ from $t_0 = 5$ onwards, and all curves are normalised by their initial value. Dashed lines denote the asymptotic predictions of (4.14a,b).

6. Vortex breakdown

Numerical solutions reveal that over long times, decaying dipolar vortices with $\mu < 0$ will break down into a pair of monopolar vortices. When this breakdown occurs, the structures cease to move purely in the east–west direction and instead follow complex trajectories. This breakdown occurs sooner for steeper slopes, i.e. sooner for larger values of $\lambda$ and $|\mu |$.

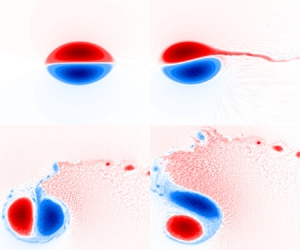
Examination of simulation results suggests that the breakdown occurs through the development of waves inside the vortex. These waves lead to an asymmetry that causes the two halves of the dipole to split. The wave amplitude is larger for larger values of $|\mu |$, hence the breakdown occurs sooner. Figure 5 shows the breakdown of a dipolar vortex for $(U,a,\lambda ) = (-1,1,0.8)$ that occurs from approximately $t_\lambda = 25$. The breakdown is seen most clearly in the buoyancy field ${\partial \psi }/{\partial z}$, hence we plot buoyancy rather than streamfunction $\psi$. We observe that after an asymmetry develops in the dipolar structure, streamers of buoyancy (and potential vorticity) are stripped away from each side. These streamers later roll up into lines of small monopolar vortices that interact with each other through a series of merging and splitting events, as predicted by the theory of SQG turbulence (Held et al. 1995). As the initial asymmetry results in the two halves having different vortex strengths, they cease to move together in a straight line. Instead, the modified vortex pair deflects south before following a complicated path as the vortex strength changes due to subsequent interactions. As expected, waves are still generated post-breakdown if there is a significant disturbance moving westwards. Supplementary movie 1 available at https://doi.org/10.1017/jfm.2023.607 shows the full evolution of the modon for the case $\lambda = 0.8$ depicted in figure 5. A similar breakdown due to asymmetric instability is observed by Makarov & Kizner (2011) and Jalali & Dritschel (2020) for the case of oppositely signed vortex patches.

Figure 5. Plots of the surface buoyancy ${\partial \psi }/{\partial z}$ for $\lambda = 0.8$ and (a) $t = 25$, (b) $t = 27$, (c) $t = 29$, (d) $t = 30$, (e) $t = 35$, and (f) $t = 40$. The breakdown of a dipolar vortex into two monopolar vortices can be seen clearly.

Snyder et al. (2007) considered the evolution of SQG modons in a primitive equation model and observed that waves could form within the modon. These inertia-gravity waves were found to result from both initial adjustment and imbalance, and were stronger for larger Rossby numbers. In our case, we are considering a balanced model and, as such, expect that waves occur through a combination of initial adjustment and topographic effects. A small disturbance advected in the up-slope $y$ direction by the interior flow can increase in vorticity due to the conservation of potential vorticity. This magnification of small disturbances may in turn lead to vortex breakdown.

7. Stabilisation by a coastal boundary

By the image effect, we would expect a monopolar vortex moving along a coastal boundary to behave in the same way as a dipolar modon and be described by the same solutions as discussed in §§ 2–4. In particular, we expect steady solutions for retrograde vortices, and a decay rate for prograde vortices that follows (4.14a,b) in the limit of small $\lambda$.

To test our decay prediction, we rerun our Dedalus simulations on the half-domain $(x,y) \in [-51.2,51.2]\times [-51.2,0]$ using a sine basis in the $y$ direction to enforce the condition that $\psi = 0$ along the wall $y = 0$. All other parameters and analysis techniques remain unchanged. Figure 6 shows the maximum values of $\psi$ and ${\partial \psi }/{\partial z}$ as functions of time for each simulation run. Our asymptotic prediction from (4.14a,b) is included as a dashed line and found to be consistent with the observed decay, even for order $1$ values of $\lambda$. Figure 7 shows the surface streamfunction and buoyancy for the case $\lambda = 0.8$ at two different times. The formation of the wave field can be seen clearly in the plots of $\psi$, while the close-up plots of ${\partial \psi }/{\partial z}$ show the decrease in vortex size at later times. We observe that at late times and larger values of $\lambda$, the vortex shape becomes elliptical, with a shorter semi-radius in the $y$ direction. This will reduce the validity of the assumption that the vortex remains self-similar throughout the evolution, and may explain partially why the decay prediction is less accurate in these cases. Supplementary movie 2 shows the full evolution of the coastal vortex for the case $\lambda = 0.8$ depicted in figure 7.

Figure 6. As figure 4 for a monopolar vortex moving along a coastal boundary.

Figure 7. The time evolution of a monopolar vortex on a wall for $\lambda = 0.8$. We plot the surface streamfunction $\psi$ for (a) $t = 10$ and (b) $t = 40$, and the surface buoyancy ${\partial \psi }/{\partial z}$ for (c) $t = 10$ and (d) $t = 40$.

A major difference observed between the dipolar vortices and the coastal monopoles is that the vortex breakdown discussed in § 6 does not occur during the monopole evolution. This is likely a consequence of the enforced symmetry of the image vortex across the line $y = 0$, and suggests that the breakdown of the dipoles occurs due to the growth of an asymmetry between the regions of positive and negative vorticity.

8. Discussion and conclusions

Here, we study the evolution of a propagating modon on sloping topography using a combination of numerical and analytical approaches. Since Rossby waves propagate along the slope in one direction only, there are two regimes of interest: retrograde motion, where the modon propagates oppositely to the waves, and prograde motion, where the waves and modon propagate in the same direction.

In steady retrograde motion, no wave wake is generated as there are no waves with phase speed matching the speed of the vortex. Steady vortex solutions exist that can be found by expanding the vortex solution in terms of Zernike radial functions. The coefficients of the Zernike functions, and the internal wavenumber of the modon $K$, follow by solving a linear algebraic eigenvalue problem. Increasing the slope gradient is found to increase the velocity of fluid within the vortex and create regions surrounding the vortex core where the buoyancy is signed oppositely to the closest peak.

In prograde motion, waves are generated with a phase speed matching the speed of the vortex. As no energy enters the system from upstream, a unique solution can be found in which a wave wake is generated behind the vortex. This wake removes energy from the vortex in the form of a radial energy flux from the vortex into the wave field. Under the assumption of weak slope, we derive predictions for the decay of the vortex radius with time. In contrast with the similar problem of a one-layer QG dipole on a beta-plane (Flierl & Haines 1994; Crowe & Johnson 2020), the vortex speed is predicted to remain unchanged throughout the decay. Our asymptotic predictions are tested numerically and found to closely match simulation results. In particular, we find that decay predictions remain accurate even for order 1 values of the slope parameter. Over long times, we observe that modons break down as asymmetries develop between the two halves of the dipole. These asymmetries lead to the formation of two coupled monopolar vortices and are predicted to occur due to wave-like oscillations within the modon.

Solutions corresponding to a monopolar vortex moving along a coastal boundary can be found using the method of images. These solutions are identical to our dipolar solutions over the reduced domain and follow a similar vortex decay in the prograde case. Over long times, the vortex breakdown observed for prograde modons does not occur, likely as a result of the enforced symmetry of the wall.

Finite-depth effects or non-constant stratification are easily incorporated into our model and change only the form of the vertical dependence in (3.5), as discussed in Appendix C. This modifies the eigenvalue problem in (3.15), though solutions can be found using the same method. Our modon solutions decay exponentially away from the boundary, and as such, finite-depth effects are unlikely to be significant unless the fluid layer is very shallow compared to the vortex radius. In the prograde case, a finite depth will also discretise the wave spectrum such that a sufficiently shallow layer will admit only barotropic wave modes. These generalisations will be studied in future work.

Our assumption of SQG dynamics imposes several limitations on our results. In particular, we can study only small topographic slopes (by the assumption of small vertical velocity) and flows with no interior potential vorticity. QG models also struggle to represent accurately the turbulent boundary layers found in the ocean and atmosphere. The common approach of imposing an Ekman pumping velocity on the boundary could be included easily into our model; however, most of the limitations of QG can be avoided only by considering a full three-dimensional primitive equation model. Comparison between three-dimensional numerical simulations and our QG results would allow any discrepancies to be identified, but is beyond the scope of this study.

Due to the widespread nature of dipolar vortices in both the ocean and atmosphere, our results and predictions may be applicable to a range of phenomena. For example, modons have been used as simple models for various atmospheric phenomena, such as localised jets at the tropopause and atmospheric blocks (Muraki & Snyder 2007), so our results may be relevant for modelling these flows or understanding their generation of Rossby waves. Further, the mathematical system that we study is identical to the case of a surface modon moving on a density gradient in the along-gradient direction. As such, our predictions may be relevant to mesoscale vortices moving along density fronts. While our set-up makes the unrealistic assumptions that the front is weak and very wide compared with the vortex, our qualitative predictions may be applicable to more realistic fronts that typically have strong density gradients and widths comparable to mesoscale vortices. Therefore, our results may be of some relevance to propagating modons in the Gulf Stream and Southern Ocean, both very energetic regions of the ocean containing a high density of modons and fronts (Orsi, Whitworth & Nowlin 1995; Ni et al. 2020).