Published online by Cambridge University Press: 16 January 2019
A new set of exact coherent states in the form of a travelling wave is reported in plane channel flow. They are continued over a range in 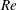 $Re$ from approximately
$Re$ from approximately 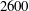 $2600$ up to
$2600$ up to 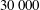 $30\,000$, an order of magnitude higher than those discovered in the transitional regime. This particular type of exact coherent states is found to be gradually more localised in the near-wall region on increasing the Reynolds number. As larger spanwise sizes
$30\,000$, an order of magnitude higher than those discovered in the transitional regime. This particular type of exact coherent states is found to be gradually more localised in the near-wall region on increasing the Reynolds number. As larger spanwise sizes 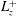 $L_{z}^{+}$ are considered, these exact coherent states appear via a saddle-node bifurcation with a spanwise size of
$L_{z}^{+}$ are considered, these exact coherent states appear via a saddle-node bifurcation with a spanwise size of 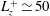 $L_{z}^{+}\simeq 50$ and their phase speed is found to be
$L_{z}^{+}\simeq 50$ and their phase speed is found to be 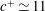 $c^{+}\simeq 11$ at all the Reynolds numbers considered. Computation of the eigenspectra shows that the time scale of the exact coherent states is given by
$c^{+}\simeq 11$ at all the Reynolds numbers considered. Computation of the eigenspectra shows that the time scale of the exact coherent states is given by 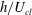 $h/U_{cl}$ in channel flow at all Reynolds numbers, and it becomes equivalent to the viscous inner time scale for the exact coherent states in the limit of
$h/U_{cl}$ in channel flow at all Reynolds numbers, and it becomes equivalent to the viscous inner time scale for the exact coherent states in the limit of 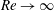 $Re\rightarrow \infty$. The exact coherent states at several different spanwise sizes are further continued to a higher Reynolds number,
$Re\rightarrow \infty$. The exact coherent states at several different spanwise sizes are further continued to a higher Reynolds number, 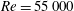 $Re=55\,000$, using the eddy-viscosity approach (Hwang & Cossu, Phys. Rev. Lett., vol. 105, 2010, 044505). It is found that the continued exact coherent states at different sizes are self-similar at the given Reynolds number. These observations suggest that, on increasing Reynolds number, new sets of self-sustaining coherent structures are born in the near-wall region. Near this onset, these structures scale in inner units, forming the near-wall self-sustaining structures. With further increase of Reynolds number, the structures that emerged at lower Reynolds numbers subsequently evolve into the self-sustaining structures in the logarithmic region at different length scales, forming a hierarchy of self-similar coherent structures as hypothesised by Townsend (i.e. attached eddy hypothesis). Finally, the energetics of turbulent flow is discussed for a consistent extension of these dynamical systems notions to high Reynolds numbers.
$Re=55\,000$, using the eddy-viscosity approach (Hwang & Cossu, Phys. Rev. Lett., vol. 105, 2010, 044505). It is found that the continued exact coherent states at different sizes are self-similar at the given Reynolds number. These observations suggest that, on increasing Reynolds number, new sets of self-sustaining coherent structures are born in the near-wall region. Near this onset, these structures scale in inner units, forming the near-wall self-sustaining structures. With further increase of Reynolds number, the structures that emerged at lower Reynolds numbers subsequently evolve into the self-sustaining structures in the logarithmic region at different length scales, forming a hierarchy of self-similar coherent structures as hypothesised by Townsend (i.e. attached eddy hypothesis). Finally, the energetics of turbulent flow is discussed for a consistent extension of these dynamical systems notions to high Reynolds numbers.