The diffraction of an initially one-dimensional plane expansion wave over a 90° corner was explored using experiment and numerical simulation. Unlike studies of shock diffraction, expansion wave diffraction has hardly been documented previously. The planar expansion wave was produced in a shock tube by bursting a diaphragm. Two independent parameters were identified for study: (i) the initial diaphragm shock tube pressure ratio, which determines the strength (pressure ratio) of the expansion, and (ii) the position of the diaphragm from the apex of the 90° corner, which determines the width of the wave. The experimentation only considered variation in the shock tube pressure ratio whereas the simulation varied both parameters. A Navier–Stokes solver with Menter’s shear stress transport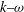 
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k\mbox{--}\omega $ turbulence model was found to adequately model the overall flow field. A number of major flow features were identified occurring in the vicinity of the corner. These were: a shear layer that originated by flow separation at the apex of the corner; a vortex within a separation bubble that remained attached to the wall, in sharp contrast to what happens in the shock wave diffraction case, where the vortex convects downstream; and a reflected compression wave arising from perturbation signals generated by the diffraction. For a narrow-width expansion wave existing prior to diffraction, the reflected compression wave steepens into an outwardly propagating, weak cylindrical shock wave. Regions of supersonic flow are identified surrounding the bubble and can extend downstream depending on the pressure ratio. Another major flow feature identified in some cases was an oblique shock located near the separation bubble. A large wake region is evident immediately downstream of the bubble and appears to consist of two distinct layers. The experimental results showed large-scale turbulent structures within the separation bubble, and shear layer instability and vortex shedding from the separation bubble were also evident.
