Published online by Cambridge University Press: 25 January 2016
We experimentally study linear and nonlinear inertial waves in a spherical shell with a radius ratio of 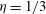 ${\it\eta}=1/3$. The shell rotates with a mean angular velocity
${\it\eta}=1/3$. The shell rotates with a mean angular velocity 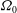 ${\it\Omega}_{0}$ around its vertical axis. This rotation is overlaid by a time-periodic libration of the inner sphere in the range
${\it\Omega}_{0}$ around its vertical axis. This rotation is overlaid by a time-periodic libration of the inner sphere in the range 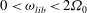 $0<{\it\omega}_{lib}<2{\it\Omega}_{0}$ to excite inertial waves with a defined frequency. In the first part, we investigate linear inertial waves. The influence of the libration amplitude and the libration frequency on the waves and further the efficiency of the forcing to excite linear inertial waves will be discussed. For this, qualitative data from Kalliroscope visualisation in a meridional laser plane, as well as quantitative particle image velocimetry (PIV) data in a horizontal plane, have been analysed. A simple two-dimensional ray-tracing model is applied for the meridional plane to interpret the visualisations with respect to energy focusing and wave attractors. For sufficiently high/low libration amplitudes/frequencies, the Stewartson layer, a vertical shear layer tangential to the inner sphere’s equator, becomes unstable. This so-called ‘supercritical’ regime, where centrifugal and shear instabilities occur, allows for nonlinear wave coupling. PIV analyses in the horizontal laser plane in the corotating frame show low-frequency structures that correspond to Rossby-wave instabilities of the Stewartson layer. Some of these are travelling retrograde and are trapped near the Stewartson layer, others are travelling prograde filling the whole gap outside the Stewartson layer. Since libration can be viewed as a time-periodic variation of differential rotation, we assume that these two different structures are related to either the retrograde
$0<{\it\omega}_{lib}<2{\it\Omega}_{0}$ to excite inertial waves with a defined frequency. In the first part, we investigate linear inertial waves. The influence of the libration amplitude and the libration frequency on the waves and further the efficiency of the forcing to excite linear inertial waves will be discussed. For this, qualitative data from Kalliroscope visualisation in a meridional laser plane, as well as quantitative particle image velocimetry (PIV) data in a horizontal plane, have been analysed. A simple two-dimensional ray-tracing model is applied for the meridional plane to interpret the visualisations with respect to energy focusing and wave attractors. For sufficiently high/low libration amplitudes/frequencies, the Stewartson layer, a vertical shear layer tangential to the inner sphere’s equator, becomes unstable. This so-called ‘supercritical’ regime, where centrifugal and shear instabilities occur, allows for nonlinear wave coupling. PIV analyses in the horizontal laser plane in the corotating frame show low-frequency structures that correspond to Rossby-wave instabilities of the Stewartson layer. Some of these are travelling retrograde and are trapped near the Stewartson layer, others are travelling prograde filling the whole gap outside the Stewartson layer. Since libration can be viewed as a time-periodic variation of differential rotation, we assume that these two different structures are related to either the retrograde 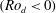 $(Ro_{d}<0)$ or the prograde
$(Ro_{d}<0)$ or the prograde 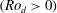 $(Ro_{d}>0)$ phase of the libration cycle. The experimental results confirm theoretical, numerical as well as other experimental studies on Stewartson-layer instabilities.
$(Ro_{d}>0)$ phase of the libration cycle. The experimental results confirm theoretical, numerical as well as other experimental studies on Stewartson-layer instabilities.