Published online by Cambridge University Press: 14 August 2013
Experiments for gravity currents generated from an instantaneous buoyancy source propagating on an inclined boundary in the slope angle range  ${0}^{\circ } \leq \theta \leq {9}^{\circ } $ are reported. While the flow patterns for gravity currents on
${0}^{\circ } \leq \theta \leq {9}^{\circ } $ are reported. While the flow patterns for gravity currents on 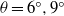 $\theta = {6}^{\circ } , {9}^{\circ } $ are qualitatively different from those on
$\theta = {6}^{\circ } , {9}^{\circ } $ are qualitatively different from those on 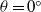 $\theta = {0}^{\circ } $ , similarities are observed in the acceleration phase for the flow patterns between
$\theta = {0}^{\circ } $ , similarities are observed in the acceleration phase for the flow patterns between 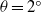 $\theta = {2}^{\circ } $ and
$\theta = {2}^{\circ } $ and 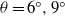 $\theta = {6}^{\circ } , {9}^{\circ } $ and in the deceleration phase, the patterns for gravity currents on
$\theta = {6}^{\circ } , {9}^{\circ } $ and in the deceleration phase, the patterns for gravity currents on 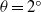 $\theta = {2}^{\circ } $ are found similar to those on
$\theta = {2}^{\circ } $ are found similar to those on  $\theta = {0}^{\circ } $ . Previously, it was known that the front location history in the deceleration phase obeys a power-relationship, which is essentially an asymptotic form of the solution to thermal theory. We showed that this power-relationship applies only in the early stage of the deceleration phase, and when gravity currents propagate into the later stage of the deceleration phase, viscous effects become more important and the front location data deviate from this relationship. When the power-relationship applies, it is found that at
$\theta = {0}^{\circ } $ . Previously, it was known that the front location history in the deceleration phase obeys a power-relationship, which is essentially an asymptotic form of the solution to thermal theory. We showed that this power-relationship applies only in the early stage of the deceleration phase, and when gravity currents propagate into the later stage of the deceleration phase, viscous effects become more important and the front location data deviate from this relationship. When the power-relationship applies, it is found that at 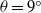 $\theta = {9}^{\circ } $ ,
$\theta = {9}^{\circ } $ , 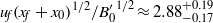 ${u}_{f} {({x}_{f} + {x}_{0} )}^{1/ 2} / {{ B}_{0}^{\prime } }^{1/ 2} \approx 2. 8{ 8}_{- 0. 17}^{+ 0. 19} $ , which changes to
${u}_{f} {({x}_{f} + {x}_{0} )}^{1/ 2} / {{ B}_{0}^{\prime } }^{1/ 2} \approx 2. 8{ 8}_{- 0. 17}^{+ 0. 19} $ , which changes to  $2. 8{ 6}_{- 0. 13}^{+ 0. 13} $ at
$2. 8{ 6}_{- 0. 13}^{+ 0. 13} $ at 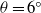 $\theta = {6}^{\circ } $ ,
$\theta = {6}^{\circ } $ ,  $2. 5{ 4}_{- 0. 07}^{+ 0. 08} $ at
$2. 5{ 4}_{- 0. 07}^{+ 0. 08} $ at 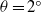 $\theta = {2}^{\circ } $ , and
$\theta = {2}^{\circ } $ , and  $1. 5{ 1}_{- 0. 07}^{+ 0. 07} $ on a horizontal boundary, where
$1. 5{ 1}_{- 0. 07}^{+ 0. 07} $ on a horizontal boundary, where 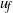 ${u}_{f} $ is the front velocity,
${u}_{f} $ is the front velocity, 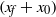 $({x}_{f} + {x}_{0} )$ is the front location measured from the virtual origin, and
$({x}_{f} + {x}_{0} )$ is the front location measured from the virtual origin, and  ${ B}_{0}^{\prime } $ is the released buoyancy. Our results indicate that in the slope angle range
${ B}_{0}^{\prime } $ is the released buoyancy. Our results indicate that in the slope angle range 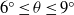 ${6}^{\circ } \leq \theta \leq {9}^{\circ } $ , the asymptotic relationship between the front velocity and front location in the deceleration phase is not sensitive to the variation of slope angle. In the late deceleration phase when the front location data deviate from the power-relationship, we found that the flow patterns for
${6}^{\circ } \leq \theta \leq {9}^{\circ } $ , the asymptotic relationship between the front velocity and front location in the deceleration phase is not sensitive to the variation of slope angle. In the late deceleration phase when the front location data deviate from the power-relationship, we found that the flow patterns for 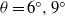 $\theta = {6}^{\circ } , {9}^{\circ } $ are dramatically different from those for
$\theta = {6}^{\circ } , {9}^{\circ } $ are dramatically different from those for 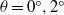 $\theta = {0}^{\circ } , {2}^{\circ } $ . For high slope angles, i.e.
$\theta = {0}^{\circ } , {2}^{\circ } $ . For high slope angles, i.e.  $\theta = {6}^{\circ } , {9}^{\circ } $ , the edge of the gravity current head experiences a large upheaval and enrolment by ambient fluid towards the end of the deceleration phase, while for low slope angles, i.e.
$\theta = {6}^{\circ } , {9}^{\circ } $ , the edge of the gravity current head experiences a large upheaval and enrolment by ambient fluid towards the end of the deceleration phase, while for low slope angles, i.e. 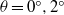 $\theta = {0}^{\circ } , {2}^{\circ } $ , the gravity current head maintains a more streamlined shape without violent mixing with ambient fluid throughout the course of gravity current propagation. Our findings indicate two plausible routes to the finale of a gravity current event.
$\theta = {0}^{\circ } , {2}^{\circ } $ , the gravity current head maintains a more streamlined shape without violent mixing with ambient fluid throughout the course of gravity current propagation. Our findings indicate two plausible routes to the finale of a gravity current event.