Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T09:03:51.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow and heat transfer in convectively unstable turbulent channel flow with solid-wall heat conduction

Published online by Cambridge University Press:  19 September 2014

Anirban Garai ,
Jan Kleissl  and
Sutanu Sarkar
Anirban Garai
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, CA 92093, USA
Jan Kleissl*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, CA 92093, USA
Sutanu Sarkar
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, CA 92093, USA
*
†Email address for correspondence: jkleissl@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Most turbulent coherent structures in a convectively unstable atmospheric boundary layer are caused by or manifested in ascending warm fluid and descending cold fluids. These structures not only cause ramps in the air temperature timeseries, but also imprint on the underlying solid surface as surface temperature fluctuations. The coupled flow and heat transport mechanism was examined through direct numerical simulation (DNS) of a channel flow allowing for realistic solid–fluid thermal coupling. The thermal activity ratio (TAR; the ratio of thermal inertias of fluid and solid), and the thickness of the solid domain were found to affect the solid–fluid interfacial temperature variations. The solid–fluid interface with large (small) thermal activity ration behaves as an isoflux (isothermal) boundary. For the range of parameters considered here (Grashof number, 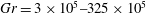$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Gr} = 3\times 10^5\text {--} 325\times 10^5$; 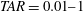$\textit {TAR} = 0.01\text {--}1$; solid thickness normalized by heat penetration 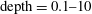$\text {depth} = 0.1\text {--}10$), the solid thermal properties and thickness influence the fluid temperature only in the viscous or conduction region while the convective forcing influences the turbulent flow. Flow structures influence the interfacial temperature more effectively with increasing TAR and solid thickness compared with a constant temperature boundary condition. The change of channel flow structures with increasing convective instability is examined and the concomitant change of thermal patterns is quantified. Despite large differences in friction Reynolds and Richardson number between the DNS and atmospheric observations, similarities in the flow features were observed.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Convection: Buoyancy-driven instability Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 57 - 81
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: NASA Ames Research Center, Moffett Field, CA 94035, USA.

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamic in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.Google Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Balick, L. K., Jeffery, C. A. & Henderson, B. 2003 Turbulence induced spatial variation of surface temperature in high resolution thermal IR satellite imagery. Proc. SPIE 4879, 221–230.Google Scholar
Ballard, J. R., Smith, J. A. & Koenig, G. G. 2004 Toward a high temporal frequency grass canopy thermal IR model for background signatures. Proc. SPIE 5431, 251–259.Google Scholar
De Bruin, H. A. R., Kohsiek, W. & Van Den Hurk, J. J. M. 1993 A verification of some methods to determine the fluxes of momentum, sensible heat, and water vapour using standard deviation and structure parameter of scalar meteorological quantities. Boundary-Layer Meteorol. 63, 231–257.CrossRefGoogle Scholar
Brutsaert, W. 1975 A theory for local evapotranspiration (or heat transfer) from rough and smooth surfaces at ground level. Water Resour. Res. 11, 543–550.CrossRefGoogle Scholar
Carslaw, H. S. & Jaeger, J. C. 1959 Conduction of Heat in Solids. Oxford University Press.Google Scholar
Christen, A. & Voogt, J. A.2009 Linking atmospheric turbulence and surface temperature fluctuations in a street canyon. The 7th International Conference on Urban Climate Paper A3-6. The International Association for Urban Climate.Google Scholar
Christen, A. & Voogt, J. A.2010 Inferring turbulent exchange process in an urban street canyon from high–frequency thermography. The 9th Symposium on the Urban Environment, Paper J3A.3. American Meteorological Society, MA, USA.Google Scholar
Chu, C. R., Parlange, M. B., Katul, G. G. & Albertson, J. D. 1996 Probability density functions of turbulent velocity and temperature in the atmospheric surface layer. Water Resour. Res. 32, 1681–1688.Google Scholar
Cohn, S. A., Mayor, S. D., Grund, C. J., Weckwerth, T. M. & Sneff, C. 1998 The lidars in flat terrain (LIFT) experiment. Bull. Am. Meteorol. Soc. 79, 1329–1343.2.0.CO;2>CrossRefGoogle Scholar
Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37, 1–30.Google Scholar
Derksen, D. S. 1974 Thermal infrared pictures and mapping of microclimate. Neth. J. Agric. Sci. 22, 119–132.Google Scholar
Drobinski, P., Brown, R. A., Flamant, P. H. & Pelon, J. 1998 Evidence of organized large eddies by ground based Doppler lidar, sonic anemometer and sodar. Boundary-Layer Meteorol. 88, 343–361.Google Scholar
Duchaine, D., Corpron, A., Pons, L., Moureau, V., Nicoud, F. & Poinsot, T. 2009 Development and assessment of a coupled strategy for conjugate heat transfer with large eddy simulation: application to a cooled turbine blade. Intl J. Heat Fluid Flow 30, 1129–1141.CrossRefGoogle Scholar
Gao, W., Shaw, R. H. & Paw U, K. T. 1989 Observation of organized structure in turbulent flow within and above a forest canopy. Boundary-Layer Meteorol. 47, 349–377.Google Scholar
Garai, A. & Kleissl, J. 2011 Air and surface temperature coupling in the convective atmospheric boundary layer. J. Atmos. Sci. 68, 2945–2954.Google Scholar
Garai, A. & Kleissl, J. 2013 Interaction between coherent structures and surface temperature and its effect on ground heat flux in an unstably stratified boundary layer. J. Turbul. 14 (8), 1–23.CrossRefGoogle Scholar
Garai, A., Pardyjak, E., Steenveld, G. J. & Kleissl, J. 2013 Surface temperature and surface layer turbulence in a convective boundary layer. Boundary-Layer Meteorol. 148, 51–72.CrossRefGoogle Scholar
Gurka, R., Liberzon, A. & Hetsroni, G. 2004 Detecting coherent patterns in a flume by using PIV and IR imaging technique. Exp. Fluids 37, 230–236.Google Scholar
Hetsroni, G., Kowalewski, T. A., Hu, B. & Mosyak, A. 2001 Tracking of coherent thermal structures on a heated wall by means of infrared thermography. Exp. Fluids 30, 286–294.Google Scholar
Hetsroni, G. & Rozenblit, R. 1994 Heat transfer to a liquid–solid mixture in a flume. Intl J. Multiphase Flow 20, 671–689.CrossRefGoogle Scholar
Högström, U. L. F. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. Boundary-Layer Meteorol. 42, 55–78.Google Scholar
Hunt, J. C. R., Vrieling, A. J., Nieuwstadt, F. T. M. & Fernando, H. J. S. 2003 The influence of the thermal diffusivity of the lower boundary on eddy motion in convection. J. Fluid Mech. 491, 183–205.CrossRefGoogle Scholar
Iida, O. & Kasagi, N. 1997 Direct numerical simulation of unstably stratified turbulent channel flow. Trans. ASME J. Heat Transfer 119, 53–61.Google Scholar
Jiménez, J. 2012 Cascade in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.CrossRefGoogle Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24, 1541–1544.CrossRefGoogle Scholar
Kaimal, J. C. & Businger, J. A. 1970 Case studies of a convective plume and a dust devil. J. Appl. Meteorol. 9, 612–620.Google Scholar
Kaimal, J. C., Wyngaard, J. C., Haugen, D. A., Cote, O. R. & Izumi, Y. 1976 Turbulence structure in the convective boundary layer. J. Atmos. Sci. 33, 2152–2169.2.0.CO;2>CrossRefGoogle Scholar
Katul, G. G., Poggi, D., Cava, D. & Finnigan, J. J. 2006a The relative importance of ejections and sweeps to momentum transfer in the atmospheric boundary layer. Boundary-Layer Meteorol. 120, 367–375.Google Scholar
Katul, G. G., Porporato, A., Cava, D. & Siqueria, M. B. 2006b An analysis of intermittency, scaling, and surface renewal in atmospheric surface layer turbulence. Physica D 215, 117–126.Google Scholar
Katul, G. G., Schieldge, J., Hsieh, C. I. & Vidakovic, B. 1998 Skin temperature perturbations induced by surface layer turbulence above a grass surface. Water Resour. Res. 3, 1265–1274.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–136.Google Scholar
Kleissl, J., Hong, S. H. & Hendrickx, J. M. H. 2009 New Mexico scintillometer network in support of remote sensing and hydrologic and meteorological models. Bull. Am. Meteorol. Soc. 90, 207–218.Google Scholar
LeMone, M. A. 1973 The structure and dynamic of horizontal roll vortices in the planetary boundary layer. J. Atmos. Sci. 30, 1077–1091.Google Scholar
Lenschow, D. H. & Boba Stankov, B. 1986 Length scales in the convective boundary layer. J. Atmos. Sci. 43, 1198–1209.Google Scholar
Lothon, M., Lenschow, D. H. & Mayor, S. D. 2006 Coherence and scale of vertical velocity in the convective boundary layer from a Doppler lidar. Boundary-Layer Meteorol. 121, 521–536.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akkad. Nauk SSSR Geophiz. Inst. 24, 163–187.Google Scholar
Morinishi, Y., Tamano, S. & Nakamura, E. 2007 New scaling of turbulence statistics for incompressible thermal channel flow with different total heat flux gradients. Intl J. Heat Mass Transfer 50, 1781–1789.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_{\tau } = 590$ . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Paulson, C. A. 1970 The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 9, 857–861.2.0.CO;2>CrossRefGoogle Scholar
Paw U, K. T., Qiu, J., Su, H.-B., Watanabe, T. & Brunet, Y. 1995 Surface renewal analysis: a new method to obtain scalar fluxes. Agric. Forest Meteorol. 77, 119–137.CrossRefGoogle Scholar
Pierce, B., Moin, P. & Sayadi, T. 2013 Application of vortex identification schemes to direct numerical simulation data of a transitional boundary layer. Phys. Fluids 25, 015102.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. pp. 1–771. Cambridge University Press.CrossRefGoogle Scholar
Raasch, S. & Etling, D. 1991 Numerical simulation of rotating turbulent thermal convection. Beitr. Phys. Atmos. 64, 185–199.Google Scholar
Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smoothwall turbulent boundary layers. J. Fluid Mech. 108, 363–382.Google Scholar
Renno, N. O., Abreu, V. J., Koch, J., Smith, P. H., Hartogensis, O. K., De Bruin, H. A. R., Burose, D., Delory, G. T., Farrell, W. M., Watts, C. J., Garatuza, J., Parker, M. & Carswell, A. 2004 MATADOR 2002: a pilot experiment on convective plumes and dust devils. J. Geophys. Res. 109, E07001.Google Scholar
Schols, J. L. J. 1984 The detection and measurement of turbulent structures in the atmospheric surface layer. Boundary-Layer Meteorol. 29, 39–58.Google Scholar
Schols, J. L. J., Jansen, A. E. & Krom, J. G. 1985 Characteristics of turbulent structures in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 33, 173–196.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent covection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Taylor, R. J. 1958 Thermal structures in the lowest layers of the atmosphere. Austral. J. Phys. 11, 168–176.CrossRefGoogle Scholar
Tiselj, I., Bergant, R., Mavk, M., Bajsić, I. & Hetsroni, G. 2001 DNS of turbulent heat transfer in channel flow with heat conduction in the solid wall. Trans. ASME J. Heat Transfer 123, 849–857.CrossRefGoogle Scholar
Verzicco, R. & Sreenivasan, K. R. 2008 A comparison of turbulent thermal convection between conditions of constant temperature and constant heat flux. J. Fluid Mech. 595, 203–219.Google Scholar
Vogt, R.2008 Visualisation of turbulent exchange using thermal camera. 18th Symposium on Boundary Layer and Turbulence, Paper 8B.1. American Meteorological Society, MA, USA.Google Scholar
Wang, X., Castillo, L. & Araya, G. 2008 Temperature scalings and profiles in forced convection turbulent boundary layers. Trans. ASME J. Heat Transfer 130, 021701.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
Wicker, L. J. & Skamarock, W. C. 2002 Time-splitting methods for elastic models using forward time schemes. Mon. Weath. Rev. 130, 2088–2097.Google Scholar
Wilczak, J. M. & Businger, J. A. 1983 Thermally indirect motions in the convective atmospheric boundary layer. J. Atmos. Sci. 40, 343–358.Google Scholar
Wilczak, J. M. & Tillman, J. E. 1980 The three-dimensional structure of convection in the atmospheric boundary layer. J. Atmos. Sci. 37, 2424–2443.Google Scholar
Williamson, J. H. 1980 Low storage Runge–Kutta schemes. J. Comput. Phys. 35, 48–56.Google Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity and the budgets of shear stress and heat flux. J. Atmos. Sci. 28, 1171–1182.Google Scholar
Young, G. S. 1988a Turbulence strucutre of the convective boundary layer. Part I: variability of normalized turbulence statistics. J. Atmos. Sci. 45, 712–719.2.0.CO;2>CrossRefGoogle Scholar
Young, G. S. 1988b Turbulence strucutre of the convective boundary layer. Part II: phoenix 78 aircraft observations of thermals and their environment. J. Atmos. Sci. 45, 727–735.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanism for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar