Article contents
Flow past finite cylinders of constant curvature
Published online by Cambridge University Press: 05 January 2018
Abstract
Wake visualization experiments were conducted on a finite curved cylinder whose plane of curvature is aligned with the free stream. The stagnation face of the cylinder is oriented concave or convex to the flow at 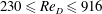 $230\leqslant Re_{D}\leqslant 916$, where
$230\leqslant Re_{D}\leqslant 916$, where 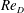 $Re_{D}$ is the cylinder Reynolds number and the curvature is constant and ranges from a straight cylinder to a quarter-ring. While the magnitude of the local angle of incidence to the flow is the same for both orientations, the contrast in their wakes demonstrates a violation of a common approximation known as the ‘independence principle’ for curved cylinders. Vortex shedding always occurred for the convex-oriented cylinder for the Reynolds-number range investigated, along most of the cylinder span, at a constant vortex shedding angle. In contrast, a concave-oriented cylinder could exhibit multiple concurrent wake regimes along its span: two shedding regimes (oblique, normal) and two non-shedding regimes. The occurrence of these wake regimes depended on the curvature, aspect ratio and Reynolds number. In some cases, vortex shedding was entirely suppressed, particularly at higher curvatures. In the laminar wake regime, increasing the curvature or decreasing the aspect ratio restricts vortex shedding to smaller regions along the span of the cylinder. Furthermore, the local angle of incidence where vortex shedding occurs is self-similar across cylinders of the same aspect ratio and varying curvature. After the wake transitions to turbulence, the vortex shedding extends along most of the cylinder span. The difference in the wakes between the concave and convex orientations is attributed to the spanwise flow induced by the finite end conditions, which reduces the generation of spanwise vorticity and increases the incidence of non-shedding and obliquely shedding wakes for the concave cylinder.
$Re_{D}$ is the cylinder Reynolds number and the curvature is constant and ranges from a straight cylinder to a quarter-ring. While the magnitude of the local angle of incidence to the flow is the same for both orientations, the contrast in their wakes demonstrates a violation of a common approximation known as the ‘independence principle’ for curved cylinders. Vortex shedding always occurred for the convex-oriented cylinder for the Reynolds-number range investigated, along most of the cylinder span, at a constant vortex shedding angle. In contrast, a concave-oriented cylinder could exhibit multiple concurrent wake regimes along its span: two shedding regimes (oblique, normal) and two non-shedding regimes. The occurrence of these wake regimes depended on the curvature, aspect ratio and Reynolds number. In some cases, vortex shedding was entirely suppressed, particularly at higher curvatures. In the laminar wake regime, increasing the curvature or decreasing the aspect ratio restricts vortex shedding to smaller regions along the span of the cylinder. Furthermore, the local angle of incidence where vortex shedding occurs is self-similar across cylinders of the same aspect ratio and varying curvature. After the wake transitions to turbulence, the vortex shedding extends along most of the cylinder span. The difference in the wakes between the concave and convex orientations is attributed to the spanwise flow induced by the finite end conditions, which reduces the generation of spanwise vorticity and increases the incidence of non-shedding and obliquely shedding wakes for the concave cylinder.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 12
- Cited by

