Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T15:38:01.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow structure on a simultaneously pitching and rotating wing

Published online by Cambridge University Press:  02 September 2014

M. Bross  and
D. Rockwell
M. Bross
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
D. Rockwell*
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
*
†Email address for correspondence: dor0@lehigh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A technique of particle image velocimetry is employed to characterize the three-dimensional flow structure on a wing subjected to simultaneous pitch-up and rotational motions. Distinctive vortical structures arise, relative to the well-known patterns on a wing undergoing either pure pitch-up or pure rotation. The features associated with these simultaneous motions include: stabilization of the large-scale vortex generated at the leading edge, which, for pure pitch-up motion, rapidly departs from the leading-edge region; preservation of the coherent vortex system involving both the tip vortex and the leading-edge vortex (LEV), which is severely degraded for pure rotational motion; and rapid relaxation of the flow structure upon termination of the pitch-up component, whereby the relaxed flow converges to a similar state irrespective of the pitch rate. 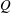Three-dimensional surfaces of iso-$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{Q}$ and helicity are employed in conjunction with sectional representations of spanwise vorticity, velocity and vorticity flux to interpret the flow physics.

JFM classification

Aerodynamics: Aerodynamics Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 354 - 383
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2010 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Ansari, S. A., Phillips, N., Stabler, G., Wilkins, P. C., Zbikowski, R. & Knowles, K. 2009 The effect of advance ratio on the aerodynamics of revolving wings. Exp. Fluids 46, 777–798; and Erratum Exp. Fluids 51, 2011, 571–572.CrossRefGoogle Scholar
Bross, M., Ozen, C. A. & Rockwell, D. 2013 Flow structure on a rotating wing: effect of steady incident flow. Phys. Fluids 25.CrossRefGoogle Scholar
Carr, Z., Chen, C. & Ringuette, M. J. 2013 Finite-span rotating wings: three-dimensional vortex formation and variations with aspect ratio. Exp. Fluids 54, 1444–1470.Google Scholar
Cheng, B., Sane, S. P., Barbera, G., Troolin, D. R., Strand, T. & Deng, X. 2013 Three-dimensional flow visualization and vorticity dynamics in revolving wings. Exp. Fluids 54, 1423–1425.Google Scholar
Dickson, W. B. & Dickinson, M. H. 2004 The effect of advance ratio on the aerodynamics of revolving wings. J. Expl Biol. 207, 4269–4281.Google Scholar
Ekaterinaris, J. & Platzer, M. 1998 Computational predictions of airfoil dynamic stall. Prog. Aerosp. Sci. 33, 759–846.Google Scholar
Eldredge, J. D. & Wang, C.2010 High-fidelity simulations and low-order modeling of a rapidly pitching plate. AIAA Paper 2010-4281.CrossRefGoogle Scholar
Ellington, C. P., van der Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 19–26.Google Scholar
Garmann, D. J. & Visbal, M. R. 2011 Numerical investigation of transitional flow over a rapidly pitching plate. Phys. Fluids 23, 094106.CrossRefGoogle Scholar
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 686, 451–483.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013 Three-dimensional flow structure and aerodynamic loading on revolving wing. Phys. Fluids 25, 034101.Google Scholar
Granlund, K., Ol, M. & Bernal, L.2011 Experiments on pitching plates: force and flowfield measurements at low Reynolds number. AIAA Paper 2011-872.Google Scholar
Hartloper, C., Kinzel, M. & Rival, D. E. 2013 On the competition between leading-edge and tip-vortex growth for a pitching plant. Exp. Fluids 54, 1447–1458.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, vol. 2, pp. 193–208.Google Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49, 329–339.Google Scholar
Lawson, N. J. & Wu, J. 1997 Three-dimensional particle image velocimetry: error analysis of stereoscopic techniques. Meas. Sci. Technol. 8, 897–900.Google Scholar
Le, T. B., Borazjani, I., Kang, S. & Sotiropoulos, F. 2011 On the structure of vortex rings from inclined nozzles. J. Fluid Mech. 686, 451–483.Google Scholar
Lehmann, F. O. & Dickinson, M. H. 1998 The control of wing kinematic and flight forces in fruit flies. J. Expl Biol. 401, 385–401.Google Scholar
Lentink, D. & Dickinson, M. H. 2009a Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Expl Biol. 212, 2691–2704.Google Scholar
Lentink, D. & Dickinson, M. H. 2009b Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.Google Scholar
McCroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14, 285–311.CrossRefGoogle Scholar
Moffatt, H. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Ozen, C. A. & Rockwell, D. 2011 Flow structure on a rotating plate. Exp. Fluids 52, 207–223.Google Scholar
Ozen, C. A. & Rockwell, D. 2012 Three-dimensional vortex structure on a rotating wing. J. Fluid Mech. 748, 932–956.Google Scholar
Poelma, C., Dickson, W. B. & Dickinson, M. H. 2006 Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Exp. Fluids 41, 213–225.Google Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206, 4191–4208.Google Scholar
Shih, C., Lourenco, L., Van Dommelen, L. & Krothapalli, A. 1992 High-fidelity simulations and low-order modeling of a rapidly pitching plate. AIAA J. 30, 1153–1161.Google Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C.-K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46, 284–327.Google Scholar
Visbal, M. R.2011 Three-dimensional flow structure on a heaving low-aspect-ratio wing. AIAA Paper 2011-219.CrossRefGoogle Scholar
Visbal, M. R.2012 Flow structure and unsteady loading over a pitching and perching low-aspect-ratio wing. AIAA Paper 2012-3279.Google Scholar
Visbal, M. R. & Shang, J. S. 1989 Investigations of the flow structure around a rapidly pitching airfoill. AIAA J. 27, 1044–1051.Google Scholar
Wilkins, P. & Knowles, K.2007 Investigation of aerodynamics relevant to flapping-wing micro air vehicles. AIAA Paper 2007-4338.Google Scholar
Wojcik, C. J. & Buchholz, J. H. 2014 Parameter variation and the leading-edge vortex of a rotating flat plate. AIAA J. 52, 348–357.Google Scholar
Yilmaz, T. O.2011 Investigation of three-dimensional flow structure on maneuvering finite-span wings. PhD thesis, Lehigh University.CrossRefGoogle Scholar
Yilmaz, T., Ol, M. & Rockwell, D. 2010 Scaling of flow separation on a pitching low aspect ratio plate. J. Fluids Struct. 26, 1034–1041.Google Scholar
Yilmaz, T. O. & Rockwell, D. 2012 Flow structure on finite-span wings due to pitch-up motion. J. Fluid Mech. 691, 518–545.Google Scholar
Zhang, X. & Schluter, J. U. 2012 Numerical study of the influence of the Reynolds-number on the lift created by a leading edge vortex. Phys. Fluids 24, 065102.Google Scholar