Article contents
Fluid density effects in supersonic jet-induced cratering in a granular bed on a planetary body having an atmosphere in the continuum regime
Published online by Cambridge University Press: 11 March 2021
Abstract
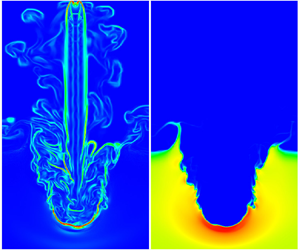
To investigate the effect of atmospheric density and jet-fluid density during supersonic jet-induced cratering on a granular particle bed, large eddy simulation (LES) for the fluid phase coupled with a granular flow model based on kinetic theory is used. Coupling accounts for momentum and energy interaction between particles and fluid. Several simulations are conducted that enable discriminating between the crater characteristics which depend on the atmospheric (or jet) density, and those which depend on the ratio between jet-fluid density and atmospheric density. The crater cross-sectional shapes are controlled by the density ratio between jet fluid and atmosphere. For large such ratios, the craters have a parabolic cross-section shape, are relatively shallow, have large diameters and have subdued ejecta. In contrast, for ratios close to unity, the craters have a conical cross-section, are relatively deep, have relatively small diameters and have substantial ejecta; these craters also display ripples on their walls. The physics leading to these differences is explained. Considerations of particle momentum flux indicate that at same fraction of the crater depth and same radial distance from the jet axis, the radial and vertical components have larger magnitudes for conical craters than for parabolic craters. The spatial distribution of the ratio between the drag force and the force due to the particles resistance to compaction are compared and it is found to be dependent on the jet-to-atmospheric fluid density ratio. A few features of the crater, in particular its depth, only depend on the atmospheric (or jet) fluid density.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 20
- Cited by


