Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T04:04:13.280Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid invasion of an unsaturated leaky porous layer

Published online by Cambridge University Press:  21 July 2015

Samuel S. Pegler ,
Emily L. Bain ,
Herbert E. Huppert  and
Jerome A. Neufeld
Samuel S. Pegler*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Cambridge CB3 0WA, UK Queens’ College, University of Cambridge, Cambridge CB3 9ET, UK
Emily L. Bain
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Cambridge CB3 0WA, UK
Herbert E. Huppert
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Cambridge CB3 0WA, UK Faculty of Science, University of Bristol, Bristol BS8 1UH, UK School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Department of Earth Sciences, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: ssp23@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the flow and leakage of gravity currents injected into an unsaturated (dry), vertically confined porous layer containing a localized outlet or leakage point in its lower boundary. The leakage is driven by the combination of the gravitational hydrostatic pressure head of the current above the outlet and the pressure build-up from driving fluid downstream of the leakage point. Model solutions illustrate transitions towards one of three long-term regimes of flow, depending on the value of a dimensionless parameter 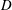$D$, which, when positive, represents the ratio of the hydrostatic head above the outlet for which gravity-driven leakage balances the input flux, to the depth of the medium. If 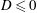$D\leqslant 0$, the input flux is insufficient to accumulate any fluid above the outlet and fluid migrates directly through the leakage pathway. If 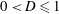$0<D\leqslant 1$, some fluid propagates downstream of the outlet but retains a free surface above it. The leakage rate subsequently approaches the input flux asymptotically but much more gradually than if 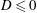$D\leqslant 0$. If 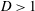$D>1$, the current fills the entire depth of the medium above the outlet. Confinement then fixes gravity-driven leakage at a constant rate but introduces a new force driving leakage in the form of the pressure build-up associated with mobilizing fluid downstream of the outlet. This causes the leakage rate to approach the injection rate faster than would occur in the absence of the confining boundary. This conclusion is in complete contrast to fluid-saturated media, where confinement can potentially reduce long-term leakage by orders of magnitude. Data from a new series of laboratory experiments confirm these predictions.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 777 , 25 August 2015 , pp. 97 - 121
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected $\text{CO}_{2}$ at the Sleipner field, North Sea. J. Geophys. Res. 117, B03309.Google Scholar
Dake, L. P. 2010 Fundamentals of Reservoir Engineering. Elsevier.Google Scholar
Farcas, A. & Woods, A. W. 2007 On the extraction of gas from multilayered rock. J. Fluid Mech. 581, 79–95.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. Jr. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.CrossRefGoogle Scholar
Hesse, M. A. & Woods, A. W. 2010 Buoyant dispersal of $\text{CO}_{2}$ during geological storage. Geophys. Res. Lett. 37, L01403.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Kresic, N. & Stevanovic, Z.(Eds) 2010 Groundwater Hydrology of Springs: Engineering, Theory, Management, and Sustainability. Elsevier.Google Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.Google Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 1. A localized sink. J. Fluid Mech. 666, 391–413.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.CrossRefGoogle Scholar
Orr, F. M. Jr. 2009 Onshore geological storage of CO2 . Science 325, 1656–1658.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014a Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620.CrossRefGoogle Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014b Fluid migration between confined aquifers. J. Fluid Mech. 757, 330–353.CrossRefGoogle Scholar
Pegler, S. S., Kowal, K. N., Hasenclever, L. Q. & Worster, M. G. 2013 Lateral controls on grounding-line dynamics. J. Fluid Mech. 722, R1.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.CrossRefGoogle Scholar
Pritchard, D., Woods, A. W. & Hogg, A. J. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444, 23–47.Google Scholar
Vella, D., Neufeld, J. A., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 2. A line sink. J. Fluid Mech. 666, 414–427.Google Scholar
Zheng, Z., Soh, B., Huppert, H. E. & Stone, H. A. 2013 Fluid drainage from the edge of a porous reservoir. J. Fluid Mech. 718, 558–568.Google Scholar

Pegler et al. supplementary movie

Movie of experiment (c), illustrating the propagation of glycerine (dyed blue) in a leaky porous medium.

Download Pegler et al. supplementary movie(Video)
Video 15.6 MB

Pegler et al. supplementary movie

Movie of experiment (c), illustrating the propagation of glycerine (dyed blue) in a leaky porous medium.

Download Pegler et al. supplementary movie(Video)
Video 5.1 MB