Article contents
Fluid transport in geological reservoirs with background flow
Published online by Cambridge University Press: 24 August 2017
Abstract
This paper presents fundamental analysis of the injection and release of fluid into porous media or geological reservoirs saturated by a different fluid undergoing a background flow, and tests the predictions using analogue laboratory experiments. The study reveals new results important for an understanding of the transport of hazardous contaminants through aquifers and the long-term fate of carbon dioxide ( 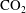 $\text{CO}_{2}$ ) in geological
$\text{CO}_{2}$ ) in geological 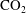 $\text{CO}_{2}$ sequestration. Using numerical and asymptotic analysis, we describe a variety of flow regimes that arise, and demonstrate an almost instantaneous control of injected fluid by the far field conditions in geological reservoirs. For a continuous input, the flow develops a horizontal interface between the injected and ambient fluids. The background flow thereby effectively caps the height of the injected fluid into a shallower region of vertical confinement. For a released parcel of fluid, gravitational spreading is found to become negligible after a short time. A dominant control of the interface by the background pressure gradient arises, and stems from the different velocities at which it drives the injected and ambient fluids individually. Similarity solutions describing these dynamics show that the parcel approaches a slender triangular profile that grows horizontally as
$\text{CO}_{2}$ sequestration. Using numerical and asymptotic analysis, we describe a variety of flow regimes that arise, and demonstrate an almost instantaneous control of injected fluid by the far field conditions in geological reservoirs. For a continuous input, the flow develops a horizontal interface between the injected and ambient fluids. The background flow thereby effectively caps the height of the injected fluid into a shallower region of vertical confinement. For a released parcel of fluid, gravitational spreading is found to become negligible after a short time. A dominant control of the interface by the background pressure gradient arises, and stems from the different velocities at which it drives the injected and ambient fluids individually. Similarity solutions describing these dynamics show that the parcel approaches a slender triangular profile that grows horizontally as 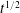 $t^{1/2}$ , where
$t^{1/2}$ , where  $t$ is time, a rate faster than relaxation under gravity. Shock layers develop at the front or back of the parcel, depending on whether it is more or less viscous than the ambient fluid. New analytical results describing the long-term effects of residual trapping due to capillary retention are developed, which yield explicit predictions for the time and length scales on which a parcel of
$t$ is time, a rate faster than relaxation under gravity. Shock layers develop at the front or back of the parcel, depending on whether it is more or less viscous than the ambient fluid. New analytical results describing the long-term effects of residual trapping due to capillary retention are developed, which yield explicit predictions for the time and length scales on which a parcel of  $\text{CO}_{2}$ becomes retained. We end by applying our results to geological contexts, concluding that even slight background motion can have considerable implications for long-term transport through the subsurface.
$\text{CO}_{2}$ becomes retained. We end by applying our results to geological contexts, concluding that even slight background motion can have considerable implications for long-term transport through the subsurface.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 4
- Cited by


