Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-25T19:58:24.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid–structure interactions of a circular cylinder in a stratified fluid

Published online by Cambridge University Press:  25 March 2021

Sarah Christin Open the ORCID record for Sarah Christin [Opens in a new window] ,
Patrice Meunier Open the ORCID record for Patrice Meunier [Opens in a new window]  and
Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]
Sarah Christin*
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France
Patrice Meunier
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France
Stéphane Le Dizès
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France
*
†Email address for correspondence: sarah.christin@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

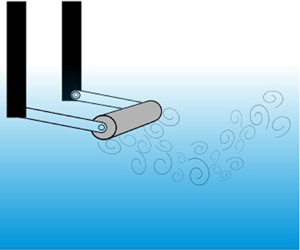
In this article, the objective is to characterize the influence of a continuous stratification on wake-induced vibrations of a circular cylinder. Experimental results are obtained by towing a horizontal cylinder in a horizontal direction perpendicular to its axes, at a constant speed in a linearly stratified fluid made of salty water. The cylinder can move vertically since it is fixed to free-to-rotate arms. The diameter of the cylinder, the length of the arms and the translating speed are varied. Two flow-induced vibrations modes are observed. The first one is analogous to a vortex-induced vibration (VIV) mode: it is associated with a resonance between the vortex shedding frequency and its frequency is proportional to the natural frequency of the mechanical system, as can be predicted by the VIV theory generalized to low mass ratios. Large amplitude oscillations of the cylinder are found to occur in a large range of velocities also in agreement with the low-mass-ratio VIV theory. The second mode is interpreted as a galloping mode. It has a low frequency and a large amplitude, and occurs for low Froude numbers and long arms. It corresponds to the regimes when the buoyancy forces are larger than the inertial and vertical drag forces. By computing the forces on the cylinder, it is shown that stratification is the source of a destabilizing lift when the cylinder departs from its horizontal motion. Only a weak effect of the Reynolds number on the stability characteristics has been observed in the considered range ($500 < Re < 15\,000$).

JFM classification

Geophysical and Geological Flows: Stratified flows Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A97
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Assi, G.R.S., Bearman, P.W. & Meneghini, J.R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.CrossRefGoogle Scholar
Bearman, P.W., Downie, M.J., Graham, J.M.R. & Obasaju, E.D. 1985 Forces on cylinders in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 154, 337–356.CrossRefGoogle Scholar
Bearman, P.W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.CrossRefGoogle Scholar
Bernitsas, M.M., Raghavan, K., Ben-Simon, Y. & Garcia, E.M.H. 2008 VIVACE (Vortex induced vibration aquatic clean energy): a new concept in generation of clean and renewable energy from fluid flow. Trans. ASME: J. Offshore Mech. Arctic Engng 130 (4), 041101.Google Scholar
Bishop, R.E.D. & Hassan, A.Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277 (1368), 51–75.Google Scholar
Blevins, R.D. 1977 Flow-Induced Vibration. Van Nostrand Reinhold Co. p. 377.Google Scholar
Blevins, R.D. 1984 Applied Fluid Dynamics Handbook. Van Nostrand Reinhold.Google Scholar
Bokaian, A.R. & Geoola, F. 1984 Hydroelastic instabilities of square cylinders. J. Sound Vib. 92 (1), 117–141.CrossRefGoogle Scholar
Bosco, M. 2015 Etude du sillage stratifié d'un cylindre. PhD thesis, Aix-Marseille.Google Scholar
Bougeault, P. & Sadourny, R. 2001 Dynamique de l'atmosphère et de l'océan. Editions Ecole Polytechnique.Google Scholar
Boyer, D.L., Davies, P.A., Fernando, H.J.S. & Zhang, X. 1989 Linearly stratified flow past a horizontal circular cylinder. Phil. Trans. R. Soc. Lond. A 328 (1601), 501–528.Google Scholar
Browand, F.K. & Winant, C.D. 1972 Blocking ahead of a cylinder moving in a stratified fluid: an experiment. Geophys. Fluid Dyn. 4 (1), 29–53.CrossRefGoogle Scholar
Capet, A., Stanev, E., Beckers, J.-M., Murray, J. & Grégoire, M. 2016 Decline of the black sea oxygen inventory. Biogeosciences 13, 1287–1297.CrossRefGoogle Scholar
Chang, C.-C.J., Kumar, R.A. & Bernitsas, M.M. 2011 VIV and galloping of single circular cylinder with surface roughness at $3.0\times 10^4 \leqslant Re \leqslant 1.2\times 10^5$. Ocean Engng 38 (16), 1713–1732.CrossRefGoogle Scholar
Chashechkin, Y.D. & Voyekov, I.V. 1993 Vortex systems past a cylinder in a continuously stratified fluid. Izv. Atmos. Ocean. Phys. 29, 787–787.Google Scholar
Coutanceau, M. & Bouard, R. 1977 Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 79 (2), 231–256.CrossRefGoogle Scholar
De Wilde, J.J., Huijsmans, H.M. & Triantafyllou, M.S. 2003 Experimental investigation of the sensitivity to in-line motions and magnus-like lift production on the vortex-induced vibrations. In The Thirteenth International Offshore and Polar Engineering Conference, pp. 593–598. International Society of Offshore and Polar Engineers.Google Scholar
Den Hartog, J.P. 1932 Transmission line vibration due to sleet. Trans. Am. Inst. Elect. Engrs 51 (4), 1074–1076.CrossRefGoogle Scholar
Den Hartog, J.P. 1954 Recent technical manifestations of Von Kármán's vortex wake. Proc. Natl Acad. Sci. USA 40 (3), 155.CrossRefGoogle Scholar
Feng, C.C. 1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and d-section cylinders. PhD thesis, University of British Columbia.Google Scholar
Govardhan, R. & Williamson, C.H.K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Graebel, W.P. 1969 On the slow motion of bodies in stratified and rotating fluids. Q. J. Mech. Appl. Maths 22 (1), 39–54.CrossRefGoogle Scholar
Griffin, O.M. 1985 Vortex-induced vibrations of marine cables and structures. Tech. Rep. 5600. Naval Research Lab., Washington D.C.Google Scholar
Grouthier, C., Michelin, S., Bourguet, R., Modarres-Sadeghi, Y. & De Langre, E. 2014 On the efficiency of energy harvesting using vortex-induced vibrations of cables. J. Fluids Struct. 49, 427–440.CrossRefGoogle Scholar
Guilmineau, E. & Queutey, P. 2002 A numerical simulation of vortex shedding from an oscillating circular cylinder. J. Fluids Struct. 16 (6), 773–794.CrossRefGoogle Scholar
Honji, H. 1988 Vortex motions in stratified wake flows. Fluid. Dyn. Res. 3 (1–4), 425.CrossRefGoogle Scholar
Hwang, R.R. & Lin, S.H. 1992 On laminar wakes behind a circular cylinder in stratified fluids. J. Fluids Engng 114 (1), 20–28.CrossRefGoogle Scholar
Khalak, A & Williamson, C.H.K. 1996 Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 10 (5), 455–472.CrossRefGoogle Scholar
Khalak, A. & Williamson, C.H.K. 1997 Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Engng Ind. Aerodyn. 69, 341–350.CrossRefGoogle Scholar
Khalak, A. & Williamson, C.H.K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.CrossRefGoogle Scholar
Lienhard, J.H. 1966 Synopsis of lift, drag, and vortex frequency data for rigid circular cylinders, vol. 300. Technical Extension Service, Washington State University Pullman, WA.Google Scholar
Lin, J.-T. & Pao, Y.-H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11 (1), 317–338.CrossRefGoogle Scholar
Mannini, C., Marra, A.M. & Bartoli, G. 2014 VIV–galloping instability of rectangular cylinders: review and new experiments. J. Wind Engng Ind. Aerodyn. 132, 109–124.CrossRefGoogle Scholar
Mannini, C., Marra, A.M., Massai, T. & Bartoli, G. 2016 Interference of vortex-induced vibration and transverse galloping for a rectangular cylinder. J. Fluids Struct. 66, 403–423.CrossRefGoogle Scholar
Meunier, P. 2012 Stratified wake of a tilted cylinder. Part 1. Suppression of a von Kármán vortex street. J. Fluid Mech. 699, 174–197.CrossRefGoogle Scholar
Munk, W.H. 1966 Abyssal recipes. In Deep Sea Research and Oceanographic Abstracts, vol. 13, pp. 707–730. Citeseer.CrossRefGoogle Scholar
Nakamura, Y., Hirata, K. & Kashima, K. 1994 Galloping of a circular cylinder in the presence of a splitter plate. J. Fluids Struct. 8 (4), 355–365.CrossRefGoogle Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.CrossRefGoogle Scholar
Ohya, Y., Uchida, T. & Nagai, T. 2013 Near wake of a horizontal circular cylinder in stably stratified flows. Open J. Fluid Dyn. 3, 311–320.CrossRefGoogle Scholar
Parkinson, G.V. & Wawzonek, M.A. 1981 Some considerations of combined effects of galloping and vortex resonance. J. Wind Engng Ind. Aerodyn. 8 (1–2), 135–143.CrossRefGoogle Scholar
Placzek, A., Sigrist, J.-F. & Hamdouni, A. 2009 Numerical simulation of an oscillating cylinder in a cross-flow at low Reynolds number: forced and free oscillations. Comput. Fluids 38 (1), 80–100.CrossRefGoogle Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.CrossRefGoogle Scholar
Sarpkaya, T. 1978 Fluid forces on oscillating cylinders. STIA 104, 275–290.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Song, R., Shan, X., Lv, F. & Xie, T. 2015 A study of vortex-induced energy harvesting from water using PZT piezoelectric cantilever with cylindrical extension. Ceram. Intl 41, S768–S773.CrossRefGoogle Scholar
Strouhal, V. 1878 Über eine besondere art der tonerregung. Ann. Phys. 241 (10), 216–251.CrossRefGoogle Scholar
Tritton, D.J. 2012 Physical Fluid Dynamics. Springer Science & Business Media.Google Scholar
Von Karman, T. 1911 Über den mechanismus des widerstandes, den ein bewegter körper in einer flüssigkeit erfährt. Nachr. Ges. Wiss. Göttingen 1911, 509–517.Google Scholar
von Wieselsberger, C. 1921 Neuere feststellungen uber die gesetze des flussigkeits und luftwiderstands. Phys. Z. 22, 321.Google Scholar
Williamson, C.H.K. 1996 a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Williamson, C.H.K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Yamamoto, T. & Nath, J.H. 1976 High Reynolds number oscillating flow by cylinders. Coast. Engng 1 (15), 135.CrossRefGoogle Scholar
Zheng, Z.C. & Zhang, N 2008 Frequency effects on lift and drag for flow past an oscillating cylinder. J. Fluids Struct. 24 (3), 382–399.CrossRefGoogle Scholar