Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T17:34:35.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Flux expulsion with dynamics

Published online by Cambridge University Press:  24 February 2016

Andrew D. Gilbert ,
Joanne Mason  and
Steven M. Tobias
Andrew D. Gilbert
Affiliation:
Department of Mathematics and Computer Science, College of Engineering, Mathematics and Physical Sciences, University of Exeter, EX4 4QF, UK
Joanne Mason*
Affiliation:
Department of Mathematics and Computer Science, College of Engineering, Mathematics and Physical Sciences, University of Exeter, EX4 4QF, UK
Steven M. Tobias
Affiliation:
Department of Applied Mathematics, University of Leeds, LS2 9JT, UK
*
†Email address for correspondence: j.mason@exeter.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In the process of flux expulsion, a magnetic field is expelled from a region of closed streamlines on a 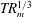$TR_{m}^{1/3}$ time scale, for magnetic Reynolds number 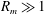$R_{m}\gg 1$ ($T$ being the turnover time of the flow). This classic result applies in the kinematic regime where the flow field is specified independently of the magnetic field. A weak magnetic ‘core’ is left at the centre of a closed region of streamlines, and this decays exponentially on the 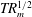$TR_{m}^{1/2}$ time scale. The present paper extends these results to the dynamical regime, where there is competition between the process of flux expulsion and the Lorentz force, which suppresses the differential rotation. This competition is studied using a quasi-linear model in which the flow is constrained to be axisymmetric. The magnetic Prandtl number 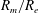$R_{m}/R_{e}$ is taken to be small, with 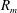$R_{m}$ large, and a range of initial field strengths 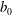$b_{0}$ is considered. Two scaling laws are proposed and confirmed numerically. For initial magnetic fields below the threshold 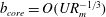$b_{core}=O(UR_{m}^{-1/3})$, flux expulsion operates despite the Lorentz force, cutting through field lines to result in the formation of a central core of magnetic field. Here 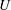$U$ is a velocity scale of the flow and magnetic fields are measured in Alfvén units. For larger initial fields the Lorentz force is dominant and the flow creates Alfvén waves that propagate away. The second threshold is $b_{dynam}=O(UR_{m}^{-3/4})$, below which the field follows the kinematic evolution and decays rapidly. Between these two thresholds the magnetic field is strong enough to suppress differential rotation, leaving a magnetically controlled core spinning in solid body motion, which then decays slowly on a time scale of order 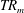$TR_{m}$.

JFM classification

MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Turbulent Flows: Turbulent Flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 568 - 588
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bajer, K. 1998 Flux expulsion by a point vortex. Eur. J. Mech. (B/Fluids) 17, 653–664.Google Scholar
Bajer, K., Bassom, A. P. & Gilbert, A. D. 2001 Accelerated diffusion in the centre of a vortex. J. Fluid Mech. 437, 395–411; Referred to as BBG in the text.CrossRefGoogle Scholar
Bassom, A. P. & Gilbert, A. D. 1997 Nonlinear equilibration of a dynamo in a smooth helical flow. J. Fluid Mech. 343, 375–406.CrossRefGoogle Scholar
Bernoff, A. J. & Lingevitch, J. F. 1994 Rapid relaxation of an axisymmetric vortex. Phys. Fluids 6, 3717–3723.Google Scholar
Cattaneo, F. 1994 On the effects of a weak magnetic field on turbulent transport. Astrophys. J. 434, 200–205.CrossRefGoogle Scholar
Cattaneo, F. & Vainshtein, S. I. 1991 Suppression of turbulent transport by weak magnetic field. Astrophys. J. 376, L21–L24.CrossRefGoogle Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.CrossRefGoogle Scholar
Dritschel, D. G. & Tobias, S. M. 2012 Two-dimensional magnetohydrodynamic turbulence in the small magnetic Prandtl number limit. J. Fluid Mech. 703, 85–98.CrossRefGoogle Scholar
Galloway, D. J., Proctor, M. R. E. & Weiss, N. O. 1978 Magnetic flux ropes and convection. J. Fluid Mech. 87, 243–261.Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012 Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106, 392–428.Google Scholar
Keating, S. R. & Diamond, P. H. 2008 Turbulent resistivity in wavy two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 595, 173–202.Google Scholar
Keating, S. R., Silvers, L. J. & Diamond, P. H. 2008 On cross-phase and the quenching of the turbulent diffusion of magnetic fields in two dimensions. Astrophys. J. 678, L137–L140.Google Scholar
Kim, E.-J. 2006 Consistent theory of turbulent transport in two dimensional magnetohydrodynamics. Phys. Rev. Lett. 96, 084504.CrossRefGoogle ScholarPubMed
Mestel, L. & Weiss, N. O. 1986 Magnetic fields and non-uniform rotation in stellar radiative zones. Mon. Not. R. Astron. Soc. 226, 123–135.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Moffatt, H. K. & Kamkar, H. 1983 The time-scale associated with flux expulsion. In Stellar and Planetary Magnetism (ed. Soward, A. M.), Gordon and Breach.Google Scholar
Olver, F. J. W., Lozier, D. W., Boisvert, R. F. & Clark, C. W. 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Parker, R. L. 1966 Reconnection of lines of force in rotating spheres and cylinders. Proc. R. Soc. Lond. A 291, 60–72.Google Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.Google Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostrophic instability. J. Atmos. Sci. 69, 1633–1656.Google Scholar
Taylor, J. B. 1963 The magnetohydrodynamics of a rotating fluid and the Earth’s dynamo problem. Proc. R. Soc. Lond. A 9, 274–283.Google Scholar
Tobias, S. M. & Cattaneo, F. 2008 Limited role of spectra in dynamo theory: coherent versus random dynamos. Phys. Rev. Lett. 101, 125003.Google Scholar
Tobias, S. M., Dagon, K. & Marston, J. B. 2011 Astrophysical fluid dynamics via direct statistical simulation. Astrophys. J. 727, 127–138.Google Scholar
Vainshtein, S. I. & Cattaneo, F. 1992 Nonlinear restrictions on dynamo action. Astrophys. J. 393, 165–171.Google Scholar
Weiss, N. O. 1966 The expulsion of magnetic flux by eddies. Proc. R. Soc. Lond. A 293, 310–328.Google Scholar
Weiss, N. O. & Proctor, M. R. E. 2014 Magnetoconvection. Cambridge University Press.Google Scholar