Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:17:14.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractal-like actuator disc theory for optimal energy extraction

Published online by Cambridge University Press:  30 September 2021

D. Dehtyriov Open the ORCID record for D. Dehtyriov [Opens in a new window] ,
A.M. Schnabl ,
C.R. Vogel Open the ORCID record for C.R. Vogel [Opens in a new window] ,
S. Draper Open the ORCID record for S. Draper [Opens in a new window] ,
T.A.A. Adcock Open the ORCID record for T.A.A. Adcock [Opens in a new window]  and
R.H.J. Willden
D. Dehtyriov*
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
A.M. Schnabl
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
C.R. Vogel
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
S. Draper
Affiliation:
Oceans Graduate School, University of Western Australia, Perth 6009, Australia
T.A.A. Adcock
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
R.H.J. Willden
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
*
†Email address for correspondence: daniel.dehtyriov@eng.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

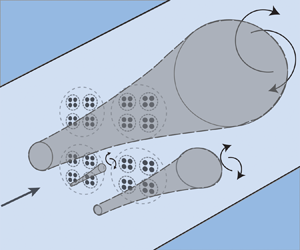
The limit of power extraction by a device which makes use of constructive interference, i.e. local blockage, is investigated theoretically. The device is modelled using actuator disc theory in which we allow the device to be split into arrays and these then into sub-arrays an arbitrary number of times so as to construct an $n$-level multi-scale device in which the original device undergoes $n-1$ sub-divisions. The alternative physical interpretation of the problem is a planar system of arrayed turbines in which groups of turbines are homogeneously arrayed at the smallest $n\mathrm {th}$ scale, and then these groups are homogeneously spaced relative to each other at the next smallest $n-1\mathrm {th}$ scale, with this pattern repeating at all subsequent larger scales. The scale-separation idea of Nishino & Willden (J. Fluid. Mech., vol. 708, 2012b, pp. 596–606) is employed, which assumes mixing within a sub-array occurs faster than mixing of the by-pass flow around that sub-array, so that in the $n$-scale device mixing occurs from the inner scale to the outermost scale in that order. We investigate the behaviour of an arbitrary level multi-scale device, and determine the arrangement of actuator discs ($n\mathrm {th}$ level devices) which maximises the power coefficient (ratio of power extracted to undisturbed kinetic energy flux through the net disc frontal area). We find that this optimal arrangement is close to fractal, and fractal arrangements give similar results. With the device placed in an infinitely wide channel, i.e. zero global blockage, we find that the optimum power coefficient tends to unity as the number of device scales tends to infinity, a 27/16 increase over the Lanchester–Betz limit of $0.593$. For devices in finite width channels, i.e. non-zero global blockage, similar observations can be made with further uplift in the maximum power coefficient. We discuss the fluid mechanics of this energy extraction process and examine the scale distribution of thrust and wake velocity coefficients. Numerical demonstration of performance uplift due to multi-scale dynamics is also provided. We demonstrate that bypass flow remixing and ensuing energy losses increase the device power coefficient above the limits for single devices, so that although the power coefficient can be made to increase, this is at the expense of the overall efficiency of energy extraction which decreases as wake-scale remixing losses necessarily rise. For multi-scale devices in finite overall blockage two effects act to increase extractable power; an overall streamwise pressure gradient associated with finite blockage, and wake pressure recoveries associated with bypass-scale remixing.

JFM classification

Geophysical and Geological Flows: Coastal engineering Waves/Free-surface Flows: Channel flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A40
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adcock, T.A.A., Draper, S., Willden, R.H.J. & Vogel, C.R. 2021 The fluid mechanics of tidal stream energy conversion. Annu. Rev. Fluid Mech. 53 (1), 287–310.CrossRefGoogle Scholar
Betz, A. 1920 Das Maximum der theoretisch möglichen Ausnützung des Windes durch Windmotoren. Zeitschrift für das gesamte Turbinenwesen 26, 307–309.Google Scholar
Bleeg, J., Purcell, M., Ruisi, R. & Traiger, E. 2018 Wind farm blockage and the consequences of neglecting its impact on energy production. Energies 11 (6), 1609.CrossRefGoogle Scholar
Byrd, R.H., Hribar, M.E. & Nocedal, J. 1999 An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 9 (4), 877–900.CrossRefGoogle Scholar
Cooke, S.C, Willden, R.H.J., Byrne, B., Stallard, T. & Olczak, A. 2015 Experimental investigation of tidal turbine partial array theory using porous discs. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France.Google Scholar
Cooke, S.C., Willden, R.H.J. & Byrne, B.W. 2016 The potential of cross-stream aligned sub-arrays to increase tidal turbine efficiency. Renew. Energy (ed. C.G. Soares), 97, 284–292. CRC.CrossRefGoogle Scholar
Draper, S. & Nishino, T. 2014 Centred and staggered arrangements of tidal turbines. J. Fluid Mech. 739, 72–93.CrossRefGoogle Scholar
Garrett, C. & Cummins, P. 2007 The efficiency of a turbine in a tidal channel. J. Fluid Mech. 588, 243–251.CrossRefGoogle Scholar
Glauert, H. 1926 The Elements of Aerofoil and Airscrew Theory. Cambridge University Press.Google Scholar
Hunter, W., Nishino, T. & Willden, R.H.J. 2015 Investigation of tidal turbine array tuning using 3D Reynolds-averaged Navier–Stokes simulations. Intl J. Mar. Energy 10, 39–51.CrossRefGoogle Scholar
Joukowsky, N.E. 1920 Windmill of the NEJ type. In Transactions of the Central Institute for Aero-Hydrodynamics of Moscow.Google Scholar
Lanchester, F.W. 1915 A contribution to the theory of propulsion and the screw propeller. J. Am. Soc. Nav. Engrs 27 (2), 509–510.Google Scholar
Launder, B.E. & Spalding, D.B. 1974 The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. Engng 3 (2), 269–289.CrossRefGoogle Scholar
McNaugton, J., Cao, B., Vogel, C.R. & Willden, R.H.J. 2019 Model scale testing of multi-rotor arrays designed to exploit constructive interference effects. In Technical Committee of the European Wave and Tidal Energy Conference.Google Scholar
Nishino, T. & Willden, R.H.J. 2012 a Effects of 3-D channel blockage and turbulent wake mixing on the limit of power extraction by tidal turbines. Intl J. Heat Fluid Flow 37, 123–135.CrossRefGoogle Scholar
Nishino, T. & Willden, R.H.J. 2012 b The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 708, 596–606.CrossRefGoogle Scholar
Nishino, T. & Willden, R.H.J. 2013 Two-scale dynamics of flow past a partial cross-stream array of tidal turbines. J. Fluid Mech. 730, 220–244.CrossRefGoogle Scholar
Ugray, Z., Lasdon, L., Plummer, J., Glover, F., Kelly, J. & Marti, R. 2007 Scatter search and local NLP solvers: a multistart framework for global optimization. INFORMS J. Comput. 19 (3), 328–340.CrossRefGoogle Scholar
Vennell, R. 2010 Tuning turbines in a tidal channel. J. Fluid Mech. 663, 253–267.CrossRefGoogle Scholar
Vennell, R. 2011 Tuning tidal turbines in-concert to maximise farm efficiency. J. Fluid Mech. 671, 587–604.CrossRefGoogle Scholar
Vennell, R. 2013 Exceeding the Betz limit with tidal turbines. Renew. Energy 55, 277–285.CrossRefGoogle Scholar
Vogel, C.R., Houlsby, G.T. & Willden, R.H.J. 2016 Effect of free surface deformation on the extractable power of a finite width turbine array. Renew. Energy 88, 317–324.CrossRefGoogle Scholar
Vogel, C.R., Willden, R.H.J. & Houlsby, G.T. 2018 Blade element momentum theory for a tidal turbine. Ocean Engng 169, 215–226.CrossRefGoogle Scholar
Whelan, J.I., Graham, J.M.R. & Peiró, J. 2009 A free-surface and blockage correction for tidal turbines. J. Fluid Mech. 624, 281–291.CrossRefGoogle Scholar