Article contents
Freak wave in a two-dimensional directional wavefield with bottom topography change. Part 1. Normal incidence wave
Published online by Cambridge University Press: 17 March 2023
Abstract
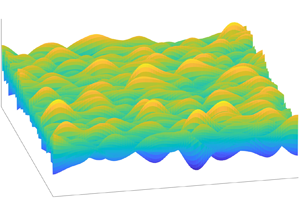
In the propagation and evolution of sea waves, previous studies pointed out that the occurrence of the freak wave height is significantly related to the quasi-resonant four-wave interaction in the modulated waves. From numerical--experimental study over an uneven bottom, the nonlinear effect caused by the bathymetry change also contributes to the occurrence of extreme events in unidirectional waves. To comprehensively analyse the two-dimensional wavefield, this study develops an evolution model for a directional random wavefield based on the depth-modified nonlinear Schrödinger equation, which considers the nonlinear resonant interactions and the wave shoaling the shallow water. Through Monte Carlo simulation, we discuss the directional effect on the four-wave interaction in the wave train and the maximum wave height distribution from deep to shallow water with a slow varying slope. The numerical result indicates that the directional spreading has a dispersion effect on the freak wave height. In a shallow-water environment, this effect becomes weak, and the bottom topography change is the main influencing factor in the wave evolution.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by


