Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T12:55:57.522Z Has data issue: false hasContentIssue false
  • English
  • Français

A freely suspended robotic swimmer propelled by viscoelastic normal stresses

Published online by Cambridge University Press:  28 June 2022

L.A. Kroo Open the ORCID record for L.A. Kroo [Opens in a new window] ,
Jeremy P. Binagia Open the ORCID record for Jeremy P. Binagia [Opens in a new window] ,
Noah Eckman ,
Manu Prakash Open the ORCID record for Manu Prakash [Opens in a new window]  and
Eric S.G. Shaqfeh Open the ORCID record for Eric S.G. Shaqfeh [Opens in a new window]
L.A. Kroo
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, United States
Jeremy P. Binagia
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA 94305, United States
Noah Eckman
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA 94305, United States
Manu Prakash
Affiliation:
Department of Bioengineering, Stanford University, Stanford, CA 94305, United States
Eric S.G. Shaqfeh*
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, United States Department of Chemical Engineering, Stanford University, Stanford, CA 94305, United States
*
†Email address for correspondence: esgs@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

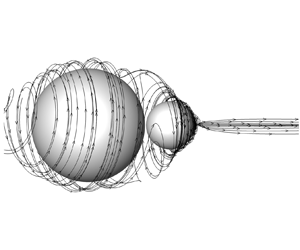
We present a self-propelled axisymmetric low-Reynolds-number swimmer (force- and torque-free) that, while unable to swim in a Newtonian fluid, propels itself in a non-Newtonian fluid as a result of fluid elasticity. The propulsion gait is pure ‘swirling’ and is demonstrated using a robotic swimmer, comprised of a ‘head’ sphere and a ‘tail’ sphere, whose swimming speed is shown to demonstrate good agreement with a microhydrodynamic asymptotic theory and numerical simulations. Schlieren imaging demonstrates that propulsion of the swimmer is driven by a strong viscoelastic jet at the tail, which develops due to the fore–aft asymmetry of the swimmer. Optimized cylindrical and conic tail geometries are shown to double the propulsive signal, relative to the optimal spherical tail. We show that we can use observations of this robot to infer rheological properties of the surrounding fluid. We measure the primary normal stress coefficient $\varPsi _1$ at shear rates ${<}1\,{\rm Hz}$, and show reasonable agreement with extrapolated bench-top measurements ($0.8\unicode{x2013}1.2\,{\rm Pa}\,{\rm s}^2$ difference). We also derive how the head rotation may be used to measure the second normal stress coefficient, $\varPsi _2$. The study demonstrates the exciting potential for a ‘swimming rheometer’, examining the intersection between swimming and sensing in complex fluids.

JFM classification

Biological Fluid Dynamics: Propulsion Non-Newtonian Flows: Rheology Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 944 , 10 August 2022 , A20
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Binagia, J.P., Guido, C.J. & Shaqfeh, E.S.G. 2019 Three-dimensional simulations of undulatory and amoeboid swimmers in viscoelastic fluids. Soft Matt. 15 (24), 4836–4855.10.1039/C8SM02518ECrossRefGoogle ScholarPubMed
Binagia, J.P., Phoa, A., Housiadas, K.D. & Shaqfeh, E.S.G. 2020 Swimming with swirl in a viscoelastic fluid. J. Fluid Mech. 900, A4.CrossRefGoogle Scholar
Binagia, J.P. & Shaqfeh, E.S.G. 2021 Self-propulsion of a freely suspended swimmer by a swirling tail in a viscoelastic fluid. Phys. Rev. Fluids 6 (5), 053301.CrossRefGoogle Scholar
Bird, R.B., Armstrong, R.C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. vol. 1: Fluid Mechanics. John Wiley and Sons Inc., New York, NY.Google Scholar
Boger, D.V. & Walters, K. 2012 Rheological Phenomena in Focus. Elsevier.Google Scholar
Broyden, C.G. 1965 A class of methods for solving nonlinear simultaneous equations. Maths Comput. 19 (92), 577–593.CrossRefGoogle Scholar
Datt, C., Nasouri, B. & Elfring, G.J. 2018 Two-sphere swimmers in viscoelastic fluids. Phys. Rev. Fluids 3 (12), 123301.CrossRefGoogle Scholar
Fattal, R. & Kupferman, R. 2004 Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newtonian Fluid Mech. 123 (2–3), 281–285.CrossRefGoogle Scholar
Ghosh, A., Dasgupta, D., Pal, M., Morozov, K.I., Leshansky, A.M. & Ghosh, A. 2018 Helical nanomachines as mobile viscometers. Adv. Funct. Mater. 28 (25), 1705687.CrossRefGoogle Scholar
Ghosh, A. & Ghosh, A. 2021 Mapping viscoelastic properties using helical magnetic nanopropellers. Trans. Indian Natl Acad. Engng 6 (2), 429–438.CrossRefGoogle Scholar
Ham, F., Mattsson, K. & Iaccarino, G. 2006 Accurate and stable finite volume operators for unstructured flow solvers. In Center for Turbulence Research Annual Research Briefs, pp. 243–261. Center for Turbulence Research, NASA Ames/Stanford University Stanford.Google Scholar
Housiadas, K.D., Binagia, J.P. & Shaqfeh, E.S.G. 2021 Squirmers with swirl at low Weissenberg number. J. Fluid Mech. 911, A16.CrossRefGoogle Scholar
Hulsen, M.A., Fattal, R. & Kupferman, R. 2005 Flow of viscoelastic fluids past a cylinder at high Weissenberg number: stabilized simulations using matrix logarithms. J. Non-Newtonian Fluid Mech. 127 (1), 27–39.CrossRefGoogle Scholar
Keim, N.C., Garcia, M. & Arratia, P.E. 2012 Fluid elasticity can enable propulsion at low Reynolds number. Phys. Fluids 24 (8), 081703.CrossRefGoogle Scholar
Khair, A.S. & Squires, T.M. 2010 Active microrheology: a proposed technique to measure normal stress coefficients of complex fluids. Phys. Rev. Lett. 105 (15), 156001.CrossRefGoogle ScholarPubMed
Kim, S. & Karrila, S.J. 2013 Microhydrodynamics: Principles and Selected Applications. Courier Corporation.Google Scholar
Kraft, D., et al. 1988 A software package for sequential quadratic programming. German Research and Testing Institute for Aerospace.Google Scholar
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Progr. Phys. 72 (9), 096601.10.1088/0034-4885/72/9/096601CrossRefGoogle Scholar
Morrison, F.A., et al. 2001 Understanding Rheology, vol. 1. Oxford University Press.Google Scholar
Oldroyd, J.G. 1950 On the formulation of rheological equations of state. Proc. R. Soc. Lond. A 200 (1063), 523–541.Google Scholar
Padhy, S., Shaqfeh, E.S.G., Iaccarino, G., Morris, J.F. & Tonmukayakul, N. 2013 Simulations of a sphere sedimenting in a viscoelastic fluid with cross shear flow. J. Non-Newtonian Fluid Mech. 197, 48–60.CrossRefGoogle Scholar
Pak, O.S., Zhu, L., Brandt, L. & Lauga, E. 2012 Micropropulsion and microrheology in complex fluids via symmetry breaking. Phys. Fluids 24 (10), 103102.10.1063/1.4758811CrossRefGoogle Scholar
Puente-Velázquez, J.A., Godínez, F.A., Lauga, E. & Zenit, R. 2019 Viscoelastic propulsion of a rotating dumbbell. Microfluid. Nanofluid. 23 (9), 108.CrossRefGoogle Scholar
Purcell, E.M. 1977 Life at low Reynolds number. Am. J. Phys. 45 (1), 3–11.CrossRefGoogle Scholar
Qiu, T., Lee, T.-C., Mark, A.G., Morozov, K.I., Münster, R., Mierka, O., Turek, S., Leshansky, A.M. & Fischer, P. 2014 Swimming by reciprocal motion at low Reynolds number. Nat. Commun. 5 (1), 5119.10.1038/ncomms6119CrossRefGoogle ScholarPubMed
Richter, D., Iaccarino, G. & Shaqfeh, E.S.G. 2010 Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers. J. Fluid Mech. 651, 415–442.CrossRefGoogle Scholar
Rogowski, L.W., Ali, J., Zhang, X., Wilking, J.N., Fu, H.C. & Kim, M.J. 2021 Symmetry breaking propulsion of magnetic microspheres in nonlinearly viscoelastic fluids. Nat. Commun. 12 (1), 1116.CrossRefGoogle ScholarPubMed
Saadat, A., Guido, C.J., Iaccarino, G. & Shaqfeh, E.S.G. 2018 Immersed-finite-element method for deformable particle suspensions in viscous and viscoelastic media. Phys. Rev. E 98 (6), 063316.CrossRefGoogle Scholar
Walters, K. & Waters, N.D. 1963 On the use of a rotating sphere in the measurement of elastico-viscous parameters. Br. J. Appl. Phys. 14 (10), 667.10.1088/0508-3443/14/10/316CrossRefGoogle Scholar
Walters, K. & Waters, N.D. 1964 a The interpretation of experimental results obtained from a rotating-sphere elastoviscometer. Br. J. Appl. Phys. 15 (8), 989.CrossRefGoogle Scholar
Walters, K. & Waters, N.D. 1964 b The steady flow of a Rivlin–Ericksen fluid induced by a rotating-sphere. Rheol. Acta 3 (4), 312–315.10.1007/BF02096168CrossRefGoogle Scholar
Yang, M., Krishnan, S. & Shaqfeh, E.S.G. 2016 Numerical simulations of the rheology of suspensions of rigid spheres at low volume fraction in a viscoelastic fluid under shear. J. Non-Newtonian Fluid Mech. 233, 181–197.CrossRefGoogle Scholar

Kroo et al. supplementary movie 1

Schlieren imaging of a propelling swirler, demonstrating a non-inertial, viscoelastic jet coming off the tail (to the left). The counter-rotating head is on the right, and the robot propels to the right. 8x playback speed.

Download Kroo et al. supplementary movie 1(Video)
Video 8.3 MB

Kroo et al. supplementary movie 2

A torque-free, robotic swimmer self-propelling at low Re in the direction of the "head" sphere, in a viscoelastic polymeric fluid (0.1% polyacrylamide-based Boger fluid).

Download Kroo et al. supplementary movie 2(Video)
Video 7.4 MB

Kroo et al. supplementary movie 3

Swimmer does not propel in Newtonian fluids at low Re. This movie depicts the swimmer failing to propel in pure corn syrup (control experiment).

Download Kroo et al. supplementary movie 3(Video)
Video 8.9 MB