Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T21:00:04.347Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-stream coherent structures in growing boundary layers: a link to near-wall streaks

Published online by Cambridge University Press:  05 August 2015

Kengo Deguchi  and
Philip Hall
Kengo Deguchi
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Philip Hall*
Affiliation:
School of Mathematics, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: phil.hall@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In a recent paper, Deguchi & Hall (J. Fluid Mech., vol. 752, 2014a, pp. 602–625) described a new kind of exact coherent structure which sits at the edge of an asymptotic suction boundary layer at high values of the Reynolds number 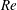$Re$. At a distance 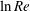$\ln Re$ from the wall, the structure is driven by the fully nonlinear interaction of tiny rolls, waves and streaks convected downstream at almost the free-stream speed. The interaction problem satisfies the unit-Reynolds-number three-dimensional Navier–Stokes equations and is localized in a layer of the same depth as the unperturbed boundary layer. Here, we show that the interaction problem is generic to any boundary layer that approaches its free-stream form through an exponentially small correction. It is shown that away from the layer where it is generated the induced roll–streak flow is dominated by non-parallel effects which now play a major role in the streamwise evolution of the structure. The similarity with the parallel boundary layer case is restricted only to the layer where it is generated. It is shown that non-parallel effects cause the structure to persist only over intervals of finite length in any growing boundary layer and lead to a flow structure reminiscent of turbulent boundary layer simulations. The results found shed light on a possible mechanism to couple near-wall streaks with coherent structures located towards the edge of a turbulent boundary layer. Some discussion of how the mechanism adapts to a three-dimensional base flow is given.

JFM classification

Boundary Layers: Boundary layer stability Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 451 - 484
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary-layer. J. Fluid Mech. 422, 1–54.Google Scholar
Brandt, L., Henningson, D. S. & Ponziani, D. 2002 Weakly nonlinear analysis of boundary layer receptivity of free-stream disturbances. Phys. Fluids 14, 1426–1441.CrossRefGoogle Scholar
Brown, S. N. & Stewartson, K. 1965 On similarity solutions of the boundary-layer equations with algebraic decay. J. Fluid Mech. 23 (4), 673–687.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J.-Ch. & Bottaro, A. 2011 Edge states in a boundary layer. Phys. Fluids 23, 051705.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014a Free-stream coherent structures in parallel boundary layer flows. J. Fluid Mech. 752, 602–625.Google Scholar
Deguchi, K. & Hall, P. 2014b The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Deguchi, K. & Hall, P. 2014c Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. Lond. A 372, 20130352.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.CrossRefGoogle Scholar
Dong, M. & Wu, X. 2013 On continuous spectra of the Orr–Sommerfeld/Squire equations and entrainment of free-stream vortical disturbances. J. Fluid Mech. 732, 616–659.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21, 111701.CrossRefGoogle Scholar
Duguet, Y., Schlatter, P., Henningson, D. S. & Eckhardt, B. 2012 Self-sustained localized structures in a boundary layer flow. Phys. Rev. Lett. 108, 044501.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Goldstein, S. 1965 On backward boundary layers and flow in converging passages. J. Fluid Mech. 21, 33–45.Google Scholar
Gulyaev, A. N., Kozlov, V. E., Kuznetsov, V. R., Mineev, B. I. & Sekundov, A. N. 1989 Interacton of laminar boundary layer with external turbulence. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 6, 700–710.Google Scholar
Halcrow, J., Gibson, J. F., Cvitanović, P. & Viswavath, D. 2009 Heteroclinic connections in plane Couette flow. J. Fluid Mech. 621, 365–376.CrossRefGoogle Scholar
Hall, P. 1982 Taylor–Gor̈tler vortices in fully developed or boundary layer flows: linear theory. J. Fluid Mech. 124, 474–494.Google Scholar
Hall, P. 1983 The linear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 130, 41–58.Google Scholar
Hall, P. 1985 The Görtler vortex mechanism in three-dimensional boundary layers. Proc. R. Soc. Lond. A 399, 135–152.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–337.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Khapko, T., Kreilos, T., Schlatter, P., Duguet, Y., Eckhardt, B. & Henningson, D. S. 2012 Localized edge states in the asymptotic suction boundary layer. J. Fluid Mech. 717, R6.Google Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane Couette flow. Chaos 22, 047505.CrossRefGoogle ScholarPubMed
Kreilos, T., Veble, G., Schneider, T. M. & Eckhardt, B. 2013 Edge states for the turbulent transition in the asymptotic suction boundary layer. J. Fluid Mech. 726, 100–122.Google Scholar
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The ‘bursting’ phenomenon in a turbulent boundary-layer. J. Fluid Mech. 48, 339–352.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary-layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.CrossRefGoogle Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar