Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Fei
Choudhari, Meelan M.
Duan, Lian
and
Chang, Chau-Lyan
2014.
Nonlinear Development and Secondary Instability of Traveling Crossflow Vortices.
Lovig, Erica N.
Downs, Robert S.
and
White, Edward B.
2014.
Passive Laminar Flow Control at Low Turbulence Levels.
AIAA Journal,
Vol. 52,
Issue. 5,
p.
1072.
Li, Fei
Choudhari, Meelan M.
Duan, Lian
and
Chang, Chau-Lyan
2014.
Nonlinear development and secondary instability of traveling crossflow vortices.
Physics of Fluids,
Vol. 26,
Issue. 6,
Mistry, V. I.
Page, G. J.
and
McGuirk, J. J.
2015.
Simulation of Receptivity and Induced Transition From Discrete Roughness Elements.
Flow, Turbulence and Combustion,
Vol. 95,
Issue. 2-3,
p.
301.
Li, Fei
Choudhari, Meelan M.
and
Duan, Lian
2015.
Direct Numerical Simulation of Transition due to Traveling Crossflow Vortices.
Serpieri, Jacopo
and
Kotsonis, Marios
2016.
Three-dimensional organisation of primary and secondary crossflow instability.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
200.
Kuester, Matthew S.
and
White, Edward B.
2016.
Structure of turbulent wedges created by isolated surface roughness.
Experiments in Fluids,
Vol. 57,
Issue. 4,
Serpieri, Jacopo
and
Kotsonis, Marios
2016.
Tomographic PIV investigation of crossflow instability of swept wing boundary layers.
Serpieri, Jacopo
and
Kotsonis, Marios
2016.
Spatio-temporal characteristics of secondary instabilities in swept wing boundary layers.
Serpieri, Jacopo
Yadala Venkata, Srikar
and
Kotsonis, Marios
2017.
Conditioning of cross-flow instability modes using dielectric barrier discharge plasma actuators.
Journal of Fluid Mechanics,
Vol. 833,
Issue. ,
p.
164.
Butler, Adam
and
Wu, Xuesong
2018.
Stationary crossflow vortices near the leading edge of three-dimensional boundary layers: the role of non-parallelism and excitation by surface roughness.
Journal of Fluid Mechanics,
Vol. 845,
Issue. ,
p.
93.
Yadala, Srikar
Hehner, Marc T.
Serpieri, Jacopo
Benard, Nicolas
Dörr, Philipp C.
Kloker, Markus J.
and
Kotsonis, Marios
2018.
Experimental control of swept-wing transition through base-flow modification by plasma actuators.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
Yadala Venkata, Srikar
Hehner, Marc
Serpieri, Jacopo
Benard, Nicolas
and
Kotsonis, Marios
2018.
Swept-Wing Transition Control Using AC-DBD Plasma Actuators.
Guo, Zhengfei
and
Kloker, Markus J.
2019.
Control of crossflow-vortex-induced transition by unsteady control vortices.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
427.
Rizzo, Paolo
Serpieri, Jacopo
and
Kotsonis, Marios
2019.
Crossflow Transition of a Swept-Wing Boundary Layer and its Sensitivity to Free-Stream Conditions and Surface Roughness.
Beyak, Ethan S.
Groot, Koen J.
and
Reed, Helen L.
2021.
Computational Stability Analysis of a Variably Swept, Slotted Natural-Laminar-Flow Airfoil.
Yadala, Srikar
Hehner, Marc T.
Serpieri, Jacopo
Benard, Nicolas
and
Kotsonis, Marios
2021.
Plasma-Based Forcing Strategies for Control of Crossflow Instabilities.
AIAA Journal,
Vol. 59,
Issue. 9,
p.
3406.
Rius-Vidales, Alberto F.
and
Kotsonis, M.
2021.
Impact of a forward-facing step on the development of crossflow instability.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Raghuram, S.
and
Ramesh, O. N.
2021.
Delayed transition in a plane channel flow with high contraction ratio.
Experiments in Fluids,
Vol. 62,
Issue. 7,
Zoppini, Giulia
Ragni, Daniele
and
Kotsonis, Marios
2021.
Experimental Investigation on Receptivity of Crossflow Instability to Discrete Roughness Amplitude and Location.
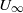 ${U}_{\infty } $. Measurements of the stationary and travelling mode amplitudes are made in the boundary layer of a 1.83 m chord,
${U}_{\infty } $. Measurements of the stationary and travelling mode amplitudes are made in the boundary layer of a 1.83 m chord, 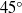 $45{{}^\circ} $ swept-wing model. These results are compared to those of similar experiments at higher turbulence levels to broaden the current knowledge of this portion of the cross-flow problem. It is observed that both free-stream turbulence and surface roughness contribute to the initiation of unsteady disturbances, and that free-stream turbulence affects the development of both stationary and unsteady cross-flow disturbances. For the range tested, enhanced free-stream turbulence advances the transition location except when a subcritically spaced roughness array is employed.
$45{{}^\circ} $ swept-wing model. These results are compared to those of similar experiments at higher turbulence levels to broaden the current knowledge of this portion of the cross-flow problem. It is observed that both free-stream turbulence and surface roughness contribute to the initiation of unsteady disturbances, and that free-stream turbulence affects the development of both stationary and unsteady cross-flow disturbances. For the range tested, enhanced free-stream turbulence advances the transition location except when a subcritically spaced roughness array is employed.