Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T22:11:15.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-surface disturbances due to the submersion of a cylindrical obstacle

Published online by Cambridge University Press:  06 September 2021

R. Martín Pardo Open the ORCID record for R. Martín Pardo [Opens in a new window]  and
J. Nedić Open the ORCID record for J. Nedić [Opens in a new window]
R. Martín Pardo*
Affiliation:
Department of Mechanical Engineering, McGill University, Montréal, QCH3A 0G4, Canada
J. Nedić*
Affiliation:
Department of Mechanical Engineering, McGill University, Montréal, QCH3A 0G4, Canada
*
†Email addresses for correspondence: rubert.martin@mail.mcgill.ca, jovan.nedic@mail.mcgill.ca
†Email addresses for correspondence: rubert.martin@mail.mcgill.ca, jovan.nedic@mail.mcgill.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

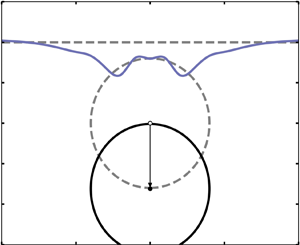
We explore the initial perturbations that form on a liquid free surface as a result of the submersion of a circular cylinder beneath the surface, a scenario that arises in a number of diverse applications. The behaviour of the free surface is determined by transforming the equations of motion of the system via the Wehausen scheme, to variables for the free surface. A small-time series expansion is utilized to construct a recursive scheme that can be implemented numerically, and the time frame over which this approximation is valid is analysed. The resulting numerical model allows one to extend the results in the literature to study arbitrary cylinder sizes, including those where the cylinder is close to the free surface, and arbitrary cylinder motions. Of particular interest in this study was identifying the conditions under which strong jets would appear, and those were the free surface exhibited gravity waves. The formation of a central jet is found to be related to the growth of secondary, nonlinear waves, which rapidly merge as the obstacle is submerged. Classification maps are presented as a function of obstacle size and submersion speed, to identify the conditions which lead to jetting. Furthermore, the acceleration profile of the cylinder is shown to significantly affect the conditions under which jets form, which we argue is due to the rate at which energy is injected into the system.

JFM classification

Instability: Nonlinear instability Waves/Free-surface Flows: Surface gravity waves Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 926 , 10 November 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Atkinson, K.E. & Shampine, L.F. 2008 Algorithm 876: solving fredholm integral equations of the second kind in MATLAB. ACM Trans. Math. Softw. 34 (4), 21.CrossRefGoogle Scholar
Eggers, J. & Dupont, T.F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71 (3).CrossRefGoogle Scholar
Greenhow, M. 1988 Water-entry and-exit of a horizontal circular cylinder. Appl. Ocean Res. 10 (4), 191–198.CrossRefGoogle Scholar
Greenhow, M. & Lin, W.M. 1983 Nonlinear-free surface effects: experiments and theory. Tech. Rep. 83–19. MIT.Google Scholar
Greenhow, M. & Moyo, S. 1997 Water entry and exit of horizontal circular cylinders. Phil. Trans. R. Soc. Lond. A 355 (1724), 551–563.CrossRefGoogle Scholar
Guerber, E., Benoit, M., Grilli, S. & Buvat, C. 2012 A fully nonlinear implicit model for wave interactions with submerged structures in forced or free motion. Engng Anal. Bound. Elem. 36 (7), 1151–1163.CrossRefGoogle Scholar
Havelock, T.H. 1927 The method of images in some problems of surface waves. Proc. R. Soc. Lond. A 115 (771), 268–280.Google Scholar
Havelock, T.H. 1936 The forces on a circular cylinder submerged in a uniform stream. Proc. R. Soc. Lond. A 157 (892), 526–534.Google Scholar
Howell, P.D. 2015 Models for thin viscous sheets. Eur. J. Appl. Maths 7 (September 2008), 321–343.CrossRefGoogle Scholar
Huneault, J., Plant, D. & Higgins, A. 2019 Rotational stabilisation of the Rayleigh–Taylor instability at the inner surface of an imploding liquid shell. J. Fluid Mech. 873, 531–567.CrossRefGoogle Scholar
Kostikov, V.K. & Makarenko, N.I. 2018 Unsteady free surface flow above a moving circular cylinder. J. Engng Maths 112 (1), 1–16.CrossRefGoogle Scholar
Lamb, H. 1913 On some cases of wave-motion on deep water. Annali di Matematica Pura ed Applicata 21 (1), 237–250.CrossRefGoogle Scholar
Makarenko, N.I. 2003 Nonlinear interaction of submerged cylinder with free surface. Trans. ASME J. Offshore Mech. Arctic Engng 125 (1), 72–75.CrossRefGoogle Scholar
McCauley, G., Wolgamot, H., Orszaghova, J. & Draper, S. 2018 Linear hydrodynamic modelling of arrays of submerged oscillating cylinders. Appl. Ocean Res. 81, 1–14.CrossRefGoogle Scholar
Moreira, R.M. & Peregrine, D.H. 2010 Nonlinear interactions between a free-surface flow with surface tension and a submerged cylinder. J. Fluid Mech. 648, 485–507.CrossRefGoogle Scholar
Orszaghova, J., Wolgamot, H., Draper, S., Eatock Taylor, R., Taylor, P.H. & Rafiee, A. 2019 Transverse motion instability of a submerged moored buoy. Proc. R. Soc. Lond. A 475 (2221), 20180459.Google Scholar
Ovsyannikov, L.V., Makarenko, N.I., Nalimov, V.I., Liapidevskii, V.Y., Plotnikov, P.I., Sturova, I.V., Bukreev, V.I. & Vladimirov, V.A. 1985 Nonlinear Problems of the Theory of Surface and Internal Waves. Nauka.Google Scholar
Pyatkina, E.V. 2003 Small-time expansion of wave motion generated by a submerged sphere. J. Appl. Mech. Tech. Phys. 44 (1), 32–43.CrossRefGoogle Scholar
Rein, M. 1996 The transitional regime between coalescing and splashing drops. J. Fluid Mech. 306, 145–165.CrossRefGoogle Scholar
Siddorn, P. & Eatock Taylor, R. 2008 Diffraction and independent radiation by an array of floating cylinders. Ocean Engng 35 (13), 1289–1303.CrossRefGoogle Scholar
Teles da Silva, A.F. & Peregrine, D.H. 1990 Nonlinear perturbations on a free surface induced by a submerged body: a boundary integral approach. Engng Anal. Bound. Elem. 7 (4), 214–222.CrossRefGoogle Scholar
Telste, J.G. 1986 Inviscid flow about a cylinder rising to a free surface. J. Fluid Mech. 182, 149–168.CrossRefGoogle Scholar
Terent'ev, A.G. 1991 Nonstationary motion of bodies in a fluid. Proc. Steklov Znst. Maths 186, 211–221.Google Scholar
Tuck, E.O. 1965 The effect of non-linearity at the free surface on flow past a submerged cylinder. J. Fluid Mech. 22 (2), 401–414.CrossRefGoogle Scholar
Tyvand, P. & Miloh, T. 1995 Free-surface flow due to impulsive motion of a submerged circular cylinder. J. Fluid Mech. 286, 67–101.CrossRefGoogle Scholar
Wehausen, J.V. & Laitone, E.V. 1960 Surface Waves. In Fluid Dynamics/Strömungsmechanik, pp. 446–778. Springer.CrossRefGoogle Scholar
Zhao, H., Brunsvold, A. & Munkejord, S.T. 2011 Investigation of droplets impinging on a deep pool: transition from coalescence to jetting. Exp. Fluids 50 (3), 621–635.CrossRefGoogle Scholar