Article contents
General solutions of linear poro-viscoelastic materials in spherical coordinates
Published online by Cambridge University Press: 04 August 2022
Abstract
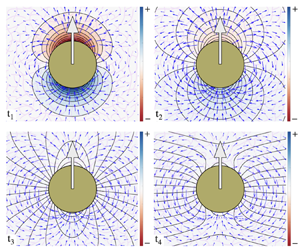
The cell cytoskeleton is a dynamic assembly of semi-flexible filaments and motor proteins. The cytoskeleton mechanics is a determining factor in many cellular processes, including cell division, cell motility and migration, mechanotransduction and intracellular transport. Mechanical properties of the cell, which are determined partly by its cytoskeleton, are also used as biomarkers for disease diagnosis and cell sorting. Experimental studies suggest that in whole cell scale, the cell cytoskeleton and its permeating cytosol may be modelled as a two-phase poro-viscoelastic (PVE) material composed of a viscoelastic (VE) network permeated by a viscous cytosol. We present the first general solution to this two-phase system in spherical coordinates, where we assume that both the fluid and network phases are in their linear response regime. Specifically, we use generalized linear incompressible and compressible VE constitutive equations to describe the stress in the fluid and network phases, respectively. We assume a constant permeability that couples the fluid and network displacements. We use these general solutions to study the motion of a rigid sphere moving under a constant force inside a two-phase system, composed of a linear elastic network and a Newtonian fluid. It is shown that the network compressibility introduces a slow relaxation of the sphere and non-monotonic network displacements with time along the direction of the applied force. Our results can be applied to particle-tracking microrheology to differentiate between PVE and VE materials, and to measure the fluid permeability as well as VE properties of the fluid and the network phases.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


