Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T07:36:56.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised solutions to the Benjamin problem

Published online by Cambridge University Press:  15 April 2020

Vladimir V. Ostapenko Open the ORCID record for Vladimir V. Ostapenko [Opens in a new window]
Vladimir V. Ostapenko*
Affiliation:
Lavrentyev Institute of Hydrodynamics of the Siberian Branch of the Russian Academy of Sciences, Lavrentyev Avenue 15, Novosibirsk, 630090, Russia Novosibirsk State University, Pirogova street 2, Novosibirsk, 630090, Russia
*
†Email address for correspondence: ostigil@mail.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

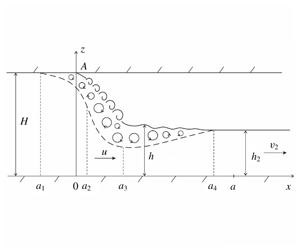
We generalise the classical Benjamin solution (Benjamin, J. Fluid Mech., vol. 31, 1968, pp. 209–248) modelling the flow in a horizontal duct of finite depth in situations where the flow contains a region spanning the depth of the duct, and a region in which the surface detaches from the ceiling of the duct as a free surface. It is shown that the Benjamin solution belongs to a one-parameter family of similar solutions, which are divided into two types: solutions that describe potential flows where the free surface of the fluid is deflected from the duct ceiling at a zero angle; and solutions that admit the formation of a vortex flow region in the vicinity of the point of fluid separation from the duct ceiling. It is shown that this one-parameter family of solutions is the limit of a two-parameter family of solutions in which part of the uniform flow energy is converted into energy of the small-scale fluid motion. Based on the local hydrostatic approximation, the applicability of the constructed solutions is discussed.

JFM classification

Waves/Free-surface Flows: Channel flow Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , R1
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atrabi, H. B., Asce, S. M., Hosoda, T. & Tada, A. 2015 Simulation of air cavity advancing into a straight duct. J. Hydraul. Engng 141, 04014068.Google Scholar
Baines, P. G. 2016 Internal hydraulic jumps in two-layer systems. J. Fluid Mech. 787, 1–15.CrossRefGoogle Scholar
Baines, W. D. & Wilkinson, D. L. 1986 The motion of large air bubbles in ducts of moderate slope. J. Hydraul Res. 25, 157–170.Google Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Borden, Z. & Meiburg, E. 2013 Circulation-based models for Boussinesq internal bores. J. Fluid Mech. 726, R1.CrossRefGoogle Scholar
Clancy, L. J. 1975 Aerodynamics. Pitman.Google Scholar
Friedrichs, K. O. 1948 On the derivation of shallow water theory. J. Fluid Mech. 1, 109–134.Google Scholar
Friedrichs, K. O. & Lax, P. D. 1971 Systems of conservation equation with convex extension. Proc. Natl Acad. Sci. USA 68, 1686–1688.CrossRefGoogle Scholar
Hager, W. H. 1999 Cavity outflow from a nearly horizontal pipe. Intl J. Multiphase Flow 25, 349–364.CrossRefGoogle Scholar
Konopliv, N. A., Smith, S. G., McElwaine, J. N. & Meiburg, E. 2016 Modelling gravity currents without an energy closure. J. Fluid Mech. 789, 806–829.CrossRefGoogle Scholar
Korobkin, A. A. 2013 A linearized model of water exit. J. Fluid Mech. 737, 368–386.CrossRefGoogle Scholar
Lax, P. D. 1972 Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves. Society for Industrial and Applied Mathematics.Google Scholar
Ostapenko, V. V. 2018 Justification of shallow-water theory. Dokl. Phys. 63, 33–37.CrossRefGoogle Scholar
Ostapenko, V. V. & Kovyrkina, O. A. 2017 Wave flows induced by lifting of a rectangular beam partly immersed in shallow water. J. Fluid Mech. 816, 442–467.CrossRefGoogle Scholar
Plotnikov, P. I. & Toland, J. F. 2004 Convexity of Stokes waves of extreme form. Arch. Rat. Mech. Anal. 171, 349–416.CrossRefGoogle Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Stocker, J. J. 1957 Water Waves: the Mathematical Theory with Applications. Wiley.Google Scholar
Sundquist, M. J. & Papadakis, C. N. 1983 Surging in combined free surface-pressurized systems. J. Transp. Eng. 109, 232–245.CrossRefGoogle Scholar
Ungarish, M. 2010 Energy balances for gravity currents with a jump at the interface produced by lock release. Acta Mechanica 211, 1–21.CrossRefGoogle Scholar
Wallis, G. B., Crowley, C. J. & Hagi, Y. 1977 Conditions for a pipe to run full when discharging liquid into a space filled with gas. Trans. ASME J. Fluids Engng 99, 405–413.CrossRefGoogle Scholar
Wilkinson, D. L. 1982 Motion of air cavities in long horizontal ducts. J. Fluid Mech. 118, 109–122.CrossRefGoogle Scholar